Polynomial magic III : Hermite polynomials

After two blog posts earlier this year on Chebyshev and Jacobi polynomials, I am coming back to orthogonal polynomials, with Hermite polynomials.

This time, in terms of applications to machine learning, no acceleration, but some interesting closed-form expansions in positive-definite kernel methods.

Definition and first properties

There are many equivalent ways to define Hermite polynomials. A natural one is through the so-called Rodrigues’ formula: $$H_k(x) = (-1)^k e^{x^2} \frac{d^k}{d x^k}\big[ e^{-x^2} \big],$$ from which we can deduce \(H_0(x) = 1\), \(H_1(x) =\ – e^{x^2} \big[ -2x e^{-x^2} \big] = 2x\), \(H_2(x) = e^{x^2} \big[ (-2x)^2e^{-x^2} -2 e^{-x^2} \big] = 4x^2 – 2\), etc.

Other simple properties which are consequences of the definition (and can be shown by recursion) are that \(H_k\) is a polynomial of degree \(k\), with the same parity as \(k\), and with a leading coefficient equal to \(2^k\).

Orthogonality for Gaussian distribution. Using integration by parts, one can show (see end of the post) that for \(k \neq \ell\), we have $$\int_{-\infty}^{+\infty} \!\!\!H_k(x) H_\ell(x) e^{-x^2} dx =0, $$ and that for \(k=\ell\), we have $$\int_{-\infty}^{+\infty} \!\!\! H_k(x)^2 e^{-x^2}dx = \sqrt{\pi} 2^k k!.$$

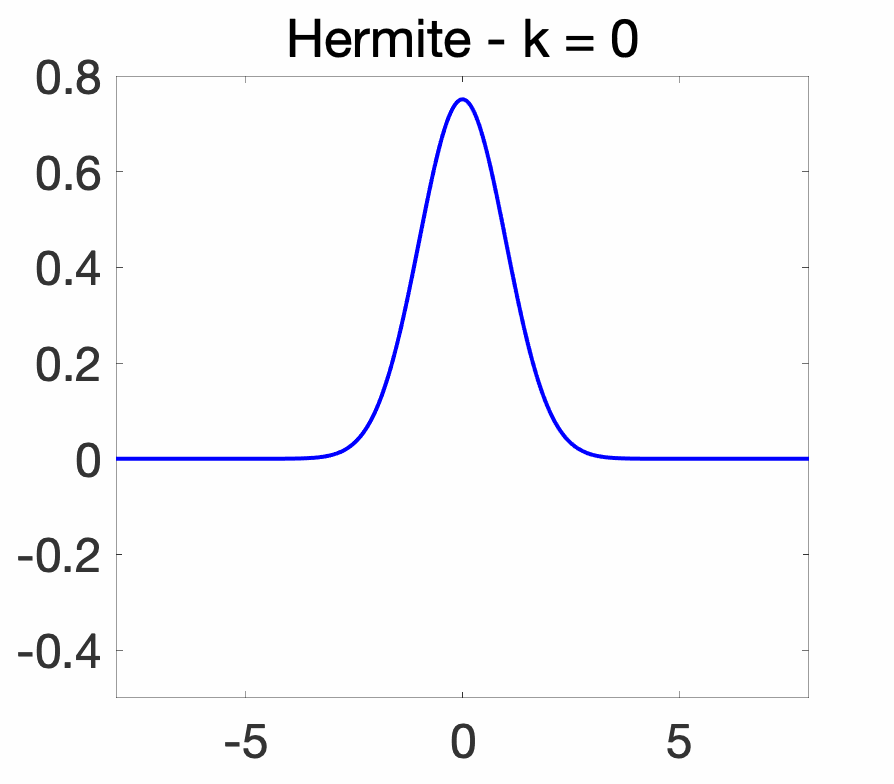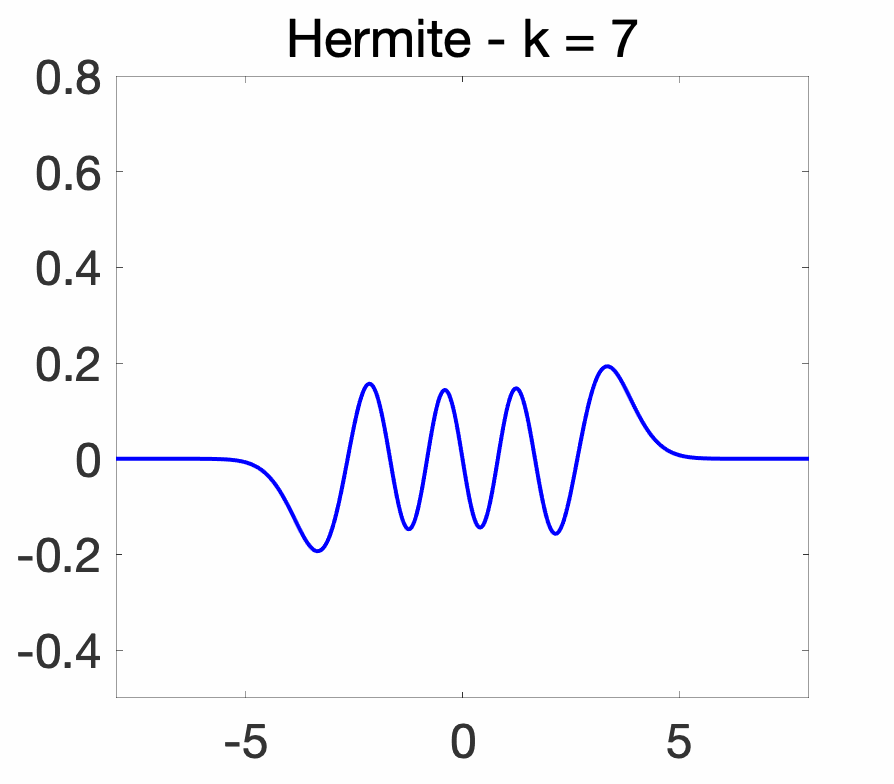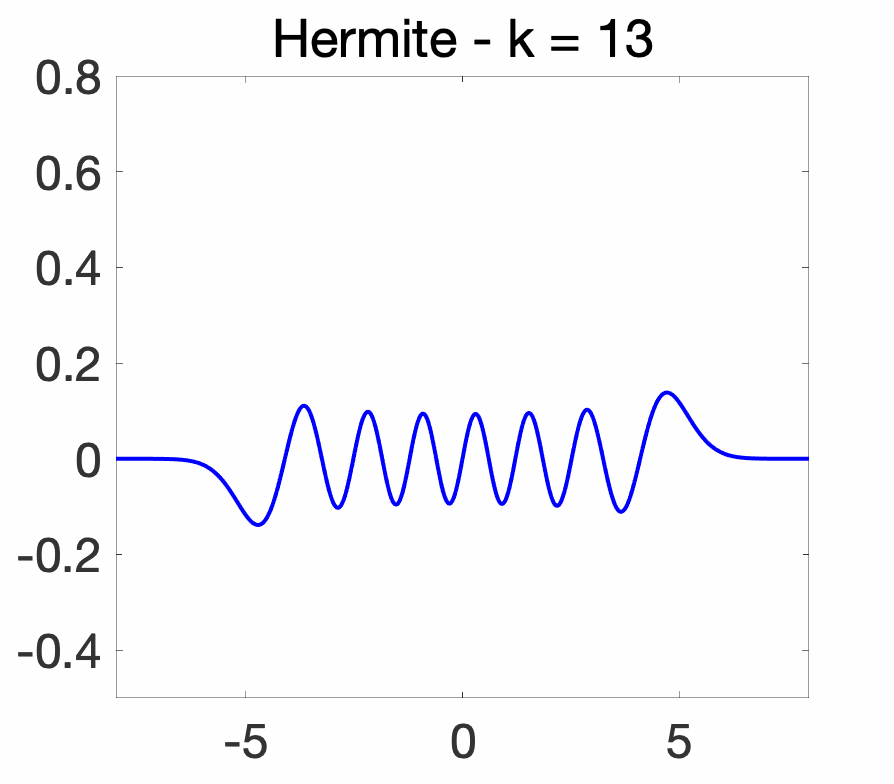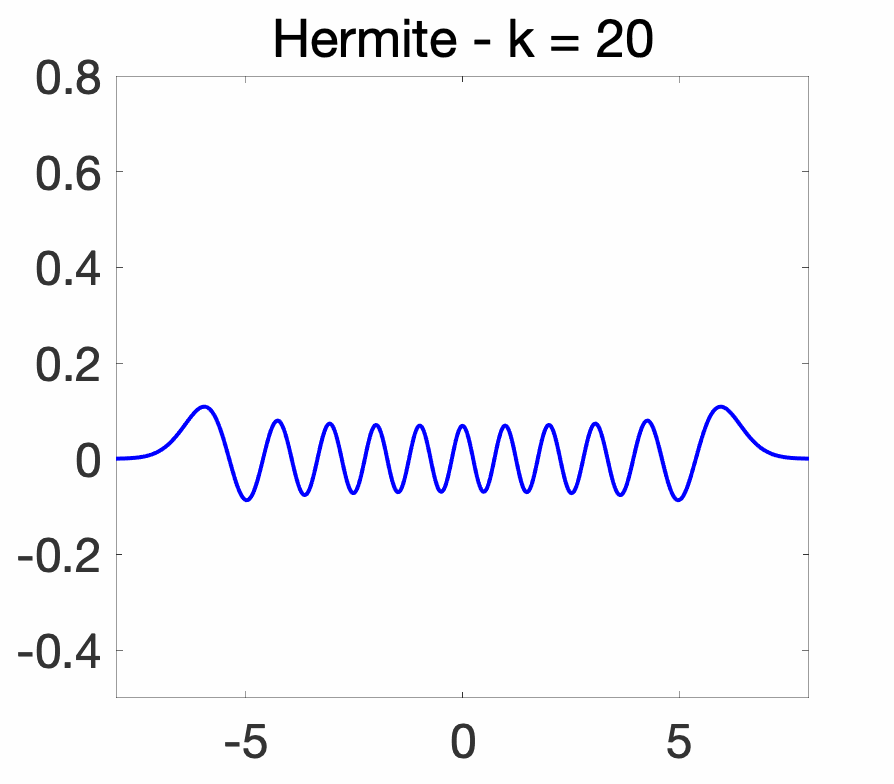
In other words, the Hermite polynomials are orthogonal for the Gaussian distribution with mean \(0\) and variance \(\frac{1}{2}\). Yet in other words, defining the Hermite functions as \( \displaystyle \psi_k(x) = (\sqrt{\pi} 2^k k!)^{-1/2} H_k(x) e^{-x^2/2}\), we obtain an orthonormal basis of \(L_2(dx)\). As illustrated below, the Hermite functions, as the index \(k\) increases, have an increasing “support” (the support is always the entire real line, but most of the mass is concentrated in centered balls of increasing sizes, essentially at \(\sqrt{k}\)) and, like cosines and sines, an increasingly oscillatory behavior.

Among such orthonormal bases, the Hermite functions happen to be diagonalizing the Fourier tranform operator. In other words, the Fourier transform of \(\psi_k\) (for the definition making it an isometry of \(L_2(dx)\)) is equal to $$ \mathcal{F}(\psi_k)(\omega)  = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} \psi_k(x) e^{- i \omega x} dx = (-i)^k \psi_k(\omega).$$ (note that the eigenvalues are all of unit modulus as we have an isometry). See a proof at the end of the post. I am not aware of any applications of this property in machine learning or statistics (but there are probably some).

Recurrence. In order to compute Hermite polynomials, the following recurrence relation is the most useful $$ H_{k+1}(x) = 2x H_k(x) \ – 2k H_{k-1}(x). \tag{1}$$ Such recursions are always available for orthogonal polynomials (see [4]), but it takes here a particularly simple form (see a proof at the end of the post).

Generating function. The following property is central in many proofs of properties of Hermite polynomials: for all \(t \in \mathbb{R}\), we have $$\sum_{k=0}^\infty \frac{t^k}{k!} H_k(x) =e^{ 2xt \ – \ t^2}, \tag{2}$$ with a proof at the end of the post based on the residue theorem.

Further (less standard) properties

For the later developments, we need other properties which are less standard (there are many other interesting properties, which are not useful for this post, see here).

Mehler formula. For \(|\rho| < 1\), it states: $$ \exp \Big( – \frac{\rho}{1- \rho^2} (x-y)^2\Big) = \sqrt{1-\rho^2} \sum_{k=0}^\infty \frac{\rho^k}{2^k k!} H_k(x) H_k(y) \exp \Big( – \frac{\rho}{1+\rho} (x^2 + y^2) \Big).$$ The proof is significantly more involved; see [1] for details (with a great last sentence: “Prof. Hardy tells me that he has not seen his proof in print, though the inevitability of the successive steps makes him think that it is unlikely to be new”). Note that we will in fact obtain a new proof from the relationship with kernel methods (see below).

Expectation for Gaussian distributions. We will need this property for \(|\rho|<1\) (see proof at the end of the post), which corresponds to the expectation of \(H_k(x)\) for \(x\) distributed as a non-centered Gaussian distribution: $$\int_{-\infty}^\infty H_k(x) \exp\Big( – \frac{(x-\rho y)^2}{1-\rho^2} \Big)dx= \sqrt{\pi} \rho^k \sqrt{1-\rho^2} H_k (y). \tag{3}$$

Given the relationship with the Gaussian distribution, it is no surprise that Hermite polynomials pop up whenever Gaussians are used, as distributions or kernels. Before looking into it, let’s first give a brief review of kernel methods.

From positive-definite kernel to Hilbert spaces

Given a prediction problem with inputs in a set \(\mathcal{X}\), a traditional way of parameterizing real-valued functions on \(\mathcal{X}\) is to use positive-definite kernels.

A positive-definite kernel is a function \(K: \mathcal{X} \times \mathcal{X} \to \mathbb{R}\) such that for all sets \(\{x_1,\dots,x_n\}\) of \(n\) elements of \(\mathcal{X}\), the “kernel matrix” in \(\mathbb{R}^{n \times n}\) composed of pairwise evaluations is symmetric positive semi-definite. This property happens to be equivalent to the existence of a Hilbert feature space \(\mathcal{H}\) and a feature map \(\varphi: \mathcal{X} \to \mathcal{H}\) such that $$K(x,x’) = \langle \varphi(x), \varphi(x’) \rangle_{\mathcal{H}},$$ with an elegant constructive proof [15].

This allows to define the space of linear functions on the features, that is, functions of the form $$f(x) = \langle f, \varphi(x) \rangle_{\mathcal{H}},$$ for \(f \in \mathcal{H}\).

This space is often called the reproducing kernel Hilbert space (RKHS) associated to the kernel \(K\) (we can prove that it is indeed uniquely defined). In such a space, we can also define the squared norm of the function \(f\), namely \(\| f\|_{\mathcal{H}}^2\), which can be seen as a specific regularization term in kernel methods.

The space satisfies the so-called reproducing property (hence its name): \(f(x) = \langle f, K(\cdot,x) \rangle_{\mathcal{H}}\). In other words, the feature \(\varphi(x)\) is the kernel function evaluated at \(x\), that is, \(\varphi(x) = K(\cdot,x)\). These spaces have been a source of many developments in statistics [5] and machine learning [6, 7].

Orthonormal basis. A difficulty in working with infinite-dimensional Hilbert spaces of functions is that it is sometimes hard to understand what functions are actually considered. One simple way to enhance understanding of the regularization property is to have an orthonormal basis (in very much the same way as the Fourier basis), as we can then identify \(\mathcal{H}\) to the space of squared-integrable sequences.

For kernel-based Hilbert spaces, if we have an orthonormal basis \((g_k)_{k \geqslant 0}\) of the Hilbert space \(\mathcal{H}\), then, by decomposing \(\varphi(x)\) in the basis, we have $$\varphi(x) = \sum_{k =0}^\infty \langle \varphi(x), g_k \rangle_\mathcal{H} g_k,$$ we get $$K(x,y) = \langle \varphi(y), \varphi(x) \rangle = \sum_{k =0}^\infty \langle \varphi(x), g_k \rangle_\mathcal{H} \langle \varphi(y), g_k \rangle_\mathcal{H} =\sum_{k=0}^\infty g_k(x) g_k(y), \tag{4}$$ that is, we have an expansion of the kernel as an infinite sum (note here, that we ignore summability issues).

Among orthonormal bases, some are more interesting than others. The ones composed of eigenfunctions for particular operators are really more interesting, in particular for the covariance operator that we now present, and their use in statistical learning theory.

Analyzing ridge regression through covariance operators

The most classical problem where regularization by RKHS norms occurs is ridge regression, where, given some observations \((x_1,y_1),\dots,(x_n,y_n) \in \mathcal{X} \times \mathbb{R}\), one minimizes with respect to \(f \in \mathcal{H}\): $$ \frac{1}{n} \sum_{i=1}^n \big( y_i \ – \langle f, \varphi(x_i) \rangle_{\mathcal{H}} \big)^2 + \lambda \| f\|_{\mathcal{H}}^2.$$

In finite dimensions, the convergence properties are characterized by the (non-centered) covariance matrix \(\Sigma = \mathbb{E} \big[ \varphi(x) \otimes \varphi(x) \big]\), where the expectation is taken with respect to the underlying distribution of the observations \(x_1,\dots,x_n\) (which are assumed independently and identically distributed for simplicity). If \(\mathcal{H} = \mathbb{R}^d\), then \(\Sigma\) is a \(d \times d\) matrix.

For infinite-dimensional \(\mathcal{H}\), the same expression \(\Sigma = \mathbb{E} \big[ \varphi(x) \otimes \varphi(x) \big]\) defines a linear operator from \(\mathcal{H}\) to \(\mathcal{H}\), so that for \(f,g \in \mathcal{H}\), we have $$\langle f, \Sigma g \rangle_{\mathcal{H}} = \mathbb{E} \big[ \langle f, \varphi(x)\rangle_{\mathcal{H}}\langle g, \varphi(x)\rangle_{\mathcal{H}}\big] = \mathbb{E} \big[ f(x) g(x) \big].$$

The generalization property of ridge regression has been thoroughly studied (see, e.g., [8, 9]), and if there exists \(f_\ast \in \mathcal{H}\) such that \(y_i = \langle f_\ast, \varphi(x_i) \rangle + \varepsilon_i\) for a noise \(\varepsilon_i\) which is independent of \(x_i\), with zero mean and variance equal to \(\sigma^2\), then the expected error on unseen data is asymptotically upper-bounded by $$\sigma^2 + \lambda \| f_\ast\|_{\mathcal{H}}^2 + \frac{\sigma^2}{n} {\rm tr} \big[ \Sigma ( \Sigma + \lambda I)^{-1} \big].$$ The first term \(\sigma^2\) is the best possible expected performance, the term \(\lambda \| f_\ast\|_{\mathcal{H}}^2\) is usually referred to as the bias term and characterizes the bias introduced by regularizing towards zero, while the third term \(\frac{\sigma^2}{n} {\rm tr} \big[ \Sigma ( \Sigma + \lambda I)^{-1} \big]\) is the variance term, which characterizes the loss in performance due to the observation of only \(n\) observations.

The quantity \({\rm df}(\lambda) = {\rm tr} \big[ \Sigma ( \Sigma + \lambda I)^{-1} \big]\) is often referred to as the degrees of freedom [10]. When \(\lambda\) tends to infinity, then \({\rm df}(\lambda)\) tends to zero; when \(\lambda\) tends to zero, then \({\rm df}(\lambda)\) tends to the number of non-zero eigenvalues of \(\Sigma\). Thus, in finite dimension, this typically leads to the underlying dimension. Given the usual variance term in \(\sigma^2 \frac{d}{n}\) for ordinary least-squares with \(d\)-dimensional features, \({\rm df}(\lambda)\) is often seen as an implicit number of parameters for kernel ridge regression.

In infinite dimensions, under mild assumptions, there are infinitely many eigenvalues for \(\Sigma\), which form a decreasing sequence \((\lambda_i)_{i \geqslant 0}\) that tends to zero (and is summable, with a sum equal to the trace of \(\Sigma\)). The rate of such a decay is key to understanding the generalization capabilities of kernel methods. With the following classical types of decays:

• Polynomial decays: If \(\lambda_i \leqslant \frac{C}{(i+1)^{\alpha}}\) for \(\alpha > 1\), then one can upper bound the sum by an integral as $$ {\rm tr} \big[ \Sigma ( \Sigma + \lambda I)^{-1} \big] = \sum_{i=0}^\infty \frac{\lambda_i}{\lambda_i + \lambda} \leqslant \sum_{i=1}^\infty \frac{1}{1 + \lambda i^\alpha / C} \leqslant \int_0^\infty \frac{1}{1+\lambda t^\alpha / C} dt.$$ With the change of variable \(u = \lambda t^\alpha / C\), we get that \({\rm df}(\lambda) = O(\lambda^{-\alpha})\). We can then balance bias and variance with \(\lambda \sim n^{-\alpha/(\alpha+1)}\) and an excess risk proportional to \(n^{-\alpha/(\alpha+1)}\). This type of decay is typical of Sobolev spaces.
• Exponential decays: If \(\lambda_i \leqslant {C}e^{-\alpha i}\), for some \(\alpha >0\), we have $$ {\rm tr} \big[ \Sigma ( \Sigma + \lambda I)^{-1} \big] \leqslant \sum_{i=0}^\infty \frac{{C}e^{-\alpha i}}{ \lambda + {C}e^{-\alpha i}} \leqslant \int_{0}^\infty \frac{{C}e^{-\alpha t}}{ \lambda + {C}e^{-\alpha t}}dt.$$ With the change of variable \(u = e^{-\alpha t}\), we get an upper bound $$\int_{0}^1 \frac{C}{\alpha}\frac{1}{ \lambda + {C}u}du = \frac{1}{\alpha}\big[ \log(\lambda + C) \ – \log (\lambda) \big] = \frac{1}{\alpha} \log \big( 1+\frac{C}{\lambda} \big).$$ We can then balance bias and variance with \(\lambda \sim 1/n \) and an excess risk proportional to \((\log n) / n \), which is very close to the usual parametric (finite-dimensional) rate in \(O(1/n)\). We will see an example of this phenomenon for the Gaussian kernel.

In order to analyze the generalization capabilities, we consider a measure \(d \mu\) on \(\mathcal{X}\), and the following (non-centered) covariance operator defined above as $$\mathbb{E} \big[ \varphi(x) \otimes \varphi(x) \big],$$ which is now an self-adjoint operator from \(\mathcal{H}\) to \(\mathcal{H}\) with a finite trace. The traditional empirical estimator \(\hat\Sigma = \frac{1}{n} \sum_{i=1}^n \varphi(x_i) \otimes \varphi(x_i)\), whose eigenvalues are the same as the eigenvalues of \(1/n\) times the \(n \times n\) kernel matrix of pairwise kernel evaluations (see simulation below).

Characterizing eigenfunctions. If \((g_k)\) is the eigenbasis associated to the eigenfunctions of \(\Sigma\), then it has to be an orthogonal family that span the entire space \(\mathcal{H}\) and such that \(\Sigma g_k = \lambda_k g_k\). Applying it to \(\varphi(y) = K(\cdot,y)\), we get $$ \langle K(\cdot,y), \Sigma g_k \rangle_{\mathcal{H}} = \mathbb{E} \big[ K(x,y) g_k(x) \big] = \lambda_k \langle g_k, \varphi(y)\rangle_\mathcal{H} = \lambda_k g_k(y),$$ which implies that the functions also have to be eigenfunctions of the self-adjoint so-called integral operator \(T\) defined on \(L_2(d\mu)\) as \(T f(y) = \int_{\mathcal{X}} K(x,y) f(y) d\mu(y)\). Below, we will check this property. Note that this other notion of integral operator (defined on \(L_2(d\mu)\) and not in \(\mathcal{H}\)), which has the same eigenvalues and eigenfunctions, is important to deal with mis-specified models (see [9]). Note that the eigenfunctions \(g_k\) are orthogonal for both dot-products in \(L_2(d\mu)\) and \(\mathcal{H}\), but that the normalization to unit norm differs. If \(\| g_k \|_{L_2(d\mu)}=1\) for all \(k \geqslant 0\), then we have \( \| g_k \|^2_\mathcal{H}= \lambda_k^{-1} \langle g_k, \Sigma g_k \rangle_\mathcal{H} = \lambda_k^{-1}\mathbb{E} [ g_k(x)^2] =\lambda_k^{-1}\) , and thus, \(\| \lambda_k^{1/2} g_k \|_{\mathcal{H}}=1\), and we have the kernel expansion from an orthonormal basis of \(\mathcal{H}\): $$K(x,y) = \sum_{k=0}^\infty\lambda_k g_k(x) g_k(y),$$ which will lead to a new proof for Mehler formula.

Orthonormal basis for the Gaussian kernel

Hermite polynomials naturally lead to orthonormal basis of some reproducing kernel Hilbert spaces (RKHS). For simplicity, I will focus on one-dimensional problems, but this extends to higher dimension.

Translation-invariant kernels. We consider a function \(q: \mathbb{R} \to \mathbb{R}\) which is integrable, with Fourier transform (note the different normalization than before) which is defined for all \(\omega \in \mathbb{R}\) because of the integrability: $$\hat{q}(\omega) = \int_{\mathbb{R}} q(x) e^{-i \omega x} dx.$$ We consider the kernel $$K(x,y) = q(x-y).$$ It can be check that as soon as \(\hat{q}(\omega) \in \mathbb{R}_+\) for all \(\omega \in \mathbb{R}\), then the kernel \(K\) is positive-definite.

For a translation-invariant kernel, we can write using the inverse Fourier transform formula: $$K(x,y) = q(x-y) = \frac{1}{2\pi} \int_{\mathbb{R}} \hat{q}(\omega) e^{i \omega ( x- y)} d \omega = \int_{\mathbb{R}} \varphi_\omega(x)^* \varphi_\omega(y) d \omega,$$ with \(\varphi_\omega(x) = \sqrt{\hat{q}(\omega) / (2\pi) } e^{i\omega x}\). Intuitively, for a function \(f: \mathbb{R} \to \mathbb{R}\), with \(\displaystyle f(x) = \frac{1}{2\pi} \int_{\mathbb{R}} \hat{f}(\omega)e^{i\omega x} d\omega = \int_{\mathbb{R}} \frac{\hat{f}(\omega) }{\sqrt{2 \pi \hat{q}(\omega)}}\varphi_\omega(x) d\omega\), which is a “dot-product” between the family \((\varphi_\omega(x))_\omega\) and \(\Big( \frac{\hat{f}(\omega) }{\sqrt{2 \pi \hat{q}(\omega)}} \Big)_\omega\), the squared norm \(\| f\|_{\mathcal{H}}^2\) is equal to the corresponding “squared norm” of \(\Big( \frac{\hat{f}(\omega) }{\sqrt{2 \pi \hat{q}(\omega)}}\Big)_\omega\), and we thus have $$ \| f\|_{\mathcal{H}}^2 = \int_{\mathbb{R}} \Big| \frac{\hat{f}(\omega) }{\sqrt{2 \pi \hat{q}(\omega)}} \Big|^2 d\omega = \frac{1}{2\pi} \int_{\mathbb{R}} \frac{ | \hat{f}(\omega) |^2}{\hat{q}(\omega)} d\omega,$$ where \(\hat{f}\) is the Fourier transform of \(f\). While the derivation above is not rigorous, the last expression is.

In this section, I will focus on the Gaussian kernel defined as \(K(x,y) = q(x-y) = \exp \big( – \alpha ( x- y )^2 \big)\), for which \(\displaystyle \hat{q}(\omega)= \sqrt{\frac{\pi}{\alpha}} \exp\big( – \frac{\omega^2}{4 \alpha} \big)\).

Given that \(\displaystyle \frac{1}{\hat{q}(\omega)} = \sqrt{\frac{\alpha}{\pi}} \exp\big( \frac{\omega^2}{4 \alpha} \big)= \sqrt{\frac{\alpha}{\pi}} \sum_{k=0}^\infty \frac{\omega^{2k}}{(4 \alpha)^k k!} \), the penalty \(\|f\|_\mathcal{H}^2\) is a linear combination of squared \(L_2\)-norm of \(\omega^k \hat{f}(\omega)\), which is the squared \(L_2\)-norm of the \(k\)-th derivative of \(f\). Thus, functions in the RKHS are infinitely differentiable, and thus very smooth (this implies that to have the fast rate \((\log n) / n \) above, the optimal regression function has to be very smooth).

Orthonormal basis of the RKHS. As seen in Eq. (4), an expansion in an infinite sum is necessary to obtain an orthonormal basis. We have: $$K(x,y) = e^{-\alpha x^2} e^{-\alpha y^2} e^{2 \alpha x y} = e^{-\alpha x^2} e^{-\alpha y^2} \sum_{k=0}^\infty \frac{ (2\alpha)^k}{k!} x^k y^k.$$ Because of Eq. (4), with \(g_k(x) = \sqrt{ \frac{(2\alpha)^k}{k!}} x^k \exp \big( – \alpha x^2 \big)\), we have a good candidate for an orthonornal basis. Let us check that this is the case. Note that the expansion above alone cannot be used as a proof that \((g_k)\) is an orthonormal basis of \(\mathcal{H}\).

Given the function \(f_k(x) = x^k \exp \big( – \alpha x^2 \big)\), we can compute its Fourier transform as $$ \hat{f}_k(\omega) = i^{-k} ( 4 \alpha)^{-k/2} \sqrt{\frac{\pi}{\alpha}} H_k \Big( \frac{\omega}{\sqrt{4 \alpha}} \Big) \exp\big( – \frac{\omega^2}{4 \alpha} \big) .$$ Indeed, we have, from Rodrigues’ formula, $$H_k \Big( \frac{\omega}{\sqrt{4 \alpha}} \Big) \exp\big( – \frac{\omega^2}{4 \alpha} \big) =(-1)^k (4 \alpha)^{k/2} \frac{d^k}{d \omega^k}\big[ \exp\big( – \frac{\omega^2}{4 \alpha} \big) \big],$$ and thus its inverse Fourier transform is equal to \((ix)^k\) times the one of \((-1)^k (4 \alpha)^{k/2} \exp\big( – \frac{\omega^2}{4 \alpha} \big)\), which is thus equal to \((-i)^k (4 \alpha)^{k/2} \sqrt{ \alpha / \pi }e^{-\alpha x^2} \), which leads to the Fourier transform formula above.

We can now compute the RKHS dot products, to show how to obtain the orthonormal basis described in [11]. This leads to $$ \langle f_k, f_\ell \rangle = \frac{1}{2\pi} \sqrt{\frac{\pi}{\alpha}} ( 4 \alpha)^{-k/2}( 4 \alpha)^{-\ell/2} \int_{\mathbb{R}} H_k \Big( \frac{\omega}{\sqrt{4 \alpha}} \Big) H_\ell \Big( \frac{\omega}{\sqrt{4 \alpha}} \Big) \exp\big( – \frac{\omega^2}{4 \alpha} \big) d\omega,$$ which leads to, with a change of variable $$ \langle f_k, f_\ell \rangle = \frac{1}{2\pi} \sqrt{\frac{\pi}{\alpha}} ( 4 \alpha)^{-k/2}( 4 \alpha)^{-\ell/2} \sqrt{4 \alpha} \int_{\mathbb{R}} H_k (u) H_\ell (u) \exp(-u^2) du,$$ which is equal to zero if \(k \neq \ell\), and equal to \(\frac{1}{2\pi} \sqrt{\frac{\pi}{\alpha}} ( 4 \alpha)^{-k} \sqrt{4 \alpha} \sqrt{\pi} 2^k k! = ( 2 \alpha)^{-k} k!\) if \(k = \ell\). Thus the sequence \((f_k)\) is an orthogonal basis of the RKHS, and the sequence \((g_k)\) defined as \(g_k(x) = \sqrt{ \frac{(2\alpha)^k}{k!}} f_k(x)\) is an orthonormal basis of the RKHS, from which, using the expansion as in Eq. (4), we recover the expansion: $$K(x,y) = \sum_{k=0}^\infty g_k(x) g_k(y) = e^{-\alpha x^2} e^{-\alpha y^2} \sum_{k=0}^\infty \frac{ (2\alpha)^k}{k!} x^k y^k.$$

This expansion can be used to approximate the Gaussian kernel by finite-dimensional explicit feature spaces, by just keeping the first basis elements (see an application to optimal transport in [12], with an improved behavior using an adaptive low-rank approximation through the Nyström method in [13]).

Eigenfunctions for the Gaussian kernels

In order to obtain explicit formulas for the eigenvalues of the covariance operator, we need more than a mere orthonormal basis, namely an eigenbasis.

An orthogonal basis will now be constructed with arguably better properties as it is also an orthonormal basis for both the RKHS and \(L_2(d\mu)\) for a Gaussian measure, that diagonalizes the integral operator associated to this probability measure, as well as the covariance operator.

As seen above, we simply need an orthogonal family \((f_k)_{k \geqslant 0}\), such that given a distribution \(d\mu\), \((f_k)_{k \geqslant 0}\) is a family in \(L_2(d\mu)\) such that $$\int_{\mathbb{R}} f_k(x) K(x,y) d\mu(x) = \lambda_k f_k(y), \tag{5}$$ for eigenvalues \((\lambda_k)\). In the next paragraph, we will do exactly this for the Gaussian kernel \(K(x,y) = e^{-\alpha (x-y)^2}\) for \(\alpha = \frac{\rho}{1- \rho^2}\) for some \(\rho \in (0,1)\); this particular parameterization in \(\rho\) is to make the formulas below not (too) complicated.

With \(f_k(x) = \frac{1}{\sqrt{N_k}} H_k(x) \exp \Big( – \frac{\rho}{1+\rho} x^2 \Big)\), where \(N_k = {2^k k!} \sqrt{ \frac{1-\rho}{1+\rho}}\), then \((f_k)_{k \geqslant 0}\) is an orthonormal basis for \(L_2(d\mu)\) for \(d\mu\) the Gaussian distribution with mean zero and variance \(\frac{1}{2} \frac{1+\rho}{1-\rho}\) (this is a direct consequence of the orthogonality property of Hermite polynomials).

Moreover, the moment of the Hermite polynomial in Eq. (3) exactly leads to Eq. (5) for the chosen kernel and \(\lambda_k = (1-\rho) \rho^k\). Since the eigenvalues sum to one, and the trace of \(\Sigma\) is equal to one (as a consequence of \(K(x,x)=1\)), the family \((f_k)\) has to be a basis of \(\mathcal{H}\).

From properties of the eigenbasis, since \((f_k)\) is an orthonormal eigenbasis of \(L_2(d\mu)\) and the eigenvalues are \(\lambda_k = (1-\rho)\rho^k\), we get: $$ K(x,y) = \exp \Big( – \frac{\rho}{1- \rho^2} (x-y)^2\Big) = \sum_{k=0}^\infty (1-\rho)\rho^k f_k(x) f_k(y),$$ which is exactly the Mehler formula, and thus we obtain an alternative proof.

We then get an explicit basis and the exponential decay of eigenvalues, which was first outlined by [2]. See an application to the estimation of the Poincaré constant in [14] (probably a topic for another post in a few months).

Experiments. In order to showcase the exact eigenvalues of the expectation \(\Sigma\) (for the correct combination of Gaussian kernel and Gaussian distribution), we compare the eigenvalues with the ones of the empirical covariance operator \(\hat\Sigma\), for various values of the number of observations. We see that as \(n\) increases, the empirical eigenvalues match the exact ones for higher \(k\).

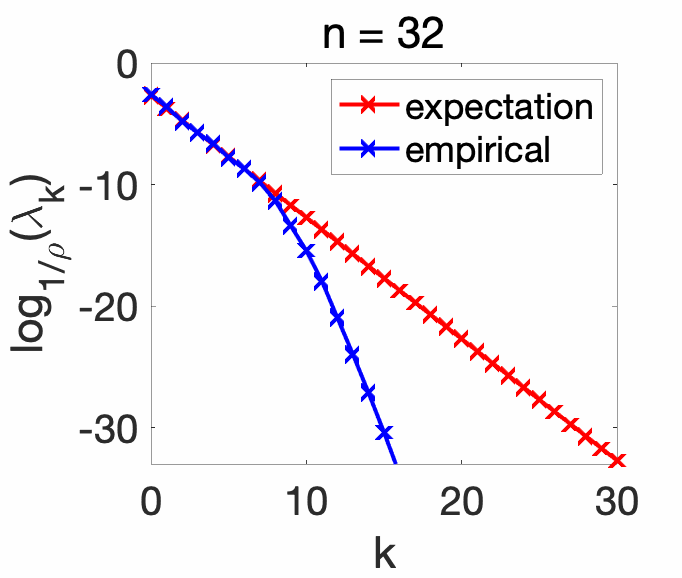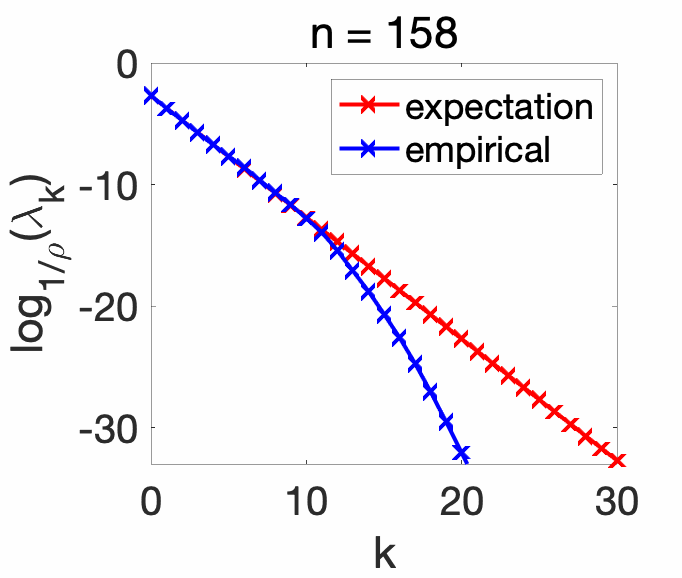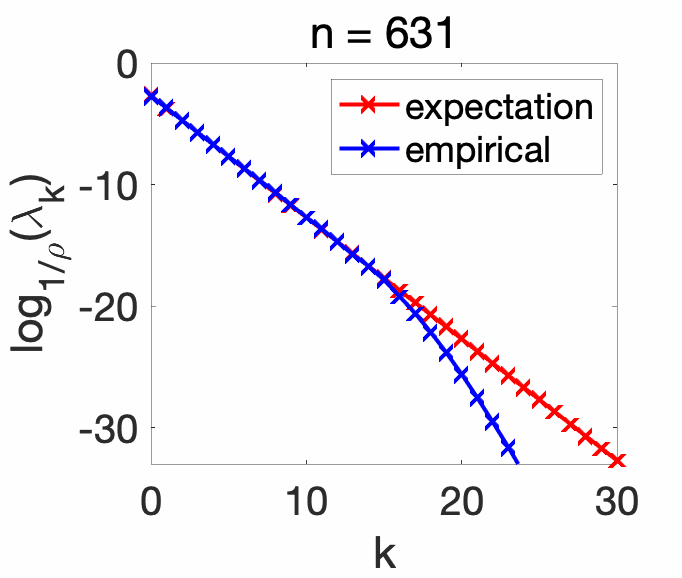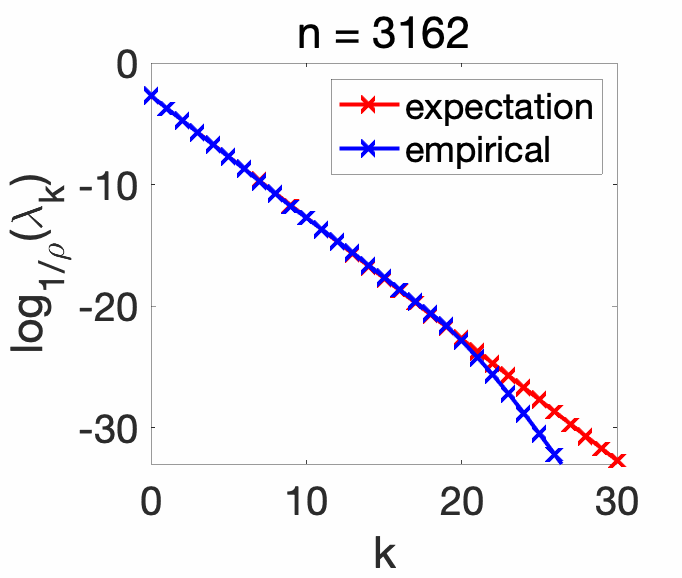
Conclusion

In this post, I only presented applications of Hermite polynomials to the Gaussian kernel, but these polynomials appear in many other areas of applied mathematics, for other types of kernels within machine learning such as dot-product kernels [3], in random matrix theory (see here), in statistics for Edgeworth expansions, and of course for Gauss-Hermite quadrature.

Acknowledgements. I would like to thank Loucas Pillaud-Vivien and Alessandro Rudi for proofreading this blog post and making good clarifying suggestions.

References

[1] George Neville Watson. Notes on Generating Functions of Polynomials: (2) Hermite Polynomials. Journal of the London Mathematical Society, 8, 194-199, 1933.
[2] Huaiyu Zhu, Christopher K. I. Williams, Richard Rohwer, and Michal Morciniec. Gaussian regression and optimal finite dimensional linear models. In Neural Networks and Machine Learning. Springer-Verlag, 1998.
[3] A. Daniely, R. Frostig, and Y. Singer. Toward deeper understanding of neural networks: The power of initialization and a dual view on expressivity. In Advances In Neural Information Processing Systems, 2016.
[4] Gabor Szegö. Orthogonal polynomials. American Mathematical Society, 1939.
[5] Grace Wahba. Spline models for observational data. Society for Industrial and Applied Mathematics, 1990.
[6] Bernhard Schölkopf, Alexander J. Smola. Learning with kernels: support vector machines, regularization, optimization, and beyond. MIT Press, 2002.
[7] John Shawe-Taylor, Nello Cristianini. Kernel methods for pattern analysis. Cambridge University Press, 2004.
[8] Andrea Caponnetto, Ernesto De Vito. Optimal rates for the regularized least-squares algorithm. Foundations of Computational Mathematics 7.3: 331-368, 2007.
[9] Jerome Friedman, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. No. 10. Springer series in statistics, 2001.
[10] Trevor Hastie and Robert Tibshirani. Generalized Additive Models. Chapman & Hall, 1990.
[11] Ingo Steinwart, Don Hush, and Clint Scovel. An explicit description of the reproducing kernel Hilbert spaces of Gaussian RBF kernels. IEEE Transactions on Information Theory, 52.10:4635-4643, 2006.
[12] Jason Altschuler, Francis Bach, Alessandro Rudi, Jonathan Niles-Weed. Approximating the quadratic transportation metric in near-linear time. Technical report arXiv:1810.10046, 2018.
[13] Jason Altschuler, Francis Bach, Alessandro Rudi, Jonathan Niles-Weed. Massively scalable Sinkhorn distances via the Nyström method. Advances in Neural Information Processing Systems (NeurIPS), 2019.
[14] Loucas Pillaud-Vivien, Francis Bach, Tony Lelièvre, Alessandro Rudi, Gabriel Stoltz. Statistical Estimation of the Poincaré constant and Application to Sampling Multimodal Distributions. Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), 2020.
[15] Nachman Aronszajn. Theory of Reproducing Kernels. Transactions of the American Mathematical Society, 68(3): 337–404, 1950.

Proof of properties of Hermite polynomials

In this small appendix, I give “simple” proofs (that sometimes require knowledge of complex analysis) to the properties presented above.

Generating function. We have, using residue theory, $$H_k(x)=(-1)^k e^{x^2} \frac{d^k}{d x^k}\big[ e^{-x^2} \big] = (-1)^k \frac{k!}{2i\pi} e^{x^2} \oint_\gamma \frac{e^{-z^2}}{(z-x)^{k+1}}dz, $$ where \(\gamma\) is a contour in the complex plane around \(x\). This leads to, for any \(t\) (here, we ignore on purpose the summability issues, for more details, see [4, Section 5.5]): $$ \sum_{k=0}^\infty \frac{t^k}{k!} H_k(x) = \frac{1}{2i\pi} e^{x^2} \oint_\gamma \frac{e^{-z^2}}{z-x} \sum_{k=0}^\infty \frac{t^k} {(x-z)^{k}}dz, $$ which can be simplified using the sum of the geometric series, leading to $$\frac{1}{2i\pi} e^{x^2} \oint_\gamma \frac{e^{-z^2}}{z-x} \frac{z-x}{z-x- t} dz = \frac{1}{2i\pi} e^{x^2} \oint_\gamma \frac{e^{-z^2}} {z-x- t} dz.$$ Using the first-order residue at \(x+t\). This is thus equal to \(e^{x^2-(t+x)^2} = e^{-t^2 + 2tx}\), which is exactly the generating function statement from Eq. (2).

Orthogonality for Gaussian distribution. We can prove through integration by parts, but there is a nicer proof through the generating function. Indeed, with $$ a_{k \ell} = \int_{-\infty}^{+\infty} e^{-x^2} H_k(x) H_\ell(x) dx, $$ for \(k, \ell \geqslant 0\), we get $$\sum_{k,\ell = 0}^\infty a_{k \ell} \frac{t^k u^\ell}{k! \ell!} = \int_{-\infty}^{+\infty}e^{-x^2}\Big( \sum_{k,\ell = 0}^\infty a_{k \ell} \frac{t^k u^\ell}{k! \ell!} H_k(x) H_\ell(x) \Big) dx.$$ Using the generating function, this leads to $$\sum_{k,\ell = 0}^\infty a_{k \ell} \frac{t^k u^\ell}{k! \ell!} = \int_{-\infty}^{+\infty} e^{-x^2 + 2xu-u^2 + 2xt – t^2} dx= e^{2uv} \int_{-\infty}^{+\infty} e^{-(x-u-v)^2}dx, $$ which can be computed explicitly using normalization constants of the Gaussian distribution, as \( \sqrt{\pi} e^{2uv} = \sqrt{\pi} \sum_{k=0}^\infty \frac{ (2 u v)^k}{k!},\) leading to all desired orthogonality relationships using the uniqueness of all coefficients for factors \(t^k u^\ell\).

Recurrence relationship. Taking the derivative of the generating function with respect to \(t\), one gets \( \displaystyle (2x-2t) e^{2tx-t^2} = \sum_{k=0}^\infty \frac{t^{k-1}}{(k-1)!} H_k(x),\) which is equal to (using again the generating function) \(\displaystyle \sum_{k=0}^\infty \frac{t^{k}}{k!} 2x H_k(x) \ – \sum_{n=0}^\infty \frac{t^{k+1}}{k!} 2 H_k(x).\) By equating the coefficients for all powers of \(t\), this leads to the desired recursion in Eq. (1).

Fourier transform. Again using the generating function, written $$ e^{-x^2/2 + 2xt – t^2} = \sum_{k=0}^\infty \frac{t^k}{k!} e^{-x^2/2} H_k(x), $$ we can take Fourier transforms and use the fact that the Fourier transform of \(e^{-x^2/2}\) is itself (for the chosen normalization), and then equate coefficients for all powers of \(t\) to conclude (see more details here).

Expectation for Gaussian distributions. We finish the appendix by proving Eq. (3). We consider computing for any \(t\), $$\sum_{k=0}^\infty \rho^k \frac{t^k}{k!} H_k (y) = e^{2\rho t y – \rho^2 t^2},$$ using the generating function from Eq. (2). We then compute $$A=\int_{-\infty}^\infty \exp\Big( – \frac{(x-\rho y)^2}{1-\rho^2} \Big) \sum_{k=0}^\infty \frac{t^k}{k!} H_k(x) dx = \int_{-\infty}^\infty \exp\Big( – \frac{(x-\rho y)^2}{1-\rho^2} \Big) \exp( 2tx – t^2) dx.$$ We then use \( \frac{(x-\rho y)^2}{1-\rho^2} – 2tx + t^2 = \frac{x^2}{1-\rho^2} – \frac{2x[ t(1-\rho^2) + \rho y]}{1-\rho^2} + t^2 + \frac{\rho^2 y^2}{1-\rho^2}\), leading to $$A = \sqrt{\pi} \sqrt{1-\rho^2} \exp\Big( -t^2 – \frac{\rho^2 y^2}{1-\rho^2} +(1-\rho^2) \big( t + \frac{\rho y}{1-\rho^2} \big)^2 \Big) = \sqrt{\pi} \sqrt{1-\rho^2} e^{2\rho t y – \rho^2 t^2}.$$ By equating powers of \(t\), this leads to Eq. (3).