Integrals appear everywhere in all scientific fields, and their numerical computation is an active area of research. In the playbook of approximation techniques, my personal favorite is “la méthode de Laplace”, a must-know for students that like to cut integrals into pieces, that comes with lots of applications.
We will be concerned with integrals of the form $$I(t) = \int_K h(x) e^{ \, – \, t f(x) } dx, $$ where \(K\) is compact (bounded and closed) subset of \(\mathbb{R}^d\), and \(h\) and \(f\) are two real-valued functions defined on \(K\) such that the integral is well defined for large enough \(t \in \mathbb{R}\). The goal is to obtain an asymptotic equivalent when \(t\) tends to infinity.
Within machine learning, as explained below, this is useful where computing and approximating integrals is important. This thus comes up naturally in Bayesian inference where \(t\) will be the number of observations in a statistical model. But let’s start with presenting this neat asymptotic result that Laplace discovered for a particular one-dimensional case in 1774 [1].
Laplace approximation
Let’s first state the main result. Assume that:
- \(h\) is continuous on \(K\) and that \(f\) is twice continuously differentiable on \(K\).
- \(f\) has a strict global minimizer \(x_\ast\) on \(K\), which is in the interior of \(K\), where the gradient \(f^\prime(x_\ast)\) is thus equal to zero, and where the Hessian \(f^{\prime \prime}(x_\ast)\) is a positive definite matrix (it is always positive semi-definite because \(x_\ast\) is a local minimizer of \(f\)); moreover, \(h(x_\ast) \neq 0\).
Then, as \(t\) tends to infinity, we have the following asymptotic equivalent: $$ I(t) \sim \frac{h(x_\ast)}{\sqrt{ \det f^{\prime \prime}(x_\ast) }} \Big( \frac{2\pi}{t}\Big)^{d/2} e^{ \, – \, t f(x_\ast) }.$$
Where does it come from? The idea is quite simple: for \(t>0\), the exponential term \(e^{ \, – \, t f(x) }\) is largest when \(x\) is equal to the minimizer \(x_\ast\). Hence only contributions close to \(x_\ast\) will count in the integral. Then we can do Taylor expansions of the two functions around \(x_\ast\), as \(h(x) \approx h(x_\ast)\) and \(f(x) \approx f(x_\ast) + \frac{1}{2} ( x – x_\ast)^\top f^{\prime \prime}(x_\ast) (x-x_\ast)\), and approximate \(I(t)\) as $$ I(t) \approx \int_K h(x_\ast) \exp\Big[ – t f(x_\ast) \ – \frac{t}{2} ( x – x_\ast)^\top f^{\prime \prime}(x_\ast) (x-x_\ast)\Big] dx.$$ We can then make a change of variable \(y = \sqrt{t} f^{\prime \prime}(x_\ast)^{1/2}( x – x_\ast)\) (where \(f^{\prime \prime}(x_\ast)^{1/2}\) is the positive square root of \(f^{\prime \prime}(x_\ast)\)), to get, with the Jacobian of the transformation leading to the term \( (\det f^{\prime \prime}(x_\ast) )^{1/2} t^{d/2} \): $$I(t) \approx \frac{ h(x_\ast) e^{ \, – \, t f(x_\ast) }}{( \det f^{\prime \prime}(x_\ast) )^{1/2}t^{d/2} } \int_{\sqrt{t}f^{\prime \prime}(x_\ast)^{1/2}( K \ – x_\ast)} \!\!\! \exp\big[ – \frac{1}{2} y^\top y \big] dy.$$ Since \(x_\ast\) is in the interior of \(K\), when \(t\) tends to infinity, the set \(\sqrt{t} f^{\prime \prime}(x_\ast)^{1/2} ( K \ – x_\ast)\) tends to \(\mathbb{R}^d\) (see illustration below), and we obtain the usual Gaussian integral that leads to the normalizing constant of the Gaussian distribution, which is equal to \((2\pi)^{d/2} \).
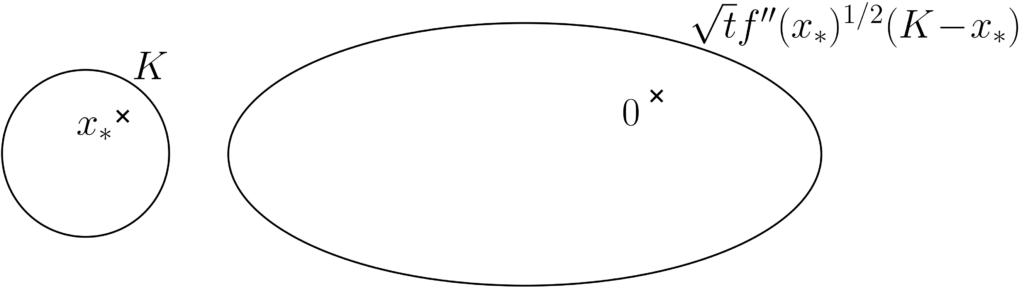
Formal proof. Let’s first make our life simpler: without loss of generality, we may assume that \(f(x_\ast) = 0\) (by subtracting the minimal value), that \(f^{\prime \prime}(x_\ast) = I\) (by a change of variable whose Jacobian is the square root of \(f^{\prime \prime}(x_\ast)\), leading to the determinant term), and that \(x_\ast = 0\). With the dominated convergence theorem (which was unfortunately unknown to me when I first learned about the method in high school, forcing students to cut integrals into multiple pieces), the proof sketch above is almost exact. We simply need a simple argument, based on the existence of a continuous function \(g: K \to \mathbb{R}\) such that $$ g(x) = \frac{f(x) } {\| x \|^2}$$ for \(x \neq 0\) and \(g(0) = \frac{1}{2}\) (here \(\| \! \cdot \! \|\) denotes the standard Euclidean norm). The function \(g\) is trivially defined and continuous on \(K \backslash \{0\}\), the value and continuity at zero is a simple consequence of the Taylor expansion $$ f(x) = f(0) + f^\prime(0)^\top x + \frac{1}{2} x^\top f^{\prime\prime}(0)x + o( \| x\|^2) = \frac{1}{2} \| x\|^2 + o( \| x\|^2). $$
We may then use the same change of variable as above to get the equality: $$I(t) = \frac{ 1 }{ t^{d/2} } \int_{\sqrt{t} K } h\big( \frac{1}{\sqrt{t}} y\big) \exp\big[ – \frac{1}{2} y^\top y \cdot g\big( \frac{1}{\sqrt{t}} y\big) \big] dy.$$ We can write the integral part of the expression above as $$J(t) = \int_{\mathbb{R}^d} a(y,t) dy, $$ with $$a(y,t) = 1_{ y \in \sqrt{t} K } h\big( \frac{1}{\sqrt{t}} y\big)\exp\big[ – \frac{1}{2} y^\top y \cdot g\big( \frac{1}{\sqrt{t}} y\big) \big].$$ We have for all \(t>0\) and \(y \in \mathbb{R}^d\), \(|a(y,t)| \leqslant \max_{z \in K} | h(z)| \exp\Big[ – \| y\|^2 \cdot \min_{ z \in K } g(z) \Big]\), which is integrable because \(h\) is continuous on the compact set \(K\) and thus bounded, and \(g\) is strictly positive on \(K\) (since \(f\) is strictly positive except at zero as \(0\) is a strict global minimum), and by continuity, its minimal value is strictly positive. Thus by the dominated convergence theorem: $$\lim_{t \to +\infty} J(t) = \int_{\mathbb{R}^d} \big( \lim_{t \to +\infty} a(y,t) \big) dy = \int_{\mathbb{R}^d}\exp\big[ – \frac{1}{2} y^\top y \big] dy = ( 2\pi)^{d/2}.$$ This leads to the desired result since \(I(t) = J(t) / t^{d/2}\).
Classical examples
Two cute examples are often mentioned as applications (adapted from [2]).
Stirling’s formula. We have, by definition of the Gamma function \(\Gamma\), and the change of variable \(u = tx\):
$$\Gamma(1+t) = \int_0^\infty \!\! e^{-u} u^{t} du = \int_0^\infty \!\! e^{-tx}t^t x^t t dx = t^{t+1} \int_0^\infty \!\! e^{-t(x-\log x)} dx.$$ Since \(x \mapsto x\, – \log x\) is minimized at \(x=1\) with second derivative equal to \(1\), we get: $$\Gamma(1+t) \sim t^{t+1} e^{-t} \sqrt{2\pi / t} = \big( \frac{t}{e} \big)^t \sqrt{ 2\pi t}.,$$ which is exactly Stirling’s formula, often used when \(t\) is an integer, and then, \(\Gamma(1+t) = t!\).
Convergence of \(L_p\)-norms to the \(L_\infty\)-norm. We consider the \(L_p\)-norm of a positive twice continuously differentiable function on the compact set \(K\), with a unique global maximizer at \(x_\ast\) in the interior of \(K\). Then we can write its \(L_p\)-norm \(\|g\|_p\) through $$\| g\|_p^p = \int_K g(x)^p dx = \int_K e^{ p \log g(x)} dx.$$ The function \(f: x \mapsto\ – \log g(x)\) has gradient \(f^\prime(x) = \ – \frac{1}{g(x)}g^\prime(x)\) and Hessian \(f^{\prime\prime}(x)=\ – \frac{1}{g(x)} g^{\prime\prime}(x) + \frac{1}{g(x)^2} g^\prime(x) g^\prime(x)^\top .\) At \(x_\ast\), we get \(f^{\prime\prime}(x_\ast) = \ – \frac{1}{g(x_\ast)} g^{\prime \prime}(x_\ast)\). Thus, using Laplace’s method, we have: $$ \|g\|_p^p = \frac{A}{p^{d/2}} g(x_\ast)^p (1 + o(1) ),$$ with \(\displaystyle A = \frac{(2\pi g(x_\ast))^{d/2}}{(\det (-g^{\prime\prime}(x_\ast)))^{1/2}}\).
Taking the power \(1/p\), we get: $$ \|g\|_p = \exp \big( \frac{1}{p} \log \|g\|_p^p\big) = \exp \Big( \frac{1}{p} \log A \ – \frac{d}{2p} \log p + \log g(x_\ast) + o(1/p) \Big).$$ This leads to, using \(\exp(u) = 1+u + o(u)\) around zero: $$ \| g\|_p = g(x_\ast) \Big( 1 – \frac{d}{2p} \log p + \frac{1}{p} \log A + o(1/p) \Big) = g(x_\ast) \Big( 1 – \frac{d}{2p} \log p + O(1/p) \Big).$$ A surprising fact is that the second-order term does not depend on anything but \(g(x_\ast)\) (beyond \(p\) and \(d\)). Note that this applies also to continuous log-sum-exp functions.
Applications in Bayesian inference
It turns out that Laplace’s motivation in deriving this general technique for approximating integrals was exactly Bayesian inference, which he in fact essentially re-discovered and extended (see an interesting account here). Let me now explain how Laplace’s method applies.
We consider a parameterized family of probability distributions with density \(p(x|\theta)\) with respect to some base measure \(\mu\) on \(x \in \mathcal{X}\), with \(\theta \in \Theta \subset \mathbb{R}^d\) a set of parameters.
As a running example (the one from Laplace in 1774), we consider the classical Bernoulli distribution for \(x \in \mathcal{X} = \{0,1\}\), and densities with respect to the counting measure, that is, the parameter \(\theta \in [0,1]\) is the probability that \(x=1\).
From frequentist to Bayesian inference. We are given \(n\) independent and identically distributed observations \(x_1,\dots,x_n \in \mathcal{X}\), from an unknown probability distribution \(q(x)\). One classical goal of statistical inference is to find the parameter \(\theta \in \Theta\) so that \(p(\cdot| \theta)\) is as close to \(q\) as possible.
In the frequentist framework, maximum likelihood estimation amounts to maximizing $$ \sum_{i=1}^n \log p(x_i | \theta)$$ with respect to \(\theta \in \Theta\). It comes with a series of guarantees, in particular (but not only) when \(q = p(\cdot | \theta)\) for a certain \(\theta \in \Theta\). For our running example, the maximum likelihood estimator \(\hat{\theta}_{\rm ML} = \frac{1}{n} \sum_{i=1}^n x_i\) is the frequency of non-zero outcomes.
In the Bayesian framework, the data are assumed to be generated by a certain \(\theta\), but now with \(\theta\) itself random with some prior probability density \(p(\theta)\) (with respect to the Lebesgue measure). Statistical inference typically does not lead to a point estimator (like the maximum likelihood estimator), but to the full posterior distribution of the parameter \(\theta\) given the observations \(x_1,\dots,x_n\).
The celebrated Bayes’ rule states that the posterior density \(p(\theta | x_1,\dots,x_n)\) can be written as: $$p(\theta | x_1,\dots,x_n) = \frac{ p(\theta) \prod_{i=1}^n p(x_i|\theta) }{p(x_1,\dots,x_n)},$$ where \(p(x_1,\dots,x_n)\) is the marginal density of the data (once the parameter has been marginalized out).
If pressured, a Bayesian will end up giving you a point estimate, but a true Bayesian will not give away the maximum a posteriori estimate (see here for some reasons why), but if you give him or her a loss function (e.g., the square loss), he or she will give away (reluctantly) the estimate that minimizes the posterior risk (e.g., the posterior mean for the square loss).
Bernoulli and Beta distributions. In our running Bernoulli example for coin tossing, it is standard to put a conjugate prior on \(\theta \in [0,1]\), which is here a Beta distribution with parameters \(\alpha\) and \(\beta\), that is, $$p(\theta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} \theta^{\alpha-1} ( 1- \theta)^{\beta-1}.$$ The posterior distribution is then also a Beta distribution with parameters \(\alpha + \sum_{i=1}^n x_i\) and \(\beta + \sum_{i=1}^n ( 1- x_i)\). The posterior mean is $$\mathbb{E} [ \theta | x_1,\dots,x_n ] = \frac{\alpha+ \sum_{i=1}^n x_i}{n + \alpha + \beta},$$ and corresponds to having pre-observed \(\alpha\) ones and \(\beta\) zeroes (this is sometimes referred to as Laplace smoothing). However, it is rarely possible to compute the posterior distribution in closed form, hence the need for approximations.
Laplace approximation. Thus, in Bayesian inference, integrals of the form $$ \int_{\Theta} h(\theta) p(\theta) \prod_{i=1}^n p(x_i|\theta) d\theta$$ for some function \(h: \Theta \to \mathbb{R}\), are needed. For example, computing the marginal likelihood corresponds to \(h=1\).
By taking logarithms, we can write $$\int_{\Theta} h(\theta) p(\theta) \prod_{i=1}^n p(x_i|\theta) d\theta = \int_{\Theta} h(\theta) \exp\Big( \log p(\theta) + \sum_{i=1}^n \log p(x_i|\theta) \Big) d\theta, $$ and with \(f_n(\theta) = \ – \frac{1}{n} \log p(\theta) \ – \frac{1}{n} \sum_{i=1}^n \log p(x_i|\theta),\) we have an integral in Laplace form, that is, $$\int_{\Theta} h(\theta) \exp( -n f_n(\theta))d\theta,$$ with a function \(f_n\) that now varies with \(n\). This simple variation does not matter as because of the law of large numbers, when \(n\) is large, \(f_n(\theta)\) tends to a fixed function \(\mathbb{E} \big[ \log p(x|\theta) \big]\).
The Laplace approximation thus requires to compute the minimizer of \(f_n(\theta)\), which is exactly the maximum a posteriori estimate \(\hat{\theta}_{\rm MAP}\), and use the approximation: $$ \int_{\Theta} h(\theta) \exp( -n f_n(\theta))d\theta \approx (2\pi / n)^{d/2} \frac{h( \hat{\theta}_{\rm MAP})}{(\det f_n^{\prime \prime}( \hat{\theta}_{\rm MAP}))^{1/2}} \exp( – n f_n( \hat{\theta}_{\rm MAP})).$$
Gaussian posterior approximation. Note that the Laplace approximation exactly corresponds to approximating the log-posterior density by a quadratic form and thus approximating the posterior by a Gaussian distribution with mean \(\hat{\theta}_{\rm MAP}\) and covariance matrix \(\frac{1}{n} f_n^{\prime \prime}( \hat{\theta}_{\rm MAP})^{-1}\). Note that Laplace’s method gives one natural example of such Gaussian approximation and that variational inference can be used to find better ones.
Example. We consider the Laplace approximation of a Beta random variable, that is a Gaussian with mean at the mode of the original density and variance equal to the inverse of the second derivative of the log-density. Below, the mean \(\alpha / (\alpha +\beta)\) is set to a constant, while the variance shrinks due to an increasing \(\alpha+\beta\) (which corresponds to the number of observations in the Bayesian interpretation above).
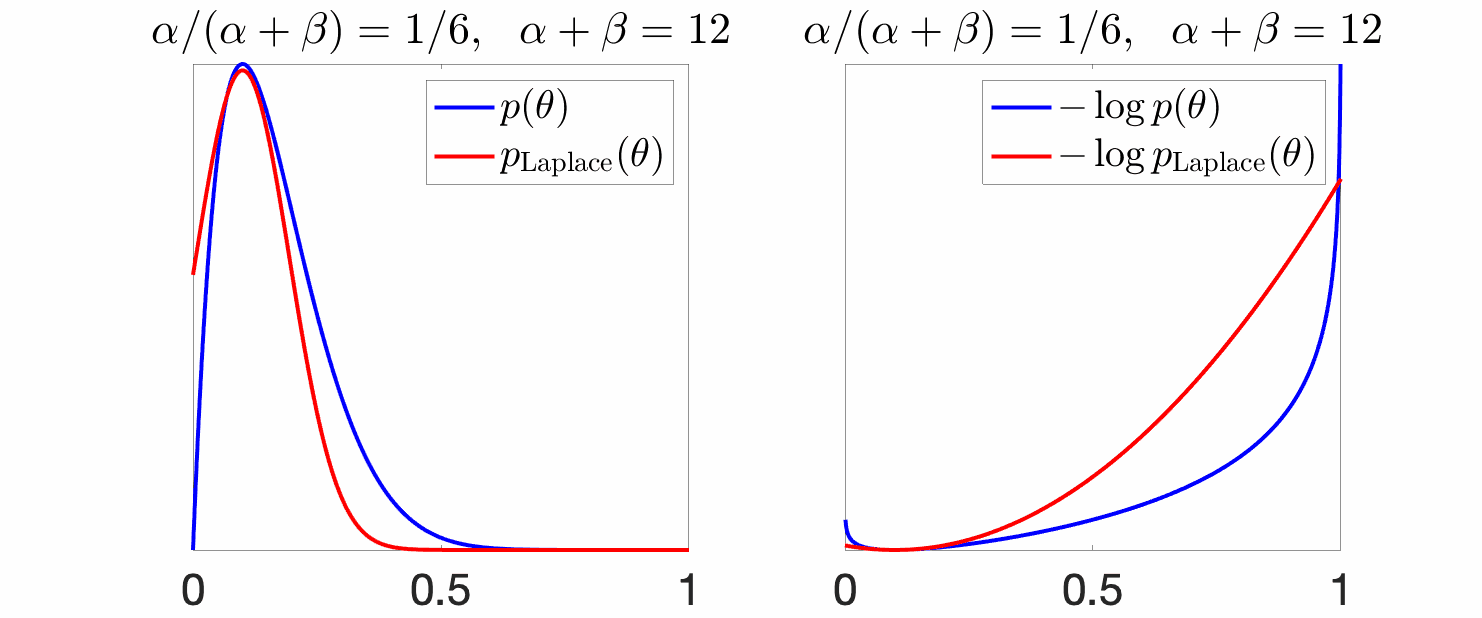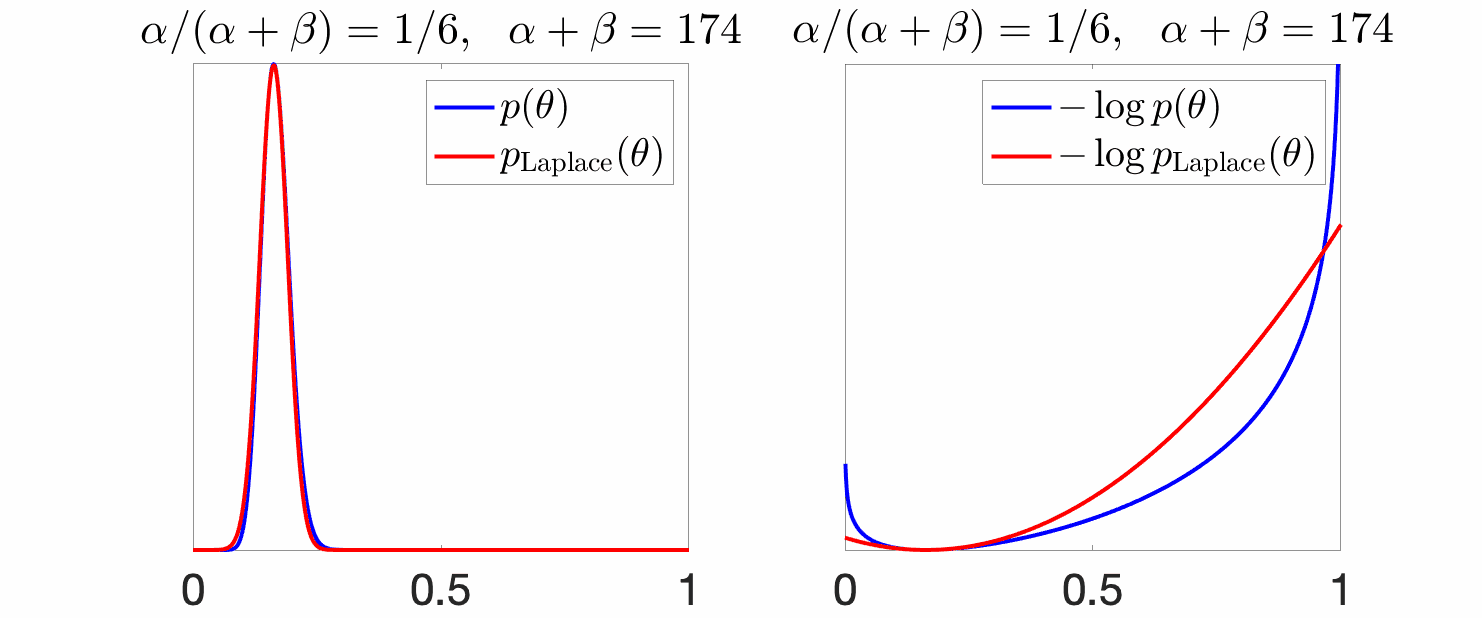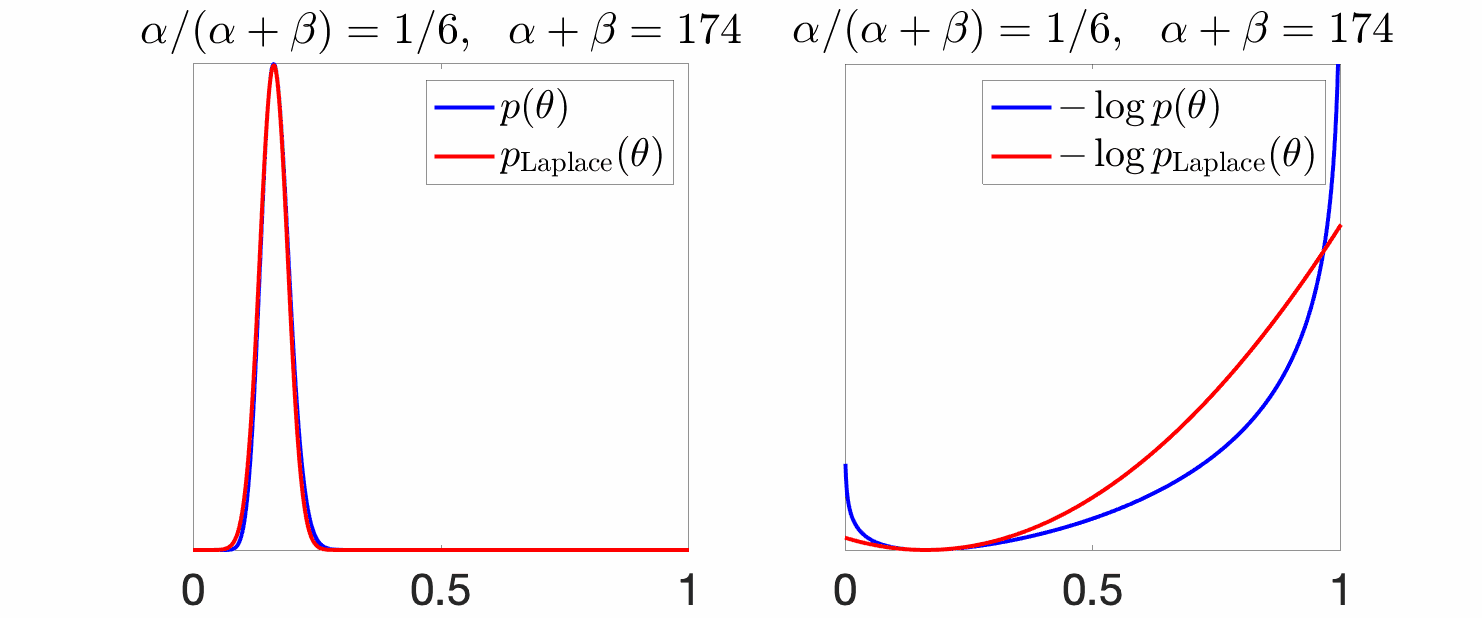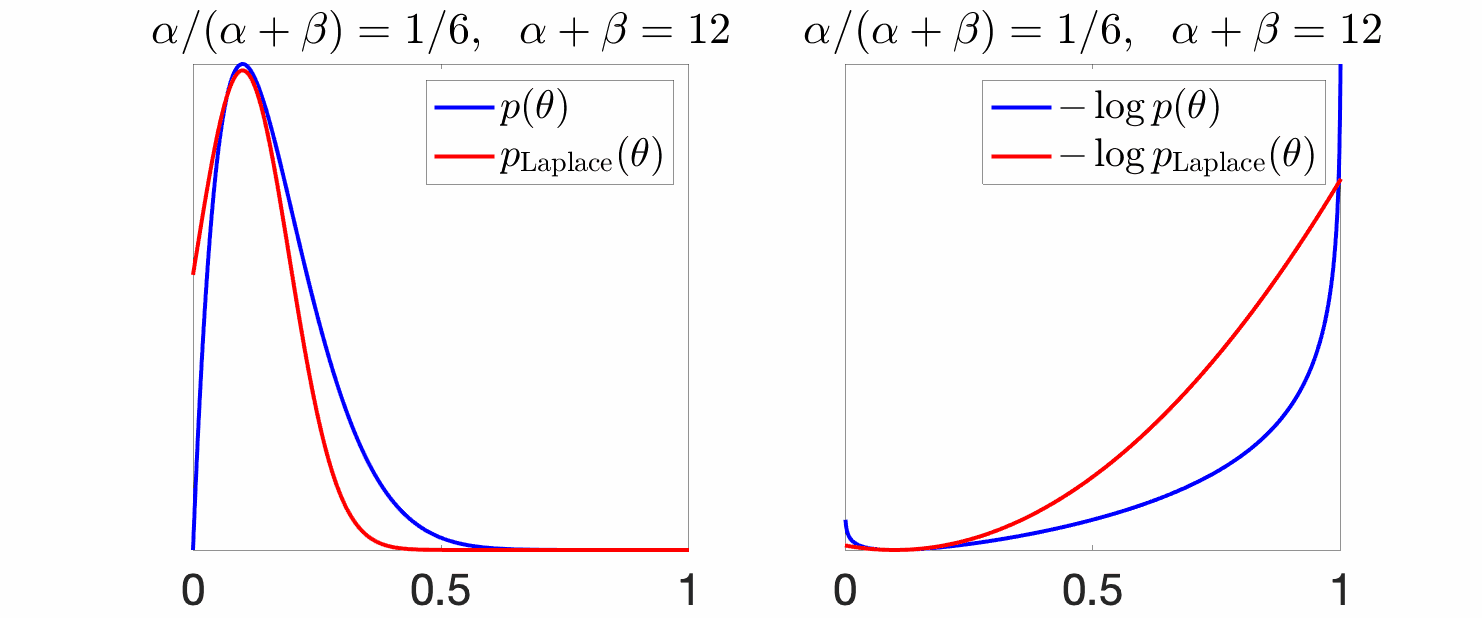
We see above, that for large variances (small \(\alpha +\beta\)), the Gaussian approximation is not tight, while it becomes tighter as the mass gets concentrated around the mode.
Extensions
High-order expansion. The approximation is based on Taylor expansions of the functions \(h\) (order \(0\)) and \(f\) (order \(2\)). In order to obtain extra terms of the form \(t^{d/2+\nu}\), for \(\nu\) a positive integer, we need higher-order derivatives of \(h\) and \(f\). In more than one dimension, that quickly gets complicated (see, e.g., [3, 4]).
One particular case which is interesting in one dimension is \(h(x) \sim A ( x- x_\ast)^\alpha\), and \(f(x)-f(x_\ast) = B|x-x_\ast|^{\beta}\). Note that \(\alpha=0\) and \(\beta=2\) corresponds to the regular case. A short calculation gives the equivalent \(I(t) \sim \frac{2}{2+\beta} \frac{A \Gamma\big( \frac{\alpha+1}{\beta} \big)}{(tB)^{\frac{\alpha+1}{\beta}}}\).
Stationary phase approximation. We can also consider integrals of the form $$I(t) = \int_K h(x) \exp( – i t f(x) ) dx,$$ where \(i\) is the usual square root of \(-1\). Here, the main contribution also comes from vectors \(x\) where the gradient of \(f\) is zero. This can be further extended to more general complex integrals.
When Napoléon meets Laplace and Lagrange
As a conclusion, I cannot resist mentioning a classical (potentially not totally authentic) anecdote about encounters between Laplace and Lagrange, two mathematical heroes of mine, and Napoléon, as described in [5, page 343]:
Laplace went in state to beg Napoleon to accept a copy of his work, and the following account of the interview is well authenticated, and so characteristic of all the parties concerned that I quote it in full. Someone had told Napoleon that the book contained no mention of the name of God; Napoleon, who was fond of putting embarrassing questions, received it with the remark, “M. Laplace, they tell me you have written this large book on the system of the universe, and have never even mentioned its Creator.” Laplace, who, though the most supple of politicians, was as stiff as a martyr on every point of his philosophy, drew himself up and answered bluntly, “Je n’avais pas besoin de cette hypothèse-là.” Napoleon, greatly amused, told this reply to Lagrange, who exclaimed, “Ah! c’est une belle hypothèse; ça explique beaucoup de choses.”
W. W. Rouse Ball, A Short Account of the History of Mathematics, 1888.
References
[1] Pierre-Simon Laplace. Mémoire sur la probabilité des causes par les événements, Mémoires de l’Académie royale des sciences de Paris (Savants étrangers), t. VI. p. 621, 27-65, 1774.
[2] Norman Bleistein, Richard A. Handelsman. Asymptotic Expansions of Integrals. Dover
Publications, 1986.[3] Stephen M. Stigler. Laplace’s 1774 memoir on inverse probability. Statistical Science, 1(3):359-378, 1986.
[3] Luke Tierney, Robert E. Kass, Joseph B. Kadane. Fully exponential Laplace approximations to expectations and variances of nonpositive functions. Journal of the American Statistical Association, 84(407): 710-716, 1989.
[4] Zhenming Shun, Peter McCullagh. Laplace approximation of high dimensional integrals. Journal of the Royal Statistical Society: Series B (Methodological) 57(4): 749-760, 1995.
[5] W. W. Rouse Ball. A Short Account of the History of Mathematics, 1888.
great post !
any chance this result can be extended in the case where f and h are matrix functions ?
Most probably, if you can use the same argument that the integral is dominated by contributions around a single point.
Francis
Hello Francis,
For the example with Stirling number, K = [0, +\infty] is not compact. How can we apply the result of Laplace?
Good point. I would say it applies in the same way by cutting the integral in pieces.
Francis