Unraveling spectral properties of kernel matrices – I

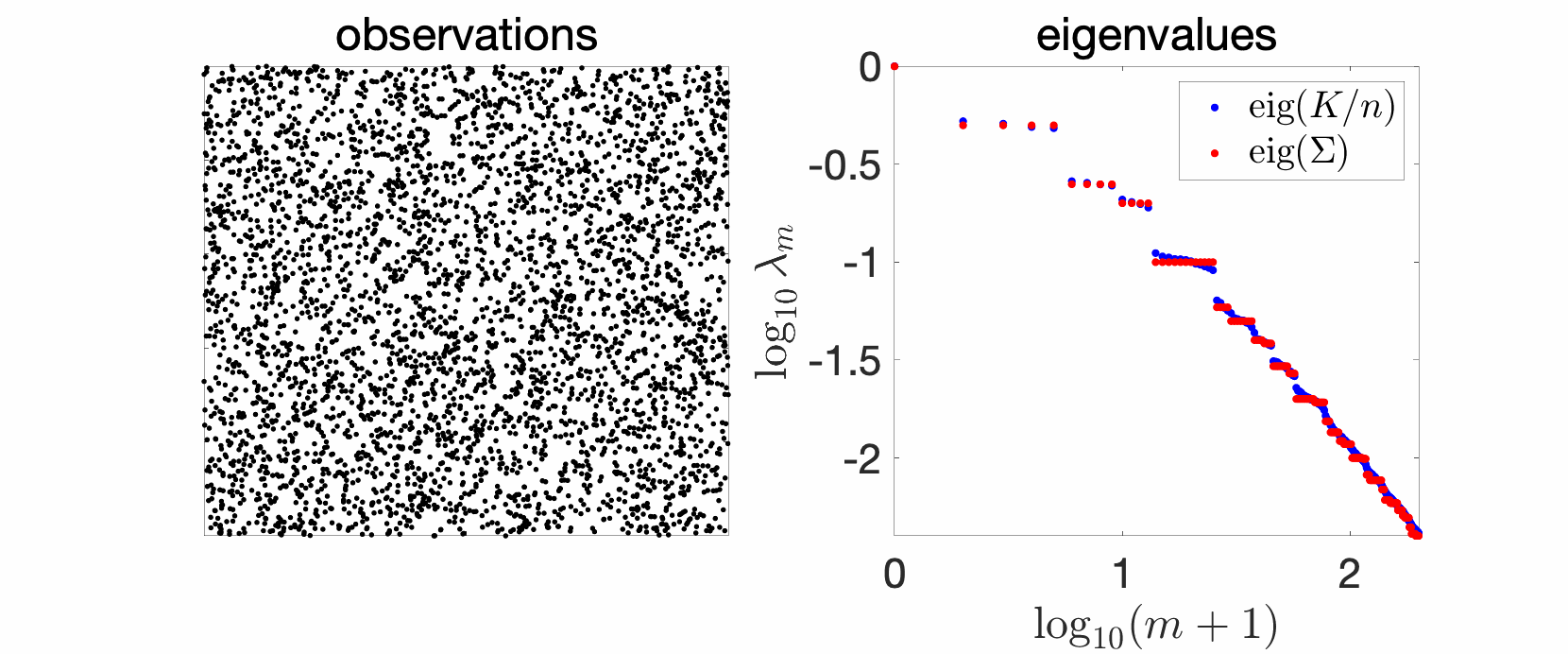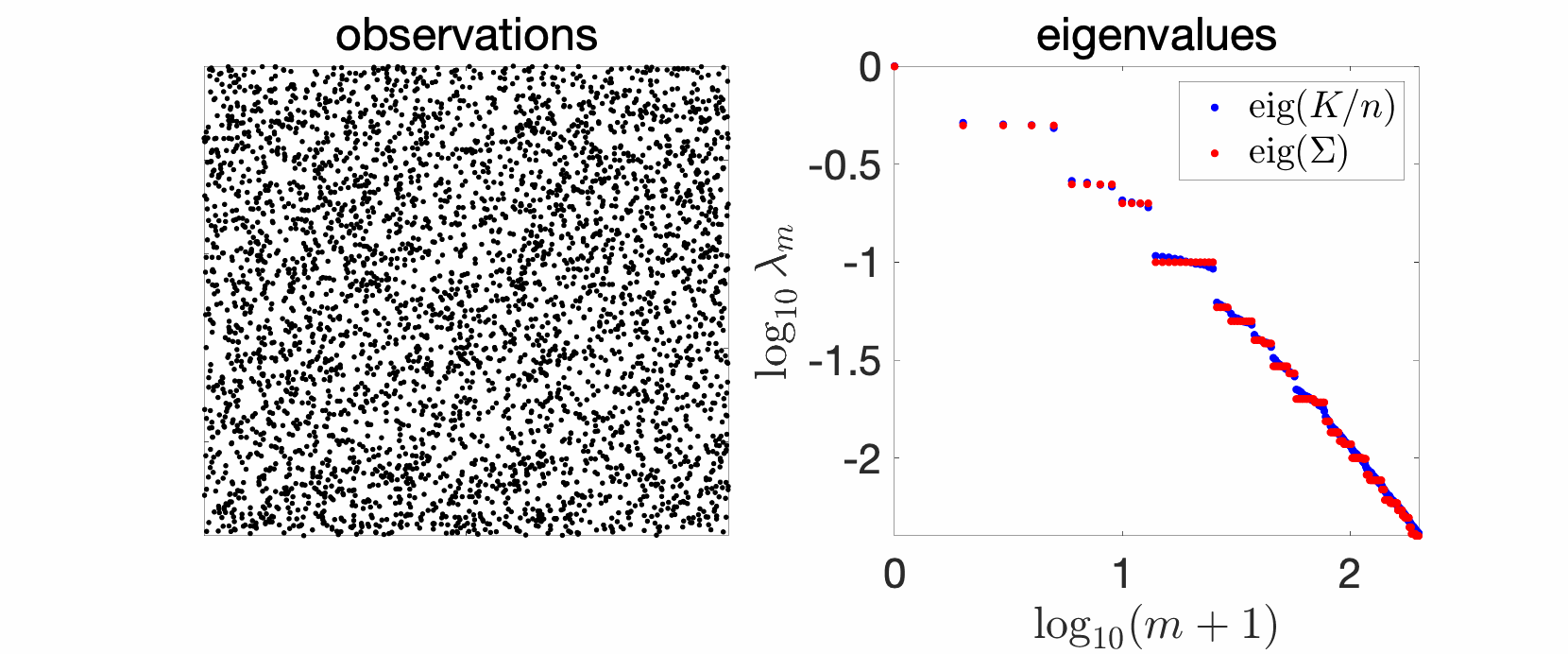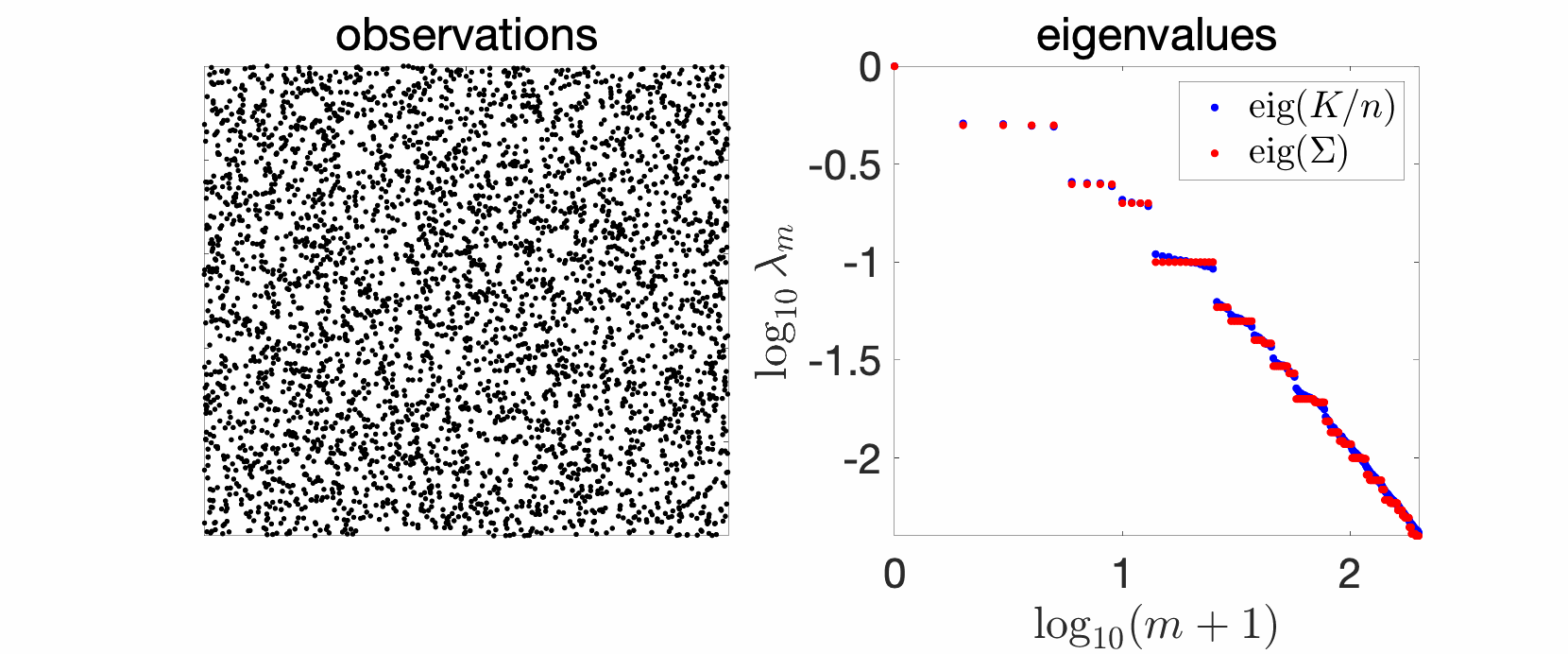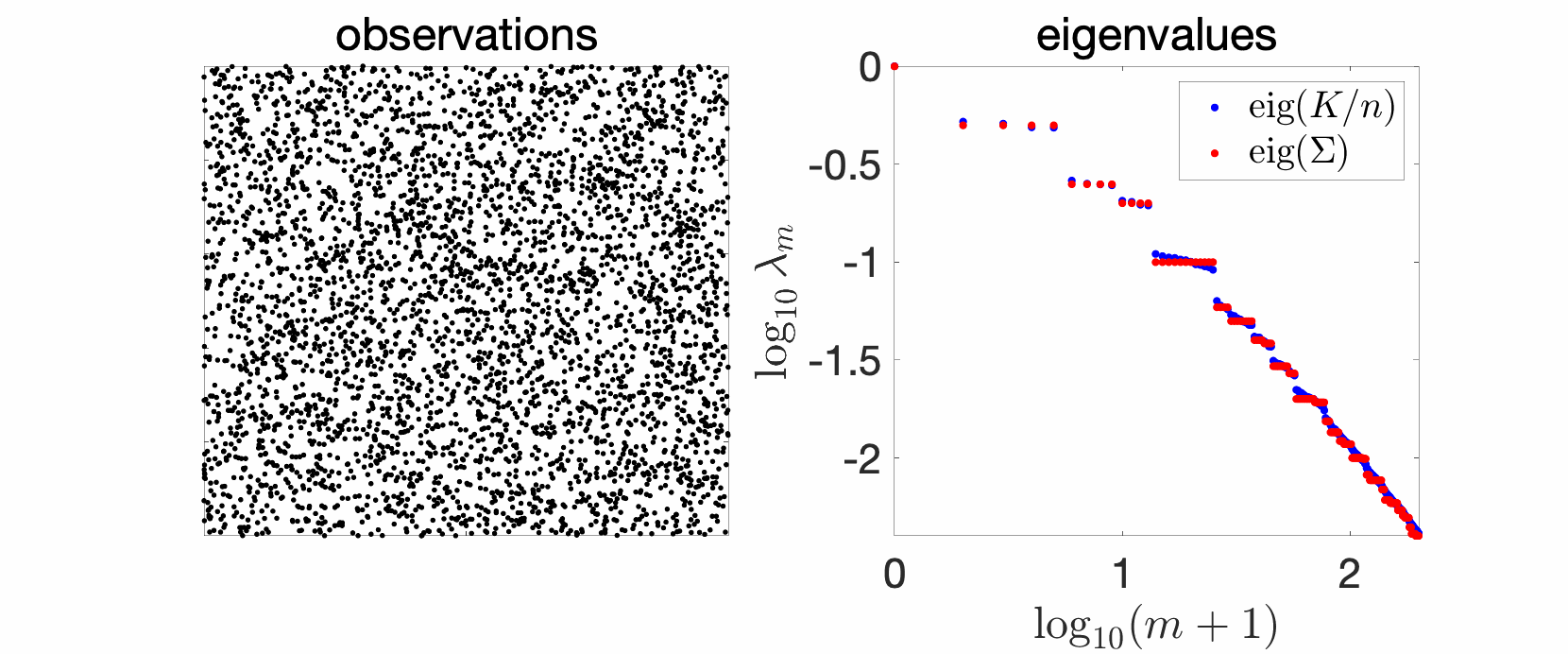
Since my early PhD years, I have plotted and studied eigenvalues of kernel matrices. In the simplest setting, take independent and identically distributed (i.i.d.) data, such as in the cube below in 2 dimensions, take your favorite kernels, such as the Gaussian or Abel kernels, plot eigenvalues in decreasing order, and see what happens. The goal of this sequence of blog posts is to explain what we observe.

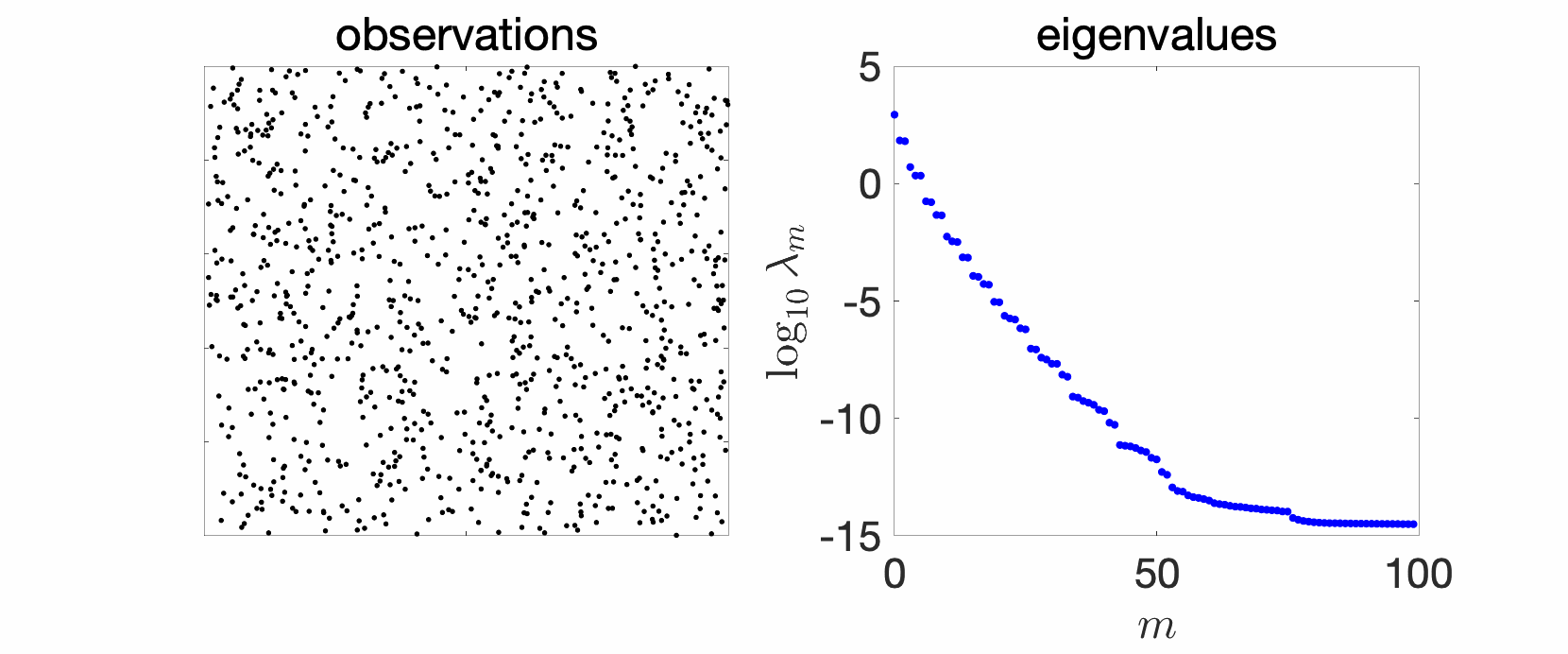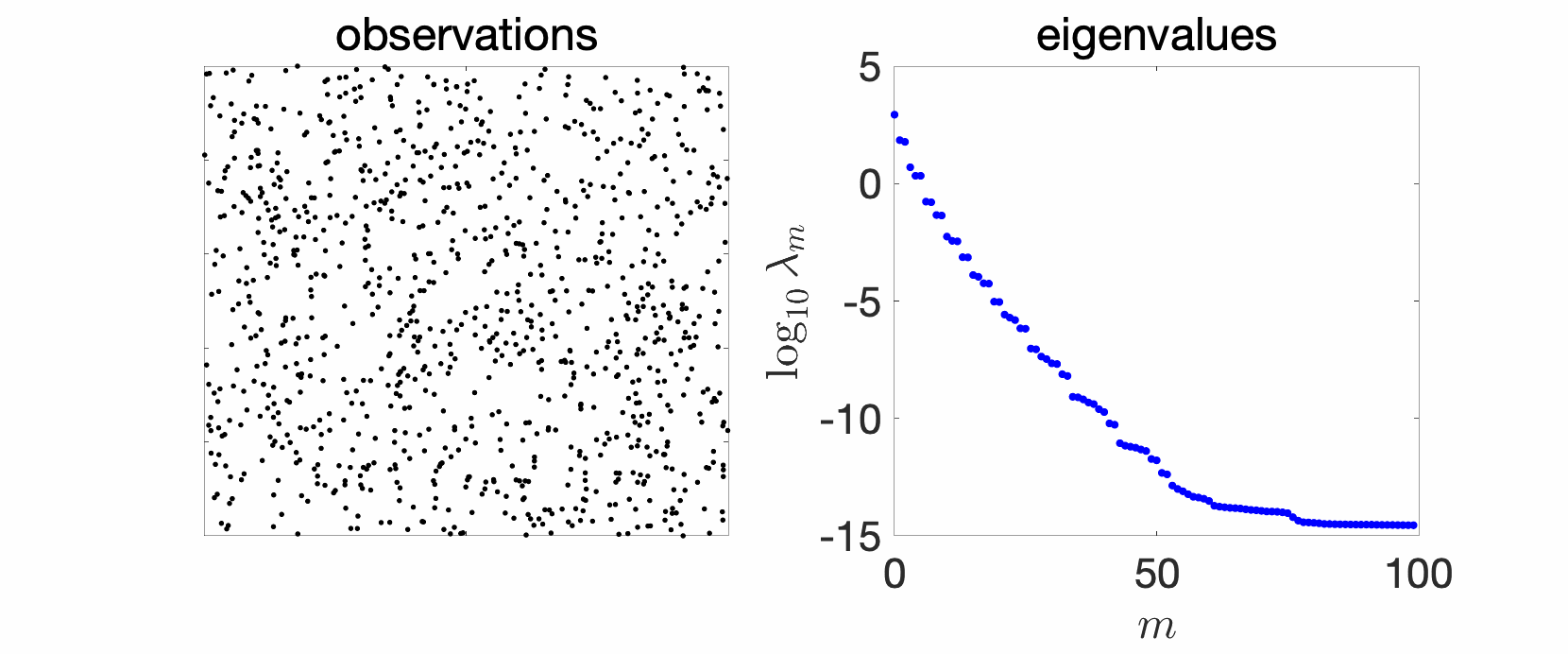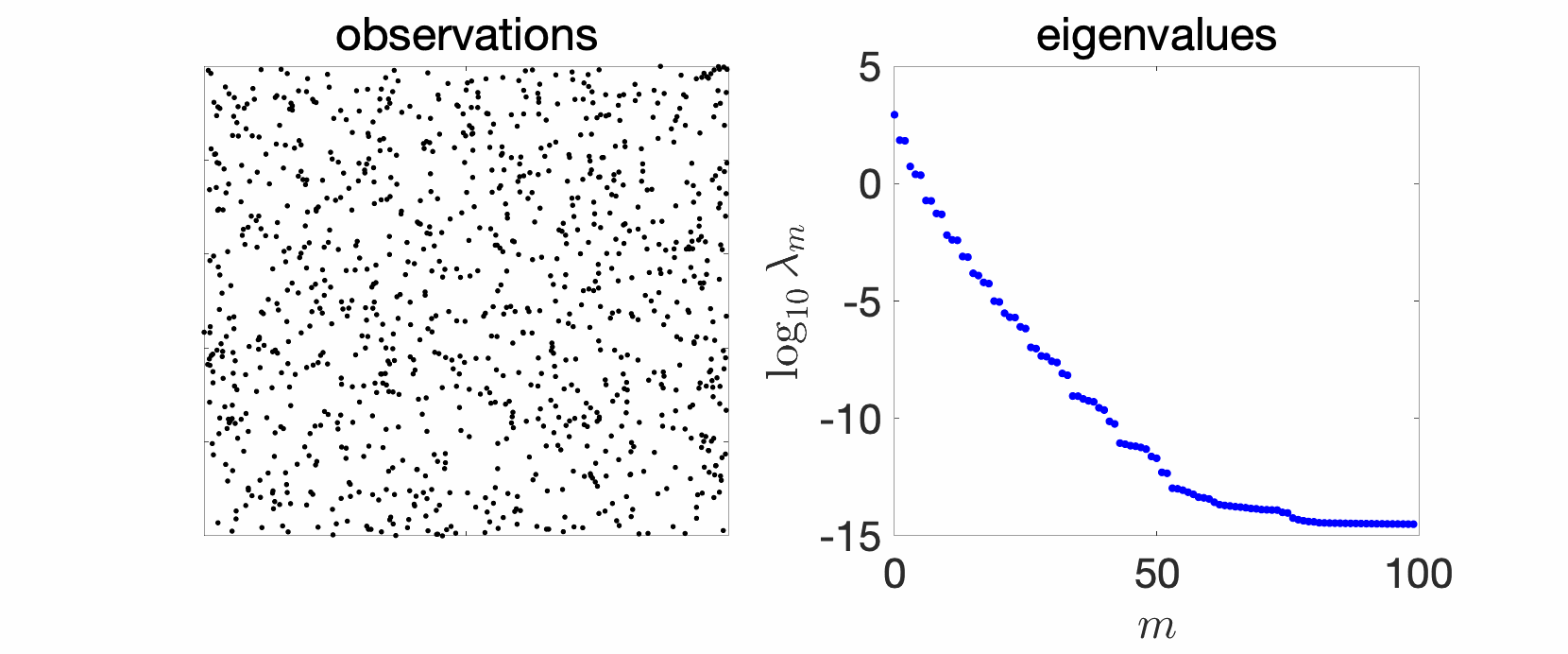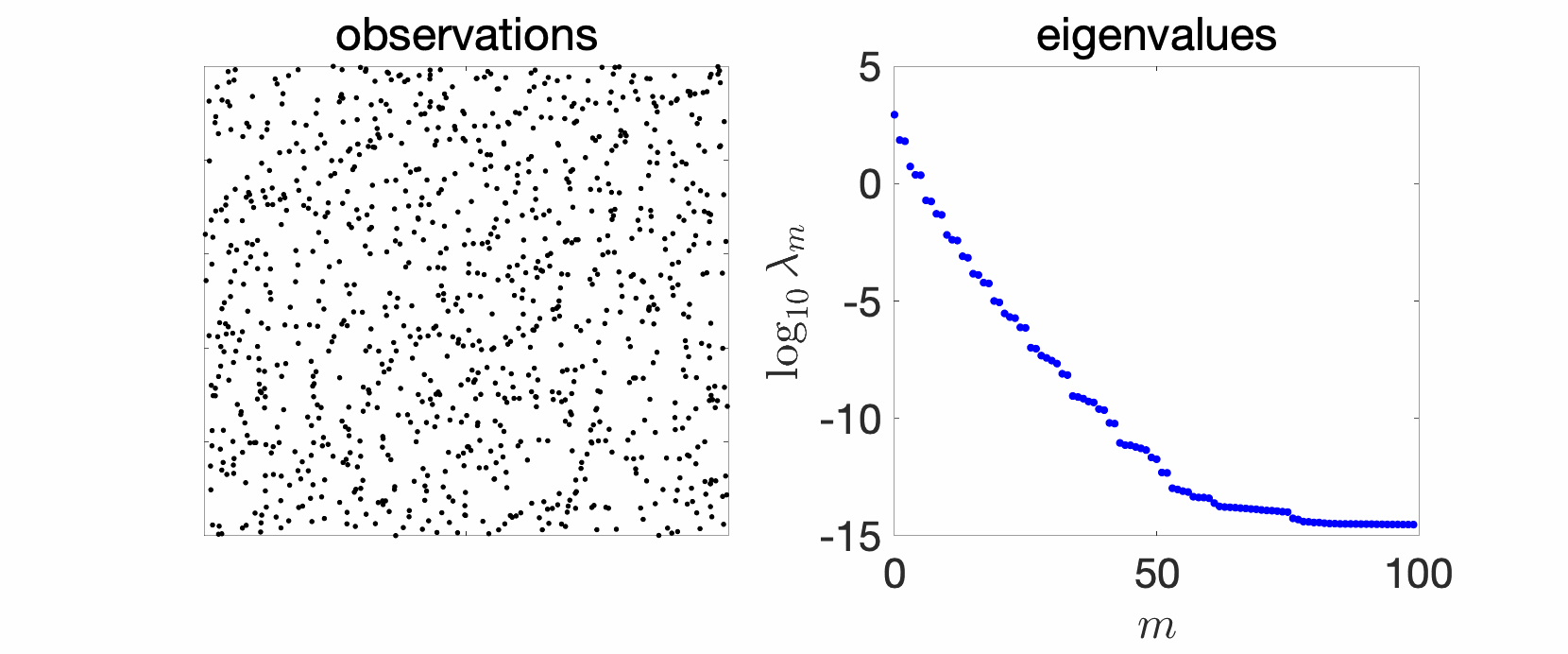
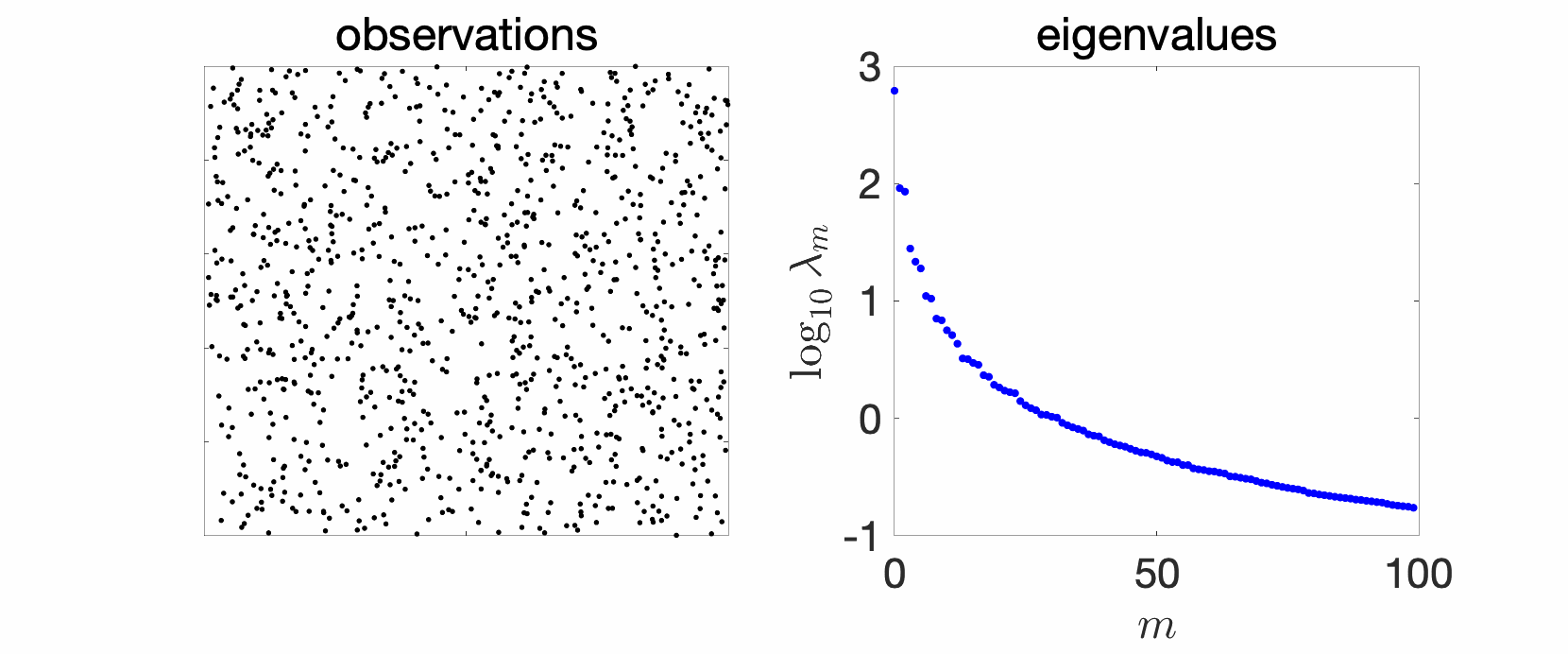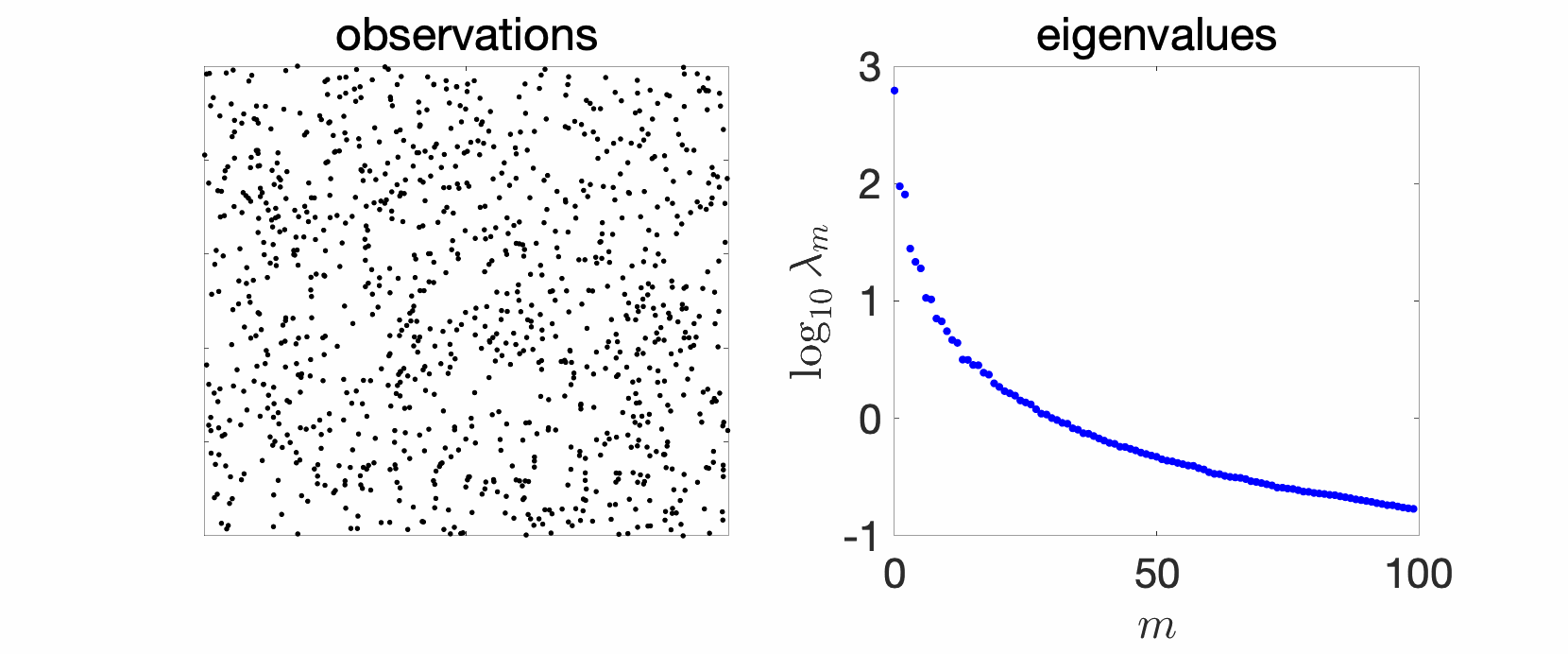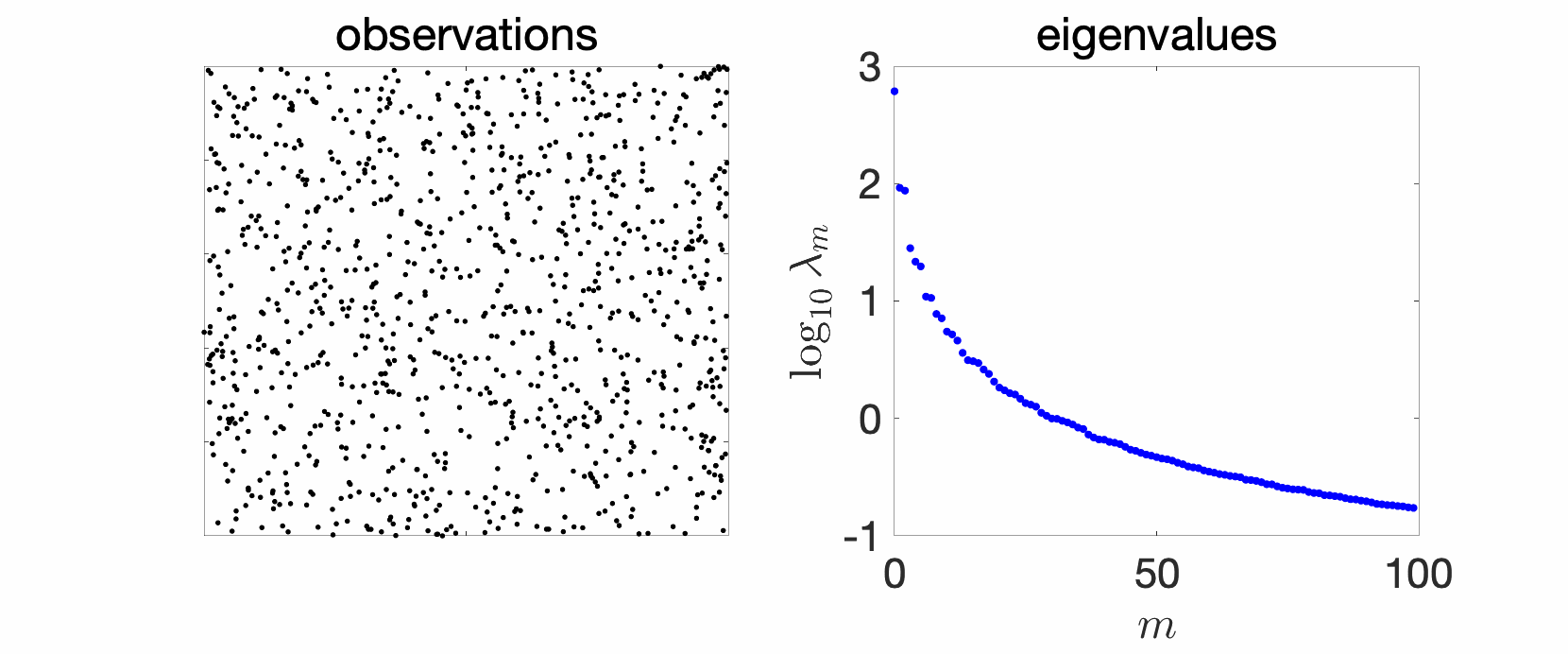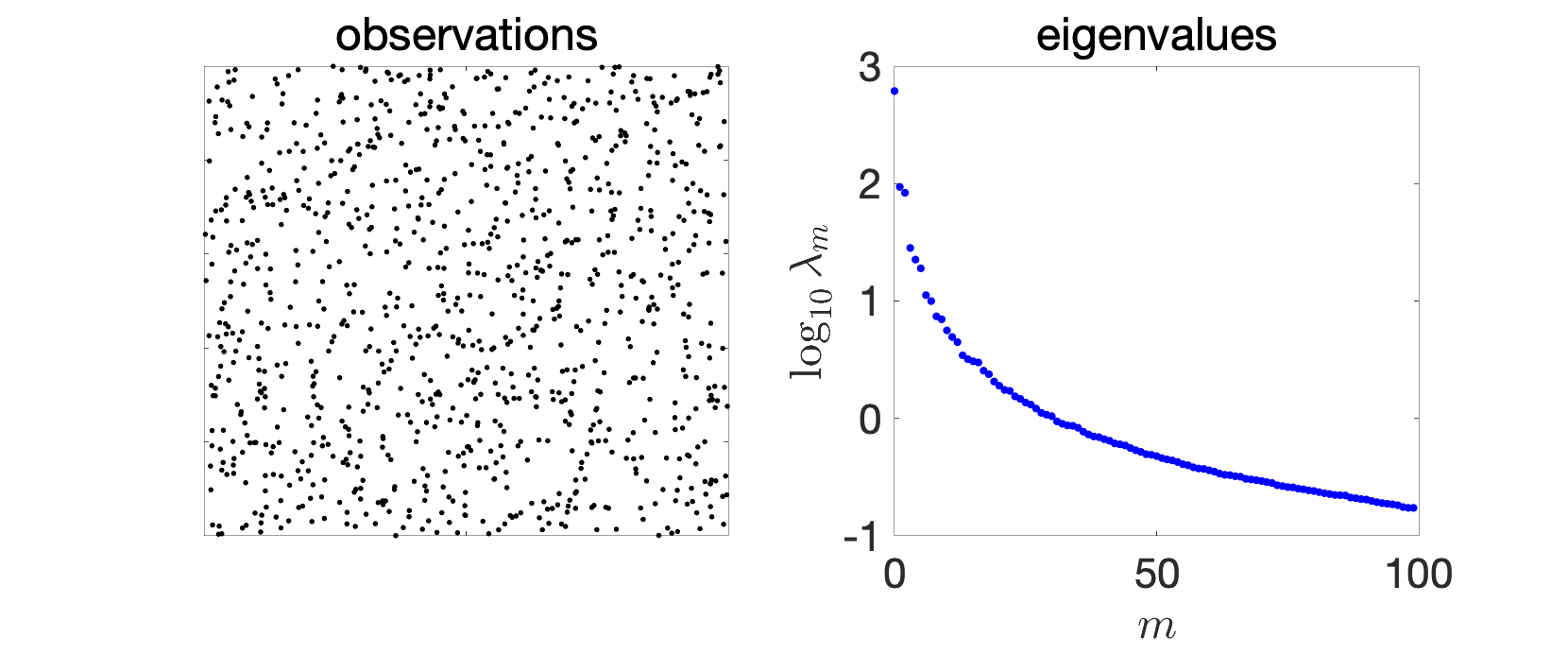
In the plots above we see a certain number of things:

• Over replications, we see a certain stability, that is, eigenvalues do not change much. We will see that this is due to a well-defined limit when the number \(n\) of observations tend to infinity, and will precisely study the limit behavior.
• Largest eigenvalues seem to appear with levels, (not surprisingly) reminiscent of energy levels in physics. This can also be explained, by the tensorial nature of the problem and symmetries.
• The two kernels have a different set of eigenvalues, with fast decay for the Gaussian kernel (machine precision is already attained at the \(100\)-th eigenvalue), and slower for the Abel kernel. The spectral behavior can also be well explained based on Fourier analysis.

Why is this important?

Eigenvalue decays of kernel matrices come up in most statistical and algorithmic analyses associated with kernel methods, or where kernel methods are used to explain the statistical behavior of other learning frameworks such as neural networks (see, e.g., [1, Chapter 9]). Here are a few instances.

Control of approximation properties of kernel matrices by column sampling. A kernel matrix \(K \in \mathbb{R}^{n \times n}\) is a large object whose algorithmic manipulation can lead to running-time complexities that are at least \(O(n^2)\) just to compute the matrix, and often more, e.g., \(O(n^3)\) to implement learning algorithms. This is a common reason to discard kernel methods when \(n\) is large. However, there exist several methods to even avoid computing the full kernel matrix, and obtain running-time complexities that are sub-quadratic in \(n\), and sometimes slightly super-linear in \(n\).

A classical technique from numerical linear algebra is to approximate a positive semidefinite matrix \(K\) from a subset of its columns, which come under many different names, e.g., Nyström method [2], incomplete Cholesky decomposition [3, 4] or CUR matrix decompositions [5]. Another classical technique is to use random features [6]. There is now a significant body of literature characterizing the required rank of these approximations [5, 7, 8, 9, 10]. All of them highlight that the spectral decay of the kernel matrices, that is, how fast eigenvalues go to zero, is key.

Convergence rates of optimization algorithms. Many supervised learning formulations based on optimization and kernel methods often end up having the kernel matrix as the Hessian of the problem. Thus, its condition number (ratio of largest to smallest eigenvalue) characterizes the convergence of gradient-based techniques, hence the need for a precise spectral analysis. Note that the convergence of (stochastic) optimization algorithms depend on much more than the condition number and, in the infinite-dimensional kernel context, how fast eigenvalues decay to zero is crucial, both for theoretical analysis (see, e.g., [11]) and for the design of potential acceleration schemes (see, e.g., [12, 13]).

Generalization guarantees for kernel methods. The spectral decay characterizes the amount of correlation between features. Not surprisingly, it is crucial in the fine analysis of kernel methods, as detailed below once covariance operators are introduced.

Asymptotic analyses

In this sequence of blog posts, we thus consider observations \(x_1,\dots,x_n\) in a set \(\mathcal{X}\) (which can be quite arbitrary) sampled independently and identically distributed (i.i.d.) from a probability distribution \(\mu\), and a positive definite kernel \(k: \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). We then form the kernel matrix \(K \in \mathbb{R}^{n \times n}\), defined as: $$K_{ij} = k(x_i,x_j).$$ It is a random positive semi-definite matrix, thus with \(n\) real eigenvalues.

Several analyses have been carried out to understand the spectrum of \(K\). When \(\mathcal{X}=\mathbb{R}^d\) and the distribution of inputs has sufificient symmetries or independence properties, random matrix theory can be used to study the spectrum as both \(d\) (the dimension of the input space \(\mathcal{X}\)) and \(n\) (number of observations) grow [14]. In another more recent line of work, asymptotic analyses around the “flat” limit (constant kernel matrices) can be carried out without the need to let \(n\) tend to infinity (see [15] and references therein). In this blog post, I will describe an analysis that is classical in statistics, optimization and machine learning, that is, the limit when \(n\) tends to infinity (with the input space \(\mathcal{X}\) being fixed). We will show below that the eigenvalues will be related to the eigenvalues of the potentially infinite-dimensional covariance operator which we now define.

Covariance operator

We define \(\Sigma\) the (non-centered) covariance operator associated with the probability measure \(\mu\) and the kernel \(k\) as follows. Like all positive definite kernels, we can write it as (a key result due to Aronszajn in 1950): $$k(x,y) = \langle \varphi(x) , \varphi(y) \rangle$$ for any feature map \(\varphi: \mathcal{X} \to \mathcal{H}\) that represents the positive definite kernel, with \(\mathcal{H}\) a Hilbert space, with norm \(\| \cdot \|\) and dot product \(\langle \cdot, \cdot \rangle\).

We assume that \(\int_\mathcal{X} k(x,x) d\mu(x)\) is finite, which is a weak assumption as for many kernel functions, \(k(x,x)\) is uniformly bounded. The covariance operator is then defined from \(\mathcal{H}\) to \(\mathcal{H}\) through $$\langle f, \Sigma g \rangle = \int_{\mathcal{X}} \langle f,\varphi(x) \rangle \langle g,\varphi(x) \rangle d\mu(x),$$ which corresponds to the notation \(\displaystyle\Sigma = \int_{\mathcal{X}} \varphi(x) \otimes \varphi(x) d\mu(x).\) In finite dimension, we can identify it to the matrix \(\displaystyle \int_{\mathcal{X}} \varphi(x) \varphi(x)^\top d\mu(x)\). Throughout this blog post, we assume that \(\mathcal{H}\) is infinite-dimensional.

In technical terms, the operator \(\Sigma\) is compact. Thus, there exists a non-increasing sequence of strictly positive eigenvalues \((\lambda_m)_{m \geqslant 0}\) tending to zero, and of eigenvectors (elements of \(\mathcal{H}\) that form an orthonormal basis) \((f_m)_{m \geqslant 0}\) such that \(\Sigma f_m = \lambda_m f_m\), that is, $$\Sigma f_m = \int_{\mathcal{X}} \varphi(x) \langle \varphi(x), f_m \rangle d\mu(x) = \lambda_m f_m, \tag{1}$$ which we can write for any \(y \in \mathcal{X}\), $$\langle \varphi(y), \Sigma f_m \rangle = \int_{\mathcal{X}} k(x,y) \langle \varphi(x), f_m \rangle d\mu(x) = \lambda_m \langle \varphi(y), f_m\rangle .$$

Thus, the functions \(g_m: x \mapsto \langle \lambda_m^{-1/2} \varphi(x), f_m \rangle\) are eigenfunctions (e.g., eigenvectors) of the integral operator from \(L_2(\mu)\) to \(L_2(\mu)\) defined as $$T g(x) = \int_{\mathcal{X}} k(x,y) g(y)d\mu(y).$$ The factor \(\lambda_m^{-1/2}\) is here to ensure that \(\int_{\mathcal{X}} g_m(x)^2 d\mu(x) = 1\), as a consequence of Eq. \((1)\), that is, the functions \(g_m\) have unit norm in \(L_2(\mu)\).

We can then decompose in the orthonormal basis of \(\mathcal{H}\) the vector \(\varphi(y) = \sum_{m \geqslant 0} \langle \varphi(y), f_m \rangle f_m\), leading to by taking the dot-product with \(\varphi(x)\): $$k(x,y) = \sum_{m \geqslant 0} \lambda_m \langle \varphi(y), \lambda_m^{-1/2} f_m \rangle \langle \varphi(x), \lambda_m^{-1/2} f_m \rangle= \sum_{m \geqslant 0} \lambda_m g_m(x) g_m(y),$$ which is a Mercer decomposition.

Ridge regression. Following [16], we can consider regression problems where outputs \(y\) are modeled as \(y=f(x) + \varepsilon\), where \(f\) is an arbitrary function and \(\varepsilon\) a random variable with zero mean and variance \(\sigma^2\). If kernel ridge regression (least-squares empirical loss for the prediction function \(f:x \mapsto \langle \varphi(x), \theta \rangle\) with Hilbertian regularizer \(\lambda \| \theta \|^2\)) is used, then the expected prediction performance depends on the noise variance with a term of the form $$ \sigma^2 \sum_{m \geqslant 0} \frac{\lambda_m}{\lambda_m + \lambda}= \sigma^2{\rm tr} \big[ \Sigma (\Sigma + \lambda I)^{-1} \big],$$ where \((\lambda_m)_{m \geqslant 0}\) are the eigenvalues of the covariance operator defined above, and \(\lambda\) is the regularization parameter. The term \({\rm tr} [ \Sigma (\Sigma + \lambda I)^{-1} ]\) is usually referred to as the degrees of freedom, and thus key to understanding the sampling behavior of methods based on kernels.

Degrees of freedom and boundedness of eigenfunctions. Since the function \(\mu \mapsto \mu / (\mu+\lambda)\) is increasing on \(\mathbb{R}_+\), from \(0\) to \(1\), with value \(1/2\) at \(\mu=\lambda\), the degrees of freedom can be seen as a “soft count” of the number of eigenvalues that are greater than \(\lambda\). Since we have assumed that we have an infinite non-increasing sequence of eigenvalues that tend to zero, \({\rm tr} [ \Sigma (\Sigma + \lambda I)^{-1} ]\) tends to infinity when \(\lambda\) tends to zero, and the rate at which it tends to infinity is essentially equivalent to the rate at which \(\lambda_m\) tends to zero when \(m\) tends to infinity. For example, when \(\lambda_m \sim m^{-\alpha}\) (up to constants) for \(\alpha > 1\), then \({\rm tr} [ \Sigma (\Sigma + \lambda I)^{-1} ] \sim \lambda^{-1/\alpha}\) (up to constants), and for \(\lambda_m \sim \rho^m\), then we get a dependence in \(\frac{1}{\rho} \log \frac{1}{\lambda}\)(see, e.g., [7, Appendix C], for detailed computations).

In the analysis of kernel methods, another notion of degrees of freedom is often used (like done in probabilistic statements below), which is sometimes referred to as the maximal degrees of freedom, or maximal leverage scores, that we define as $${\rm df}(\lambda) = \sup_{x \in \mathcal{X}}\ \langle \varphi(x), (\Sigma + \lambda I)^{-1} \varphi(x) \rangle.$$ We always have \({\rm tr} [ \Sigma (\Sigma + \lambda I)^{-1} ] \leqslant {\rm df}(\lambda)\), and if the eigenfunctions \(g_m\) are uniformly bounded in \(L_\infty\)-norm, we have $$ {\rm df}(\lambda) \leqslant \sup_{x \in \mathcal{X}} \sup_{m \geqslant 0} | g_m(x)|^2 \cdot {\rm tr} [ \Sigma (\Sigma + \lambda I)^{-1} ],$$ and thus \({\rm df}(\lambda)\) and \({\rm tr} [ \Sigma (\Sigma + \lambda I)^{-1} ]\) have the same growth.

Removing randomness

We can now explain the behavior of eigenvalues of \(\frac{1}{n} K\) when \(\mu\) is a probability measure, by noticing that its \(n\) eigenvalues are the first \(n\) eigenvalues of the empirical covariance operator (also from \(\mathcal{H}\) to \(\mathcal{H}\)) $$\hat{\Sigma} = \frac{1}{n} \sum_{i=1}^n \varphi(x_i) \otimes \varphi(x_i) $$ (this is a consequence of the non-zero eigenvalues of \(\frac{1}{n} \Phi \Phi^\ast\) being exactly the ones of \(\frac{1}{n} \Phi^\ast \Phi\) for any matrix or linear operator \(\Phi\)).

We can then rely on the fact that \(\hat{\Sigma}\) tends to \(\Sigma\) in a variety of potential norms and probabilistic statements. The simplest is convergence in Hilbert-Schmidt norm (which is the Frobenius norm in finite dimension), that is, $$\mathbb{E} \big[ \| \Sigma \, – \hat{\Sigma} \|_{\rm HS}^2 \big] = \frac{1}{n} \mathbb{E} \big[ \| \Sigma \, – \varphi(x) \otimes \varphi(x) \|_{\rm HS}^2\big] \leqslant \frac{1}{n}\int_\mathcal{X} k(x,x)^2 d\mu(x).$$ Note here that the fact that our features \(\varphi\) are infinite-dimensional never appeared, as long as the integral above is finite, which is the case as soon as the kernel is bounded on \(\mathcal{X} \times \mathcal{X}\).

By the Hoffman-Wielandt inequality [17], we get $$ \sum_{m \geqslant 0} | \lambda_m(\Sigma) \, – \lambda_m(\hat{\Sigma}) |^2 \leqslant \| \Sigma \, – \hat{\Sigma} \|_{\rm HS}^2,$$ and thus all eigenvalues converge at least at rate \(O(1/\sqrt{n})\). This can be extended to other norms, in particular through the use of the operator norm (largest eigenvalue in absolute value), with then a need for a careful treatment of infinite dimensions (see [18, 19] and the end of the post for an example).

However, given that eigenvalues \(\lambda_m\) converge to zero when \(m\) tends to infinity, and sometimes quite fast (as we explain below), a uniform approximation rate independent of \(m\) does not correspond to what we see in the figure above, where, in log-scale, we obtain variations that have a similar range for all \(m\). There exists more refined statements that are sharper, starting from [20], which shows that in the most regular situations (e.g., uniformly bounded eigenfunctions \(g_m\)), we obtain the bound up to logarithmic terms $$| \lambda_m(\Sigma) \, – \lambda_m(\hat\Sigma) | = O \Big( \lambda_m(\Sigma) \frac{r} {\sqrt{n}} + \sum_{i > r} \lambda_i(\Sigma) \Big),$$ which can be optimized with respect to \(r \in \{1,\dot,n\}\). It corresponds with the notations of this blog to $$| \lambda_m(\Sigma)\, – \lambda_m(\hat\Sigma) | = O \Big( \frac{{\rm df}(\lambda) } {\sqrt{n}} \lambda_m(\Sigma)+ \lambda {\rm df}(\lambda) \Big),$$ with a parameter \(\lambda >0\), that can be optimized. At the end of the post, by simply using a similar inequality as the Hoffman-Wielandt inequality, but this time on the matrix logarithm, we obtain a novel improved bound (still up to logarithmic terms) $$| \lambda_m(\Sigma) \, – \lambda_m(\hat\Sigma) | =O\Big( (\lambda_m(\Sigma) +\lambda) \cdot \sqrt{ \frac{{\rm df}(\lambda)}{n}}\Big).$$ See more details and comparisons at the end of this blog, and a detailed asymptotic analysis in [21].

(added January 9, 2024 : My colleague Alessandro Rudi pointed out that he already obtained the same result with a more direct argument with Dmitrii Ostrovskii. See the end of the post)

Studying eigenvalues of covariance operators. From now on, we only consider covariance operators and our goal is to understand their spectral properties. In these blog posts, we will consider two domains \(\mathcal{X}\) of interest: the \(d\)-dimensional torus (that is, \([0,\! 1]^d\) with periodicity conditions) and \(\mathbb{R}^d\), both with translation-invariant kernels. The first one in this blog post because everything will be easy to deal with (with exact expressions for eigenvalues), the second in the next post because it is ubiquitous in practice but requires finer tools to characterize asymptotic behaviors.

Periodic translation-invariant kernels on \([0,\! 1]\)

We consider kernel functions on \(\mathcal{X} = [0,\! 1]\) that depend only on the fractional part of \(x-y\), that is, $$k(x,y) = q(x-y),$$ for a \(1\)-periodic function \(q\). What makes everything easy in this situation, is that the (complex-valued) functions \(x \mapsto e^{2i\pi\omega x}\), for \(\omega \in \mathbb{Z}\), form an orthonormal basis of \(L_2([0,1])\), so that we have the decomposition $$k(x,y) = \sum_{\omega \in \mathbb{Z}} \hat{q}_\omega e^{2i\pi\omega (x-y)}= \sum_{\omega \in \mathbb{Z}} \hat{q}_\omega e^{2i\pi \omega x} (e^{2i\pi \omega y})^\ast. $$ Thus, the square-integrable eigenfunctions are \(g_\omega(x) = e^{2i\pi \omega x}\) for \(\omega \in \mathbb{Z}\) (they are thus exactly equal to \(1\) in magnitude), and eigenvalues of the covariance operators are exactly the Fourier coefficients \( \hat{q}_\omega \in \mathbb{R}_+\). In order to have a real-valued symmetric kernel function, for all \(\omega \in \mathbb{Z}\), \(\hat{q}_{-\omega} = \hat{q}_\omega\), and thus, if the Fourier series is decreasing in \(|\omega|\), the sequence of eigenvalues is $$\hat{q}_{0}, \hat{q}_{1},\hat{q}_{1}, \hat{q}_{2},\hat{q}_{2}, \dots,$$ with thus eigenvalues coming at least by pairs (except the first one).

It is not the topic of today, but the spectral decay is associated to the characterization of the norm of \(\theta\) when a function \(f\) can be represented as \(f(x) = \langle \theta, \varphi(x) \rangle\). This norm depends precisely on the \(L_2\)-norms of derivatives of \(f\) (see [22] and [1, Chapter 7]).

In order to have a nice list of examples, we can easily go back and forth between \(q\) and its Fourier coefficients \((\hat{q}_\omega)_{\omega \in \mathbb{Z}}\) for a variety of situations. Below we start with \(\hat{q}\) and give the expression of \(q\).

• Bernoulli polynomials: \(\hat{q}_0 = \pi^2/3\), \(\hat{q}_\omega = |\omega|^{-2s}\) when \(\omega \neq 0\), for \(s\) strictly positive integer. We can then show that (see, e.g., [22]) $$q(x) = \frac{\pi^2}{3} + (-1)^{s-1} \frac{(2\pi)^{2s}}{(2s)!}B_{2s}(\{x\}),$$ where \(\{x\} = x – \lfloor x \rfloor \in [0,1)\) is the fractional part of \(x\), and \(B_{2s}\) the \((2s)\)-th Bernoulli polynomial. For example, for \(s=1\), we obtain \(q(x) = \frac{\pi^2}{3} – 2\pi^2 \{x\} + 2\pi^2 \{x\}^2\), which is a degree-two polynomial in \(\{x\}\). These kernels are useful to study different decays of eigenvalues of the form \(m^{-\alpha}\) for \(\alpha\) an even integer.
• Hyperbolic functions: \(\hat{q}(\omega) = \frac{1}{1+\omega^2 \alpha^2}\), with then the explicit formula (obtained in an earlier blog post on residue calculus): $$q(x) = \frac{\pi/\alpha}{\sinh (\pi/\alpha)} \cosh \big(\frac{\pi}{\alpha} (1 – 2 | \{t+1/2\}\!-\! 1/2| ) \big).$$ This kernel is useful as it leads to a Sobolev space with squared norm which is explicitly the sum of \(L_2\)-derivatives of the function and its derivative, and thus related to the Abel kernel.
• Exponential decay: \(\hat{q}(\omega) = \rho^{|\omega|}\) for \(\rho \in (0,1)\), for which we have by using sums of geometric series: $$q(x) = \frac{1-\rho^2}{1+\rho^2 \, – 2\rho \cos(2\pi x)}.\tag{2}$$

We can now extend the one-dimensional torus \([0,\! 1]\) to \(d\) dimensions.

From \([0,\! 1]\) to \([0,\! 1]^d\)

We consider kernels of the form \(k(x,y)=q(x-y)\) for \(q\) a \(1\)-periodic function, that is, for which \(q(x+z)=q(x)\) for any vector \(z \in \mathbb{Z}^d\). For the uniform distribution on \([0,\! 1]^d\), like in one dimension, the functions \(x \mapsto e^{2i\pi \omega^\top x}\), for \(\omega \in \mathbb{Z}^d\), form an orthonormal basis of square-integrable functions. By using multi-dimensional Fourier series, we can decompose $$q(x) = \sum_{\omega \in \mathbb{Z}^d} \hat{q}_\omega e^{2i\pi\omega^\top(x-y)}.$$ Eigenvalues are then \(\hat{q}_\omega\) for \(\omega \in \mathbb{Z}^d\). Thus, eigenvalues also come at least by pairs, as we also have \(\hat{q}_{-\omega} = \hat{q}_\omega\), but as we will see below, they can coalesce even more.

A particularly interesting and common case corresponds to product kernels of the form $$\hat{q}_\omega = \prod_{j=1}^d \hat{r}_{\omega_j},$$ where \(r\) is a positive definite function on \([0,\! 1]\) (that is, \(\hat{r}_\omega \geqslant 0\) for all \(\omega \in \mathbb{Z}\)), since then $$q(x) = \prod_{j=1}^d r(x_j).$$ Depending on the Fourier series \((\hat{r}_{\omega})_{\omega \in \mathbb{Z}}\), eigenvalues can coalesce beyond coming by pairs. For example, when \(\hat{r}_{\omega}= \rho^{|\omega|}\), then eigenvalues of \(\Sigma\) are \(\rho^{\| \omega \|_1}\), where \(\| \omega \|_1\) is the \(\ell_1\)-norm of \(\omega\). Thus, all eigenvalues have a known multiplicity, that is, the eigenvalue \(\rho^{r}\) for \(r\) non-negative integer, has a multiplicity equal to the number \(n(d,r)\) of \(\omega \in \mathbb{Z}^d\) such that \(\|\omega\|_1 = r\). For \(d=1\), we recover the sequence above, since \(n(1,0)=1\) and \(n(1,r)=2\) for \(r\geqslant 1\). When \(d \geqslant 1\), I am not aware of a general formula (please let me know if you know one, see [23] for some results), but one can show (see the end of the post) that \(n(d,r) \sim 2^r { d \choose r}\) when \(d \to +\infty\), and \(n(d,r)\sim \frac{2^d}{(d-1)!} r^{d-1}\) when \(r \to +\infty\). We then obtain the eigenvalues plotted below, where we see the various discrete levels. Note that here \(\log \frac{1}{\lambda_m}\) is of order \(\log \frac{1}{\rho} \cdot m^{1/d}\) (see [9, Section 2.3]).

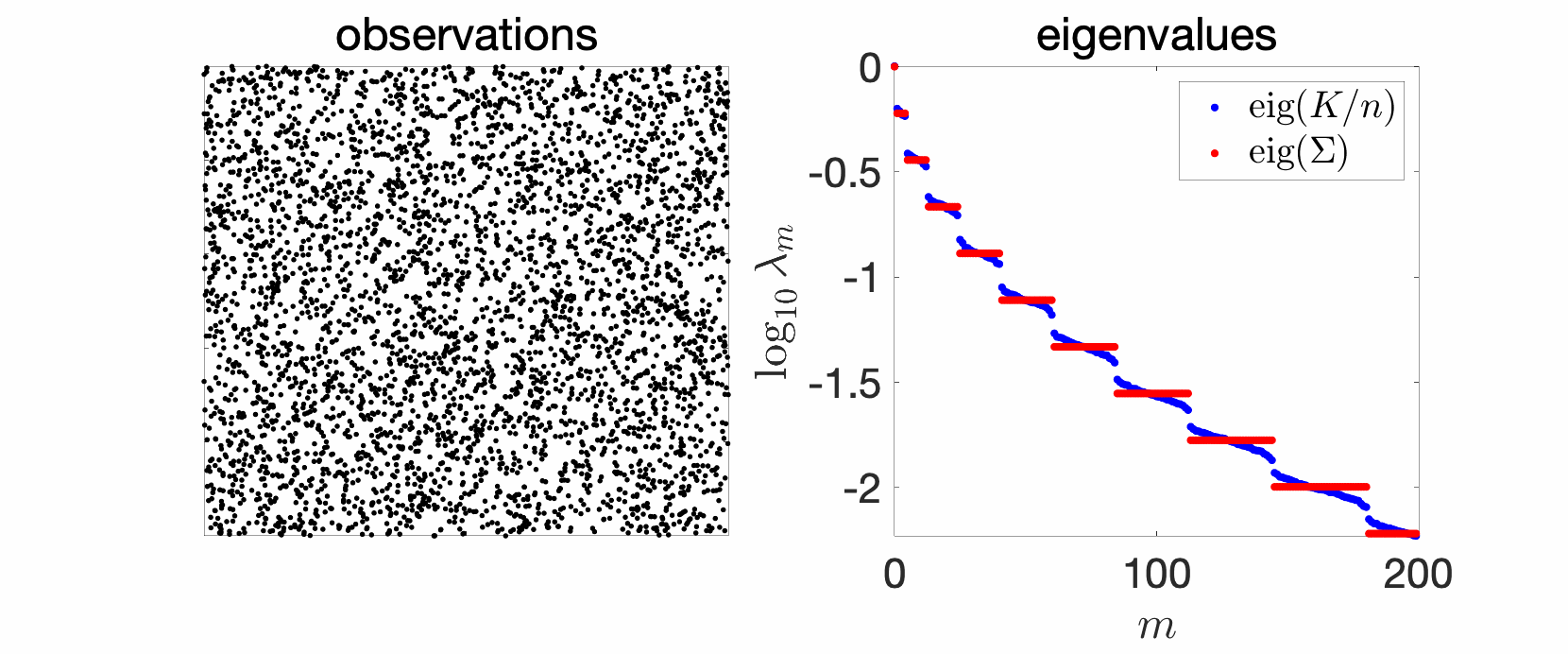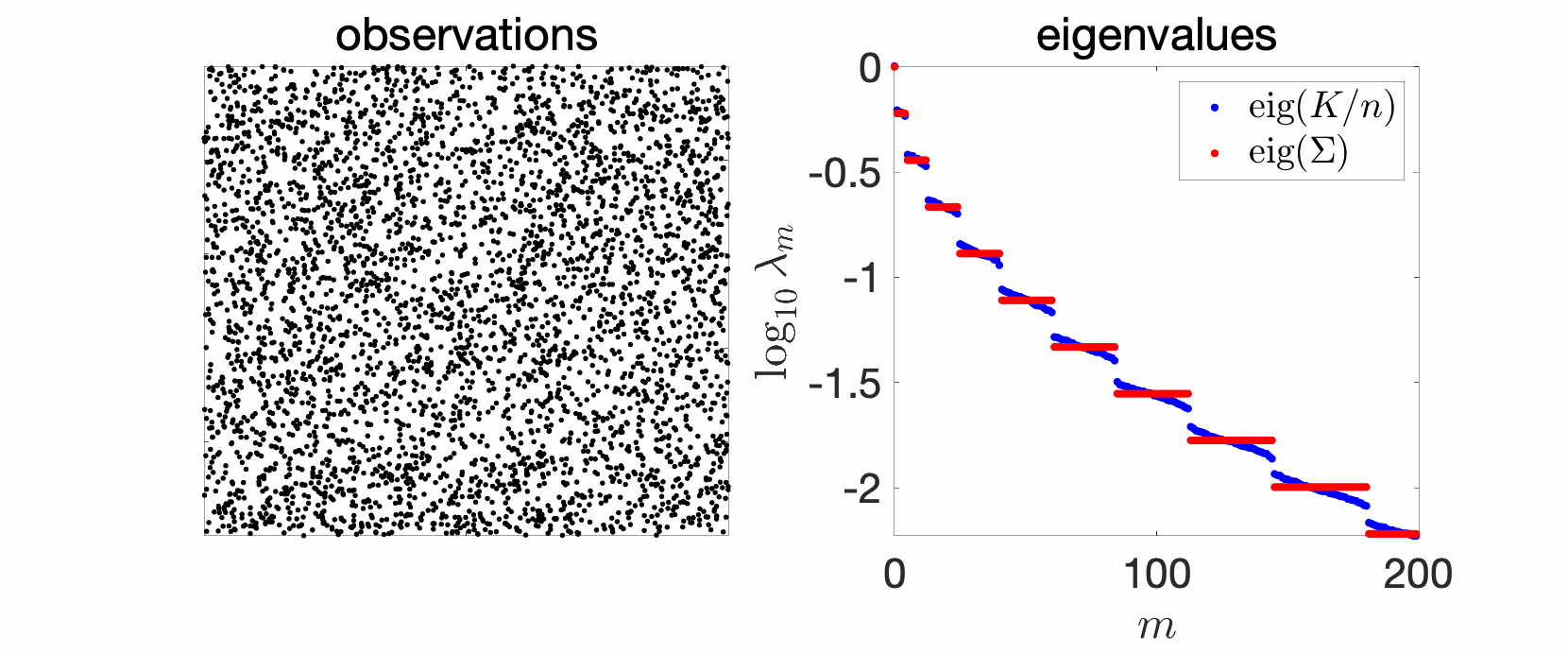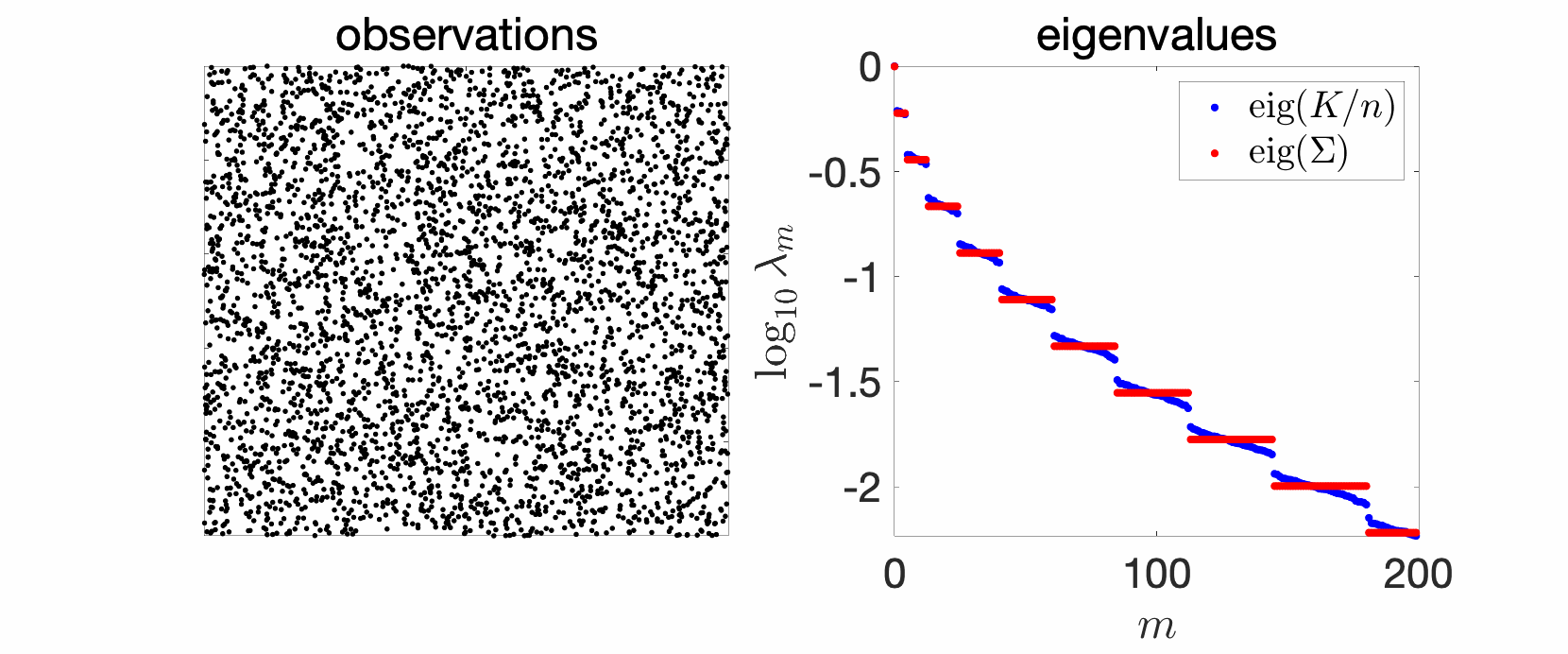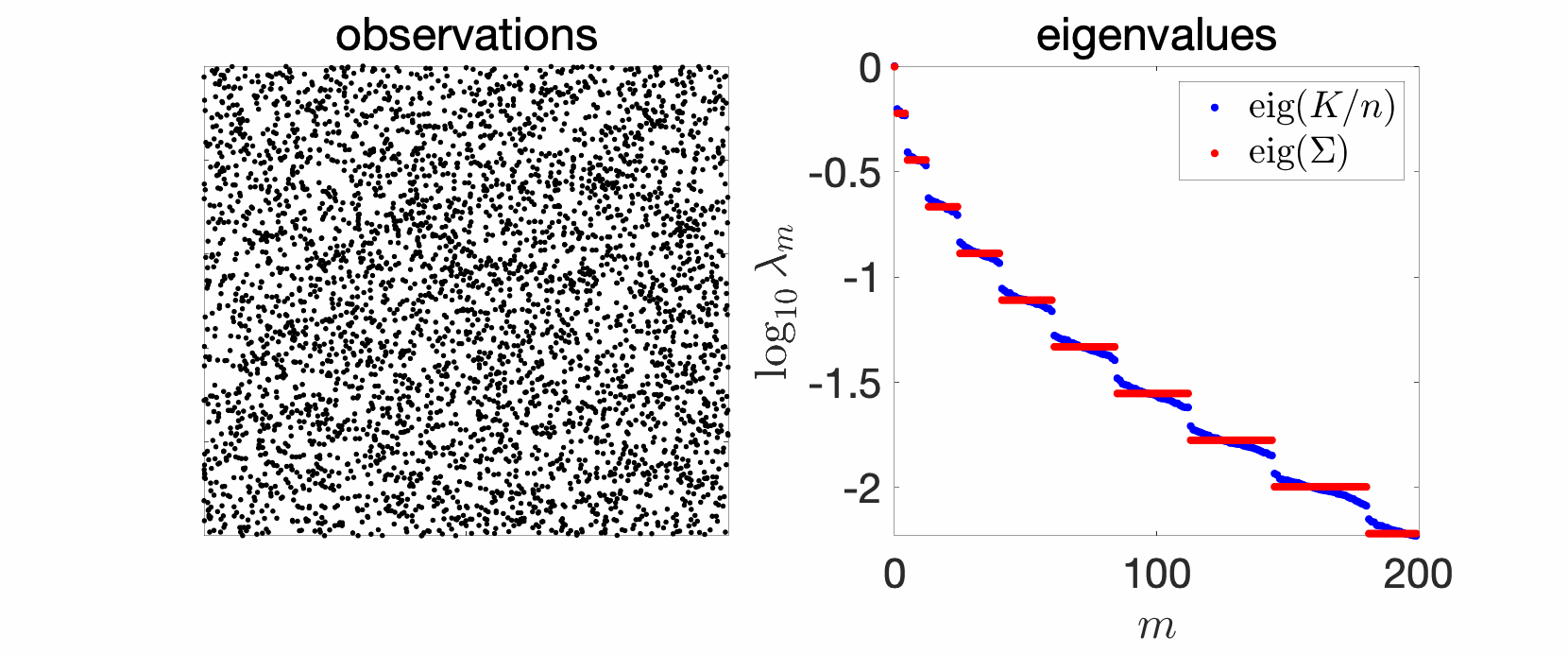
For the Fourier series \(\hat{r}_\omega = {1}/ (1\!+\!|\omega|^2)\), eigenvalues coalesce less, as shown below. It is however possible to show that \(\lambda_m\) is of order \({(\log m)^2}/{m^2}\) (see [9, Section 2.3]).

Conclusion

In this blog post, we first showed how large kernel matrices had eigenvalues that tend to the eigenvalues of the (typically infinite-dimensional) covariance operator, at rate \(O(1/\sqrt{n})\) where \(n\) is the number of observations, with a new improved multiplicative bound for smaller eigenvalues.

We then studied a class of pairs (kernel, input distribution) that led to exact expressions for these eigenvalues, namely, translation-invariant kernels on \([0,\! 1]^d\). However, these kernels are rarely used in practice. The goal of the next blog post will be to consider generic probability distributions on \(\mathbb{R}^d\) and translation-invariant kernels of the form \(k(x,y) =q(x-y)\) with \(q\) a function with non-negative Fourier transform. No closed form any more in general (except for Gaussians), so not as easy, but nice approximations are possible!

References

[1] Francis Bach. Learning Theory from First principles. Book draft, 2024.
[2] Christopher Williams, Matthias Seeger. Using the Nyström method to speed up kernel machines. Advances in Neural Information Processing Systems, 2000.
[3] Shai Fine, Katya Scheinberg. Efficient SVM training using low-rank kernel representations. Journal of Machine Learning Research, 2:243-264, 2001.
[4] Francis Bach, Michael I. Jordan. Kernel independent component analysis. Journal of Machine Learning Research, 3:1-48, 2002.
[5] Michael W. Mahoney, Petros Drineas. CUR matrix decompositions for improved data analysis. Proceedings of the National Academy of Sciences, 106(3):697-702, 2009.
[6] Ali Rahimi, Benjamin Recht. Random features for large-scale kernel machines. Advances in Neural Information Processing Systems, 2007.
[7] Francis Bach. Sharp analysis of low-rank kernel matrix approximations. Conference on learning theory, 2013.
[8] Ahmed El Alaoui, Michael W. Mahoney. Fast randomized kernel ridge regression with statistical guarantees. Advances in Neural Information Processing Systems, 2015.
[9] Francis Bach. On the equivalence between kernel quadrature rules and random feature expansions. Journal of Machine Learning Research, 18(1):714-751, 2017.
[10] Alessandro Rudi, Lorenzo Rosasco. Generalization properties of learning with random features. Advances in Neural Information Processing Systems, 2017.
[11] Aymeric Dieuleveut, Nicolas Flammarion, Francis Bach. Harder, Better, Faster, Stronger Convergence Rates for Least-Squares Regression. Journal of Machine Learning Research, 18(101):1-51, 2017.
[12] Raphaël Berthier, Francis Bach, Pierre Gaillard. Accelerated Gossip in Networks of Given Dimension using Jacobi Polynomial Iterations. SIAM Journal on Mathematics of Data Science, 2(1):24-47, 2020.
[13] Fabian Pedregosa, Damien Scieur. Acceleration through spectral density estimation. International Conference on Machine Learning, 2020.
[14] Noureddine El Karoui. The Spectrum of Kernel Random Matrices. Annals of Statistics, 38(1): 1-50, 2010.
[15] Simon Barthelmé, Konstantin Usevich. Spectral properties of kernel matrices in the flat limit. SIAM Journal on Matrix Analysis and Applications, 42(1):17-57, 2021.
[16] Andrea Caponnetto, Ernesto De Vito. Optimal rates for the regularized least-squares algorithm. Foundations of Computational Mathematics, 7:331-368, 2007.
[17] Bhatia, Rajendra, Ludwig Elsner. The Hoffman-Wielandt inequality in infinite dimensions. Proceedings of the Indian Academy of Sciences (Mathematical Sciences), 104(3):483:494, 1994.
[18] Stanislav Minsker. On some extensions of Bernstein’s inequality for self-adjoint operators. Statistics and Probability Letters, 127:111-119, 2017.
[19] Joell A. Tropp. An Introduction to Matrix Concentration Inequalities. Foundations and Trends in Machine Learning, 8(1-2):1-230, 2015.
[20] Mikio L. Braun. Accurate error bounds for the eigenvalues of the kernel matrix. Journal of Machine Learning Research, 7:2303-2328, 2006.
[21] Vladimir Koltchinskii and Evarist Giné. Random matrix approximation of spectra of integral operators. Bernoulli, 6(1):113–167, 2000.
[22] Grace Wahba. Spline Models for Observational Data. Society for industrial and applied mathematics, 1990.
[23] Patrick Solé. Counting lattice points in pyramids. Discrete mathematics, 139(1-3): 381-392, 1995.
[24] Francis Bach. Information theory with kernel methods. IEEE Transactions on Information Theory, 69(2):752-775, 2022.
[25] Dmitrii M. Ostrovskii, Alessandro Rudi. Affine invariant covariance estimation for heavy-tailed distributions. Conference on Learning Theory, 2019.

Infinite-dimensional bound on operator norm

Given a feature map \(\varphi: \mathcal{X} \to \mathcal{H}\) such that \(\| \varphi(x)\| \leqslant R\) almost surely. We have from [19, Theorem 7.7.1], for any \(\delta \in (0,1)\), with probability greater than \(1 – \delta\): $$ \| \Sigma\, – \hat\Sigma \|_{\rm op} \leqslant \frac{2R^2}{3n} \log \frac{8d}{\delta} + \sqrt{ \frac{2R^2}{n} \| \Sigma\|_{\rm op} \log \frac{8d}{\delta}},$$ with \(d = \frac{ {\rm tr}(\Sigma)}{\| \Sigma\|_{\rm op}}\) is referred to as the intrinsic dimension of \(\Sigma\) (as originally defined by [18]). This already leads to an improved bound compared to the Hilbert-Schmidt one we proposed earlier.

Moreover, this is often applied to \((\Sigma+\lambda I)^{-1/2} \varphi\) (see, e.g., [10]), leading to, with a probability greater than \(1-\delta\): $$\| (\Sigma+\lambda I)^{-1/2} ( \Sigma\, – \hat\Sigma) (\Sigma+\lambda I)^{-1/2}\|_{\rm op} \leqslant \frac{2 {\rm df}(\lambda) }{3n} \log \frac{8d}{\delta} + \sqrt{ \frac{2{\rm df}(\lambda)}{n} \log \frac{8d}{\delta}},$$ with \(d = {\rm df}(\lambda) \big( 1 + \frac{\lambda}{\| \Sigma\|_{\rm op} }\big) \leqslant \frac{R^2}{\lambda} \big( 1 + \frac{\lambda}{\| \Sigma\|_{\rm op} }\big) \leqslant \frac{2R^2}{\lambda}\) if \(\lambda \leqslant \| \Sigma\|_{\rm op}\), where we already defined the maximal degrees of freedom as \({\rm df}(\lambda) = \sup_{x \in \mathcal{X}} \langle \varphi(x), (\Sigma+\lambda I)^{-1} \varphi(x) \rangle\). Under regularity conditions explained in the post (bounded eigenfunctions), \({\rm df}(\lambda)\) has the same order as the regular degrees of freedom \({\rm tr} [ \Sigma(\Sigma+\lambda I)^{-1} ]\) when \(\lambda\) tends to zero. The dominant term is then \( \sqrt{ \frac{{\rm df}(\lambda)}{n}}\) up to logarithmic terms.

Multiplicative eigenvalue bounds

We aim to bound \(\| \log (\Sigma \!+\! \lambda I)- \log (\hat \Sigma \!+\! \lambda I)\|_{\rm op}\) by \(\varepsilon\), which will lead to a bound of the form $$| \log( \lambda_m(\Sigma)\!+\!\lambda)\, – \log( \lambda_m(\hat\Sigma)\!+\!\lambda)| \leqslant \| \log (\Sigma \!+\! \lambda I)- \log (\hat \Sigma \!+\! \lambda I)\|_{\rm op} \leqslant \varepsilon,$$ which in turn leads to bounds for each eigenvalues: $$ | \lambda_m(\Sigma) \, – \lambda_m(\hat\Sigma) | \leqslant (\lambda_m(\Sigma) +\lambda) ( e^\varepsilon – 1),$$ which are multiplicative up to the factor \(\lambda\). Since, up to logarithmic factors, \(\varepsilon \approx \sqrt{ \frac{{\rm df}(\lambda)}{n}}\), we get (up to logarithmic terms) $$ | \lambda_m(\Sigma) \, – \lambda_m(\hat\Sigma) | \leqslant (\lambda_m(\Sigma) +\lambda) \sqrt{ \frac{{\rm df}(\lambda)}{n}}.$$ Thus, overall, it all depends on how \({\rm df}(\lambda)\) tends to infinity when \(\lambda\) tends to zero, which is exactly what can be obtained from results in this and next blog post. A natural choice is \(\lambda \sim \lambda_m(\Sigma)\), and for “well-behaved” cases (such as \(\lambda_m \sim C m^{-\alpha}\)), then \({\rm df}(\lambda_m) \sim m\), leading to the multiplicative bound \(| \lambda_m(\Sigma) \, – \lambda_m(\hat\Sigma) | \leqslant \lambda_m(\Sigma) \sqrt{ \frac{m}{n}}\), which is an improvement over results [20], that do not lead to multiplicative bounds in \(O(1/\sqrt{n})\).

Details of the bound. We assume that \(\lambda\) is chosen so that \(\lambda \leqslant \| \Sigma\|_{\rm op} \leqslant R^2\), \(n \geqslant 9\), and $$\frac{{\rm df}(\lambda) }{n} \cdot \log \frac{16 R^2}{ \lambda \delta} \cdot \big( \log \frac{R^2 \sqrt{n}}{\lambda} \big)^2 \leqslant \frac{1}{8}.$$

This is possible as soon \(\frac{1}{n} \frac{R^2}{\| \Sigma \|_{\rm op}} \cdot \log \frac{16 R^2}{ \| \Sigma \|_{\rm op} \delta} \big( \log \frac{R^2 \sqrt{n}}{\| \Sigma \|_{\rm op}} \big)^2 \leqslant \frac{1}{8}\), and thus for \(n\) large enough. Note also that this implies \({\rm df}(\lambda) \geqslant 1/2\).

This first implies from the bound above that with probability greater than \(1-\delta\), $$\| (\Sigma\!+\!\lambda I)^{-1/2} ( \Sigma\, – \hat\Sigma) (\Sigma\!+\! \lambda I)^{-1/2}\|_{\rm op} \leqslant t, \tag{3}$$ with \(t \leqslant \frac{3}{4}\) and \(t \leqslant 2 \sqrt{ \frac{{\rm df}(\lambda)}{n} \log \frac{16 R^2}{ \lambda \delta}}\).

We then have by an integration which is similar to the proof of operator monotonicity of the logarithm (see this post) and already used in a similar context in [24], $$ \log (\Sigma \!+\! \lambda I) \, – \log (\hat\Sigma \!+\! \lambda I) = \int_\lambda^{\infty} \big[ (\hat\Sigma \!+\! \mu I)^{-1} – (\Sigma \!+\! \mu I)^{-1} \big] d\mu.$$ In order to bound the integrand above, we use the classical identity $$ (\hat\Sigma \!+\! \mu I)^{-1} – (\Sigma \!+\! \mu I)^{-1} = (\hat\Sigma \!+\! \mu I)^{-1} (\Sigma \, – \hat\Sigma) (\Sigma \!+\! \mu I)^{-1}, $$ and the associated bound $$\| (\hat\Sigma \!+\! \mu I)^{-1} – (\Sigma \!+\! \mu I)^{-1}\|_{\rm op} \leqslant \frac{1}{\mu} \| (\hat\Sigma \!+\! \mu I)^{-1/2} (\Sigma \, – \hat\Sigma) (\Sigma \!+\! \mu I)^{-1/2}\|_{\rm op}.$$ We can now use our approximation in Eq. \((3)\) with \(t \leqslant \frac{3}{4}\) in a standard way in the analysis of kernel methods (see,e.g., [10]), that is, $$ \| (\hat\Sigma \!+\! \mu I)^{-1/2} (\Sigma \!+\! \mu I)^{1/2} \|_{\rm op} \leqslant \frac{1}{\sqrt{1-t}} \leqslant 2.$$ Thus, for \(\mu \in [\lambda, R^2 \sqrt{n}]\), we can bound $$\| (\hat\Sigma + \mu I)^{-1} – (\Sigma + \mu I)^{-1} \|_{\rm op} \leqslant \frac{1}{\mu} \frac{t}{\sqrt{1-t}} \leqslant \frac{2 t}{\mu},$$ while for \(\mu \geqslant R^2 \sqrt{n}\), we bound $$\| (\hat\Sigma \!+\! \mu I)^{-1} – (\Sigma \!+\! \mu I)^{-1} \|_{\rm op} \leqslant \frac{1}{\mu^2} \|\hat\Sigma-\Sigma\|_{\rm op} \leqslant \frac{2R^2}{\mu^2}. $$ Thus, by integrating the bounds and using the triangular inequality, we get: $$\| \log (\Sigma \!+\! \lambda I) \, – \log (\hat\Sigma \!+\! \lambda I)\|_{\rm op} \leqslant \int_\lambda^{R^2\sqrt{n}} \frac{2t}{\mu}d\mu + \int_{R^2\sqrt{n}}\frac{2R^2}{\mu^2} d\mu.$$ This leads to $$\| \log (\Sigma + \lambda I) \, – \log (\hat\Sigma + \lambda I)\|_{\rm op} \leqslant {2t} \log \frac{R^2 \sqrt{n}}{\lambda} + \frac{2}{\sqrt{n}}.$$ We thus get the bound using Eq. \((3)\) $$\| \log (\Sigma + \lambda I) \, – \log (\hat\Sigma + \lambda I)\|_{\rm op} \leqslant \frac{1}{\sqrt{n}} \big( 2 + 2 \log \frac{R^2 \sqrt{n}}{\lambda} \sqrt{ {\rm df}(\lambda) \log\frac{16 R^2}{ \lambda \delta} }\big).$$ Thus, since we have assumed that \(n \geqslant 9\) and $$ \frac{{\rm df}(\lambda) }{n} \cdot \log\frac{16 R^2}{ \lambda \delta} \cdot \big(\! \log \frac{R^2 \sqrt{n}}{\lambda} \big)^2 \leqslant 1/8,$$ the bound above is less than \(2/3 + \sqrt{2}/2 \leqslant 3/2\), so that the value \(\varepsilon\) above is less than \(3/2\), which implies that \(e^\varepsilon – 1 \leqslant (5/2) \varepsilon\). Using that all logarithmic terms are greater than \(1\), and that \({\rm df}(\lambda) \geqslant 1/2\), we then obtain the bound $$ | \lambda_m(\Sigma) \, – \lambda_m(\hat\Sigma) | \leqslant 9 (\lambda_m(\Sigma) +\lambda)\sqrt{\frac{{\rm df}(\lambda) }{n}} \cdot\log \frac{R^2 \sqrt{n}}{\lambda} \cdot \sqrt{ \log \frac{16 R^2}{ \lambda \delta}}.$$

(added January 9, 2024) Simpler argument. As mentioned to me by Alessandro, there is a simpler way of obtaining a slightly sharper result coming from [25, Corollary 12]. Starting from Eq. \((3)\), we get $$ -t ( \Sigma \! + \! \lambda I) \preccurlyeq \hat{\Sigma} \, – \Sigma \preccurlyeq t ( \Sigma \! + \! \lambda I),$$ which directly implies that for all \(m \geqslant 0\), $$ -t ( \lambda_m(\Sigma) \! + \! \lambda ) \leqslant \lambda_m(\hat{\Sigma}) \, – \lambda_m(\Sigma) \leqslant t ( \lambda_m(\Sigma) \! + \! \lambda),$$ and thus \(| \lambda_m(\hat{\Sigma}) \, – \lambda_m(\Sigma)| \leqslant ( \lambda_m(\Sigma) \! + \! \lambda) \cdot 2 \sqrt{ \frac{{\rm df}(\lambda)}{n}} \cdot \sqrt{ \log \frac{16 R^2}{ \lambda \delta}}.\)

Analysis of \(n(d,r)\)

As defined above, \(n(d,r)\) is the number of \(\omega \in \mathbb{Z}^d\) such that \(\|\omega\|_1 = r\). We have by direct inspection \(n(d,0)=1\) and \(n(d,1) = 2d\) for all \(d \geqslant 1\). We can use the classical result that the number of \(\omega \in \mathbb{N}^d\) such that \(\|\omega\|_1 = r\) (that is only non-negative integers) is equal to \({ d+s-1 \choose d-1}\), and isolate the set \(A \subset \{1,\dots,d\}\) for which the components of \(\omega\) are strictly positive, we then get: $$n(d,r)=\sum_{A \subset \{1,\dots,d\}, \, 1 \leqslant |A| \leqslant s} 2^{|A|}{ s-1 \choose |A|-1}=\sum_{k=1}^s 2^k { s-1 \choose k-1} { d \choose k}.$$

From the expansion above, we get the equivalent \(n(d,r) \sim 2^r { d \choose r}\) when \(d \to +\infty\). In order to obtain the equivalent \(n(d,r)\sim \frac{2^d}{(d-1)!} r^{d-1}\) when \(r \to +\infty\), we can derive a recursion between \(n(d,r)\) and the values \(n(d-1,s)\) for \(s \leqslant r\), that is, for \(r\geqslant 1\), $$n(d,r) = 2 + n(d-1,r) + 2 \sum_{s=1}^{r-1} n(d-1,s),$$ which can be obtained by looking at all potential values of \(|\omega_d|\), from \(0\) to \(r\).