Acceleration without pain

I don’t know of any user of iterative algorithms who has not complained one day about their convergence speed. Whether the data are too big, the processors not fast or numerous enough, waiting for an algorithm to converge unfortunately remains a core practical component of computer science and applied mathematics. This was already a concern long before computers were invented (and most of the techniques I will describe date back to the early 19th century): imagine you are doing all the operations (multiplications, additions, divisions) by hand, wouldn’t you want some cheap way to accelerate your algorithm (and here literally reduce your pain)?

Acceleration is a key concept in numerical analysis and can be carried through in two main ways. The first way is to modify some steps of the algorithm (such as Nesterov acceleration for gradient descent, or Chebyshev / Jacobi acceleration for linear recursions). This requires a good knowledge of the inner structure of the underlying algorithm. A second way is to totally ignore the specifics of the algorithm, and see the acceleration problem as trying to find good “combinations” of the observed iterates that converge faster.

In this blog post, I thus consider a sequence of iterates \((x_k)_{k \geq 0}\) in \(\mathbb{R}^d\) obtained from an iterative algorithm \(x_{k+1} = T(x_k)\), which will typically be an optimization algorithm. The main question I will address is: Can we do better than outputting the last iterate?

This has a long history in numerical analysis, where many techniques have been developed for uni-dimensional sequences. Acceleration techniques vary according to the type of convergence of the original sequence (quadratic, linear, sublinear), the amount of knowledge about the asymptotic behavior, and the possibility of extensions to high-dimensional and noisy problems.

Acceleration techniques are often based on an explicit or implicit modelling of the sequence \(x_k\), either through a model of the function \(T: \mathbb{R}^d \to \mathbb{R}^d\) (the iteration of the algorithm) or through an asymptotic expansion of \(x_k\). In this post, I will focus on linearly convergent sequences, that is, sequences \(x_k\) converging to some \(x_\ast\) at an exponential rate. As we will see, this will done through modelling \(x_k\) as an autoregressive process.

I will first start from the simplest scheme, the Aitken’s \(\Delta^2\) process from 1926 [1], then look at higher order generalizations still in one dimension, and finally to the general vector case. We will then apply all that to gradient descent.

Aitken’s \(\Delta^2\) process

This is the simplest of all techniques and the source of all others in this post. We try to model \(x_k\in \mathbb{R}\) as first-order auto-regressive sequence, that is, \(x_{k+1} = ax_{k}+b\), for \(a,b \in \mathbb{R}\). The method works by (a) estimating \(a\) and \(b\) from a sequence of few consecutive (here three) iterates, and (b) extrapolating by computing the limit \(x_{\rm acc}\) of the estimated model. Given that we fit the model to consecutive iterates \((x_k,x_{k+1},x_{k+2})\), the model \((a,b)\) will also depend on \(k\), as well as its limit \(x_{\rm acc}\). In order to avoid having too many \(k\)’s in my notations, I will drop the dependence in \(k\) of the model parameters.

In this situation, the model recursion has a limit when \(a \neq 1\), and the limit is \(x_{\rm acc} = \frac{b}{1-a}\). In order to fit the two parameters, we need two equations, which can be obtained by considering two consecutive evaluations of the recursions (which require three iterates). That is, we consider the linear system in \((a,b)\): $$ \Big\{ \begin{array}{ll} ax_{k}+b & = x_{k+1} \\ ax_{k+1}+b & = x_{k+2} \end{array}$$ which can be solved in a variety of ways. All of them are equivalent, but naturally lead to different extensions.

Solving by elimination. We can eliminate \(b\) by subtracting the two equations, leading to $$ x_{k+2} – x_{k+1} = a ( x_{k+1} – x_{k}),$$ and thus $$a = \frac{ x_{k+2} – x_{k+1}}{ x_{k+1} – x_{k}}.$$ We then get $$b = x_{k+1} – a x_{k} = x_{k+1} – \frac{ x_{k+2} – x_{k+1}}{ x_{k+1} – x_{k}} x_{k} = \frac{ x_{k+1}^2 – x_{k} x_{k+2}}{ x_{k+1} – x_{k}}, $$ and the extrapolating sequence $$x_{\rm acc} = \frac{b}{1-a} = \frac{x_{k} x_{k+2} – x_{k+1}^2 }{-2 x_{k+1} + x_{k+2} + x_{k}},$$ which we denote \(x^{(1)}_k\), to highlight its dependence on \(k\). Note that to compute \(x^{(1)}_k\), we need access to the three iterates \((x_k,x_{k+1},x_{k+2})\), and thus, when comparing the original sequence to the extrapolated one, we will compare \(x_k\) and \(x^{(1)}_{k-2}\).

Asymptotic auto-regressive model. A key feature of the acceleration techniques that I describe in this post is that although they implicitly or explicitly model sequence with auto-regressive processes, the models do not need to be correct, that is, they also work if the autoregressive recursion is true only asymptotically, for example \(\displaystyle \frac{x_{k+1}-x_\ast}{x_k – x_\ast}\) converging to a constant \(a \in [-1,1)\). Then we also get some acceleration, which can be quantified (see the end of the post for details), and for which we present a classical example below.

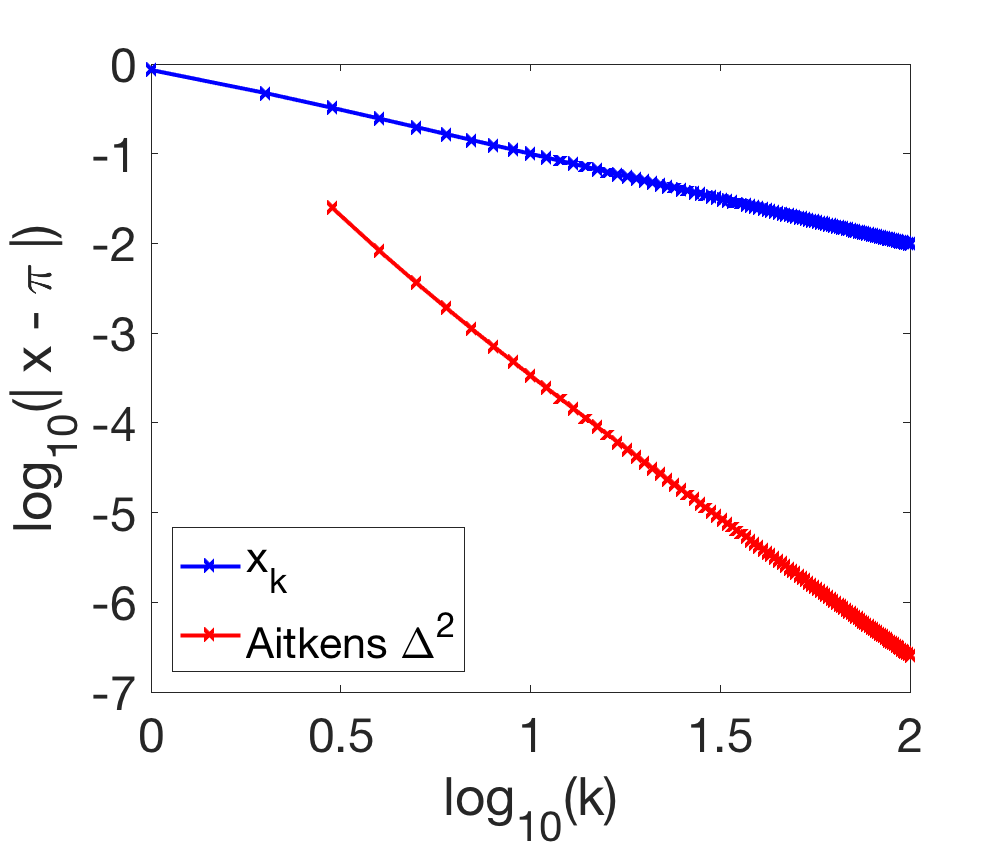
Approximating \(\pi\). We consider the Leibniz formula, which is one of many ways of approximating \(\pi\): $$ \pi = \lim_{k \to +\infty} x_k \mbox{ with } x_k = 4 \sum_{i=0}^{k} \frac{(-1)^i}{2i+1}.$$ This formula can be proved by expanding the derivative \(x \mapsto \frac{1}{1+x^2}\) of \(x \mapsto \arctan x\) as a power series and then integrating it. We can check that $$\frac{x_{k+1}-x_\ast}{x_k – x_\ast} = \ – 1 + \frac{1}{k} + o( \frac{1}{k}), $$ and as detailed at the end of the post, we should expect the error to go from \(1/k\) to \(1/k^3\). Below, we show the first 10 iterates of the two sequences, with the correct significant digits in bold. $$ \begin{array}{|l|l|l|} \hline k & x_k & x_k^{(1)} \\ \hline 1 & 4.0000 & \times \\ 2 & 2.6667 & \times \\ 3 & \mathbf{3}.4667 & \mathbf{3.1}667 \\ 4 & 2.8952 & \mathbf{3.1}333 \\ 5 & \mathbf{3}.3397 & \mathbf{3.14}52 \\ 6 & 2.9760 & \mathbf{3.1}397 \\ 7 & \mathbf{3}.2837 & \mathbf{3.14}27 \\ 8 & \mathbf{3}.0171 & \mathbf{3.14}09 \\ 9 & \mathbf{3}.2524 & \mathbf{3.14}21 \\ 10 & \mathbf{3}.0418 & \mathbf{3.141}3 \\ \hline \end{array}$$ We see that the extrapolated sequence converges much faster. This is confirmed in the convergence plot below:

Higher-order one-dimensional extensions

The Aitken’s \(\Delta^2\) process relies on fitting a first-order auto-regressive model, or on assuming that \(x_{k+1} – x_\ast – a (x_k – x_\ast) \to 0\) asymptotically. This can be extended to \(m\)-th order constant recursions. This corresponds to modelling \(x_k\) as the sum of \(m\) exponentials.

We thus try to fit the model $$x_{k+m} = a_0 x_k + a_1 x_{k+1} + \cdots + a_{m-1} x_{k+m-1} + b = \sum_{i=0}^{m-1} a_i x_{k+i} + b, $$ which has \(m+1\) parameters. We thus need \(m + 1\) equations, that is we consider the recursion for \(k, k+1,\dots, k+m\), which requires the knowledge of the \(2m+1\) iterates \(x_k, x_{k+1},\dots,x_{k+2m}\). This leads to the \(m+1\) equations: $$x_{k+m+j} = a_0 x_{k+j} + a_1 x_{k+j+1} + \cdots + a_{m-1} x_{k+j+m-1} + b = \sum_{i=0}^{m-1} a_i x_{k+j+i} + b,$$ for \(j \in \{0,\dots,m\}\). This is a system with \(m+1\) unknowns and \(m+1\) equations, from which we could get all \(a_j\)’s and \(b\), and then the model limit as the extrapolated sequence \(x^{(m)}_k = \frac{b}{1 – a_0 – a_1 – \cdots – a_{m-1}}\).

This linear system can be solved in a variety of ways. At the end of the blog post, I show how it can be solved using determinants of Hankel-like matrices, often referred to as the Shanks transformation, which then leads to an iterative algorithm dating back from Wynn [2], which is called the \(\varepsilon\)-algorithm. In order to smooth our way to the vector case extension, I will present it in a slightly non-standard way. See [3] for detailed surveys on acceleration and extrapolation, and their rich history.

Instead of learning the model parameters to estimate \(x_{k+m}\) from the past iterates, we focus directly on the prediction of the limit \(x_{\rm acc}\) by looking for real numbers \(c_0,\dots,c_m\) such that for all \(k\), $$\sum_{i=0}^m c_i ( x_{k+i} – x_{\rm acc} ) = 0,$$ with the arbitrary normalization \(\sum_{i=0}^m c_i = 1\). The \(c_i\)’s can be obtained from the \(a_i\)’s and \(b\) as \((c_0,c_1,\dots,c_{m-1},c_m)\propto (a_0,a_1,\dots,a_{m-1},-1)\). We then have $$x_{\rm acc} = \sum_{i=0}^m c_{i} x_{k+i}.$$ Again, the parameters \(c_i\)’s depend on \(k\), but we omit this dependence.

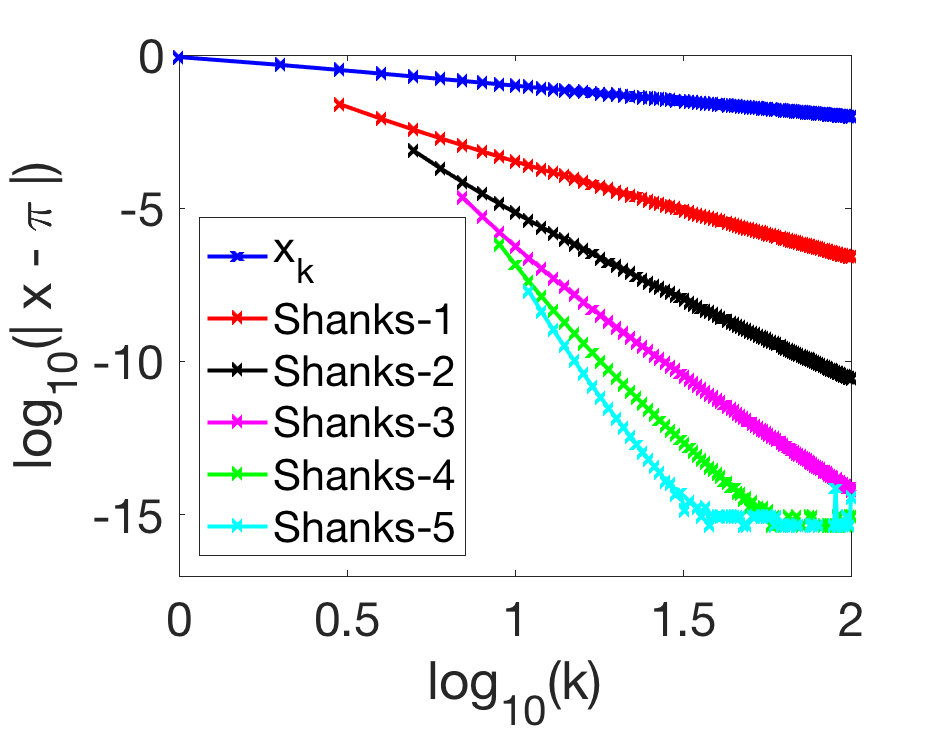
In order to estimate the \(m+1\) parameters \(c_0,\dots,c_m\), we subtract two versions of the equality for \(k\) and \(k+1\), leading to $$\sum_{i=0}^m c_i ( x_{k+1+i} – x_{k+i} ) = 0.$$ Defining the matrix \(U \in \mathbb{R}^{m \times (m+1)}\) by $$U_{ji} = x_{k+1+i+j} – x_{k+i+j},$$ for \(i \in \{0,\dots,m\}\) and \(j \in \{0,\dots,m-1\}\), we have $$ U c = 0. $$ Together with the constraint \(1_{m+1}^\top c = 1\), this leads to the correct number of equations to estimate \(c\), from \(2m+1\) iterates \(x_k,\dots,x_{k+2m}\). The extrapolated iterate \(x^{(m)}_k\) is then $$x^{(m)}_k = x_{\rm acc} = \sum_{i=0}^m c_{i} x_{k+i}.$$ Note that the extrapolation is exact when the sequence is exactly following a \(m\)-th order recursion. See an example of application on the Leibniz formula below.

Extension to vectors

We now consider accelerating vector sequences \(x_k \in \mathbb{R}^d\). There are multiple approaches to extend acceleration from real numbers to vectors, as presented in [4, 5]. The simplest way is to apply high-order extrapolation to all coordinates separately; this depends however a lot on the chosen basis, requires too many linear systems to solve, and performs worse (see examples below for gradient descent). An alternative is to consider a specific notion of inversion for vectors called Samelson inversion, which then leads to the so-called vector \(\varepsilon\)-algorithm [10]. We now present a vector extension which exists under many names: the Eddy-Mesina method [6,7], reduced rank extrapolation [4, 11, 12], or Anderson acceleration [8].

We want to model the sequence \(x_k \in \mathbb{R}^d\) as $$x_{k+1} = A x_{k} + b,$$ where \(A \in \mathbb{R}^{d \times d}\) and \(b \in \mathbb{R}^d\). By a simple variable / equation counting arguments, there are \(d^2+d\) parameters, and we thus need \(d+1\) equations in \(\mathbb{R}^d\), and thus \(d+2\) consecutive iterates, to estimate \(A\) and \(b\).

In order to use only \(m+2\) iterates, with \(m \) much less than \(d\), we will focus directly on the extrapolation equation $$x_{\rm acc} = c_0 x_k + c_1 x_{k+1}+ \cdots +c_m x_{k+m}, $$ with the constraint that \(c_0+c_1+\cdots+c_m =1\). Therefore, we will not try to explicitly fit the model parameters \(A\) and \(b\).

A sufficient condition for good extrapolation weights is that the extrapolated version is close for two consecutive \(k\)’s, that is $$c_0 x_k + c_1 x_{k+1}+ \cdots +c_m x_{k+m} \approx c_0 x_{k+1} + c_1 x_{k+2}+ \cdots +c_m x_{k+m+1},$$ which can be rewritten as $$c_0 (x_{k}-x_{k+1}) + c_1 ( x_{k+1} -x_{k+2}) + \cdots + c_m (x_{k+m} – x_{k+m+1}) \approx 0.$$ A natural criterion is thus to minimize the \(\ell_2\)-norm $$ \big\| c_0 \Delta x_{k} + c_1 \Delta x_{k+1} + \cdots + c_m \Delta x_{k+m} \big\|_2 \mbox{ such that } c_0+c_1+\cdots+c_m = 1,$$ where \(\Delta x_{i} = x_{i} -x_{i+1}\). Denoting \(U \in \mathbb{R}^{d \times (m+1)}\) the matrix with columns \(\Delta x_{k}, \dots, \Delta x_{k+m}\), we need to minimize \(\| U c \|_2\) such that \(c^\top 1_{m+1} = 1\), whose solution is $$ c \propto ( U^\top U)^{-1} 1_{m+1}, \mbox{ that is, } c = \frac{1}{1_{m+1}^\top (U^\top U)^{-1} 1_{m+1}} ( U^\top U)^{-1} 1_{m+1}.$$ Note that while the weights \(c_0,\dots,c_m\) sum to one, they may be negative, that is, the extrapolated sequence is not always a convex combination (hence the name extrapolation). Moreover, note that unless \(m\) is large enough, the optimal \(U c\) is in general not equal to zero (it is when modelling real sequences, see below).

For \(m=1\), the solution is particularly simple, as we need to minimize $$ \|\Delta x_{k+1} – c_0 ( \Delta x_{k+1} – \Delta x_k ) \|^2,$$ leading to $$c_0 = \frac{\Delta x_{k+1}^\top ( \Delta x_{k+1} – \Delta x_k )}{ \| \Delta x_{k+1} – \Delta x_k \|^2} \mbox{ and } c_1 = \frac{\Delta x_{k}^\top ( \Delta x_{k} – \Delta x_{k+1} )}{ \| \Delta x_{k+1} – \Delta x_k \|^2}.$$ The acute reader can check that when \(d=1\), we recover Aitken’s formula. See an example in two dimensions below.

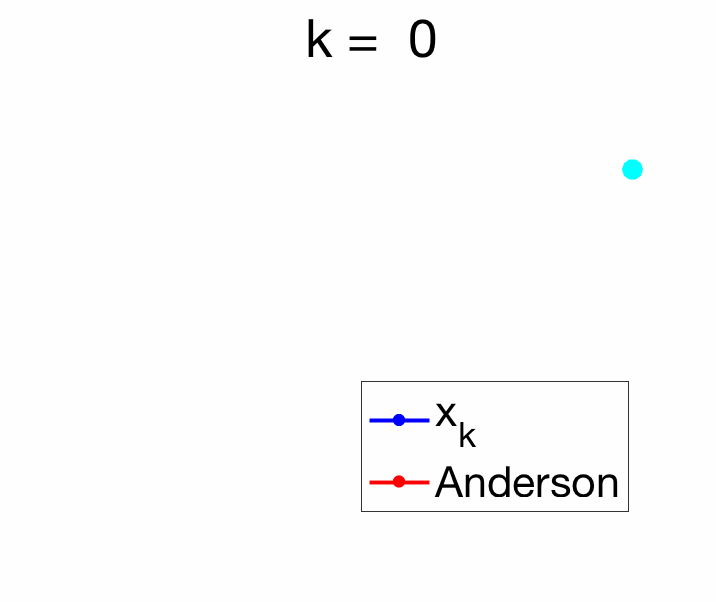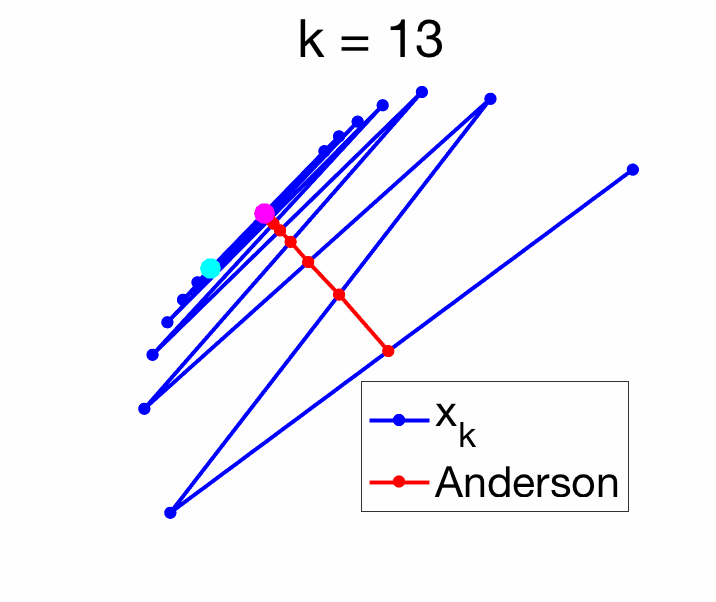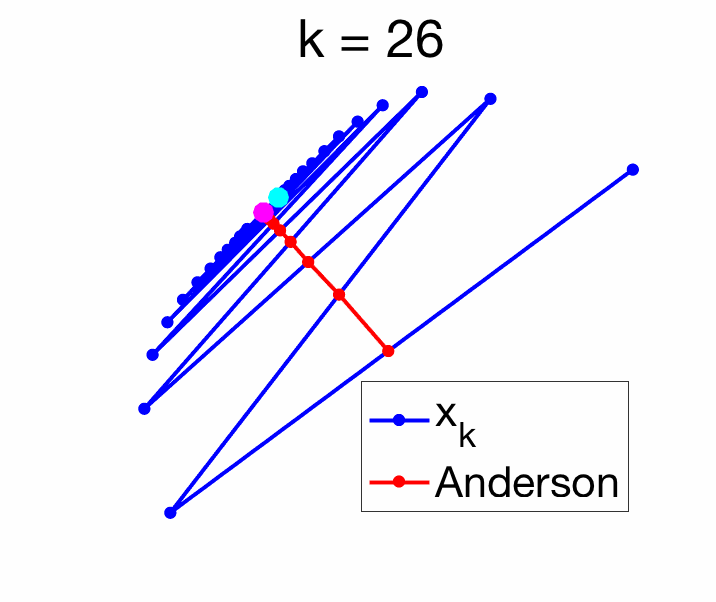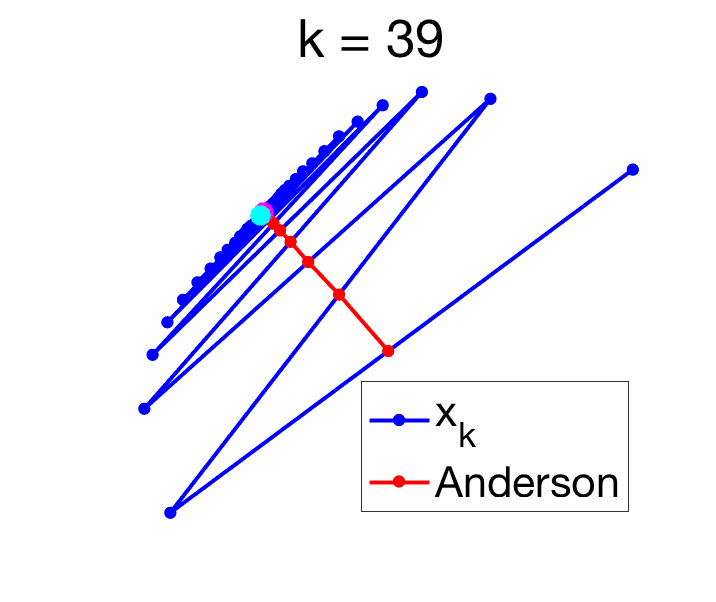
Recovering one-dimensional sequence acceleration. Given a real sequence \(y_k \in \mathbb{R}\), we can define the vector \(x_k\) in \(\mathbb{R}^m\) as $$x_k = \left( \begin{array}{c} y_k \\ y_{k+1} \\ \vdots \\ y_{k+m-1} \end{array} \right).$$ One can then check that the matrix \(U\) defined for this vector sequence is exactly the same as the matrix \(U\) defined earlier for the real valued sequence. The optimal \(\| Uc \|\) is then equal to zero (which is not the case in general).

When is it exact? The derivation I followed is only intuitive, and as for the other acceleration mechanisms, a natural question is: when is it exact? We will consider linear recursions.

Analysis for linear recursions. Assuming that \(x_{k+1} = A x_{k} + b\) is exact for all \(k \geq 0\), then \(x_k – x_\ast = A^{k} ( x_0 – x_\ast)\), and thus, following [13], $$\sum_{i=0}^m c_i (x_{k+i}-x_{k+i+1}) = \sum_{i=0}^m c_i A^{i} A^{k}(I – A )(x_0 -x_\ast) = P_m(A)(I – A) A^{k}(x_0 -x_\ast) ,$$ for \(P_m(\sigma) = \sum_{i=0}^m c_i \sigma^{i}\) a \(m\)-th order polynomial such that \(P_m(1) = 1\). We can write \(Uc\) as $$ Uc = P_m(A) ( x_k – x_{k+1}) = ( I – A) P_m(A) (x_k – x_\ast) .$$ The error between the true limit and the extrapolation is equal to: $$ x_\ast – \sum_{i=0}^m c_i x_{k+i} = \sum_{i=0}^m c_i ( x_\ast – x_{k+i} ) = P_m(A) ( x_\ast -x_{k}) = (I-A)^{-1} Uc.$$ Thus, we have $$ \Big\| x_\ast – \sum_{i=0}^m c_i x_{k+i} \Big\|_2 \leq \| U c \|_2 \times \|(I – A)^{-1}\|_{\rm op} \leq \|(I – A)^{-1}\|_{\rm op} \|I – A\|_{\rm op} \|P_m(A) ( x_k – x_\ast)\|. $$

The method will be exact when one can find a degree \(m\) polynomial so that \(P_m(A) (x_{k} – x_\ast) = 0 \), and a sufficient condition is that \(P_m(A)=0\), which is only possible if \(A\) had only \(m\) distinct eigenvalues. This is exactly minimal polynomial extrapolation [9]. Another situation is when \(m = d\) (like for the special case of real sequences above).

Otherwise, the method will be inexact, but the method can find a good polynomial \(P_m\), and the error is less than the infimum of \( \|P_m(A) ( x_k – x_\ast)\|\) over all polynomial of degree \(m\) such that \(P_m(1)=1\). Assuming that the matrix \(A\) is symmetric and with all eigenvalues between \(-\rho\) and \(\rho\) (which will be the case for the gradient method below), then the error is less than the infimum of \(\sup_{\sigma \in [-\rho,\rho]} |P_m(\sigma)|\), which is attained for the Chebyshev polynomial (see a previous post). The improvement in terms of convergence is similar to Chebyshev acceleration, but (a) without the need to know \(\rho\) in advance (the method is totally adaptive), and (b) with a provable robustness when the iterates deviate from following an autoregressive process (see [13] for details).

Going beyond linear recursions. As presented, Anderson acceleration does not lead to stable acceleration (see the experiment below for gradient descent). The main reason is that when iterates deviate from an autoregressive process, or when the recursion is naturally noisy, the estimation of the parameters \(c\) is unstable, in particular because the matrix \(U^\top U\) which has to be inverted is severely ill-conditioned [14]. In a joint work with Damien Scieur and Alexandre d’Aspremont, we considered regularizing the estimation of \(c\) by penalizing its \(\ell_2\)-norm. We thus minimize \( \| U c \|_2^2 + \lambda \| c\|_2^2\) such that \(c^\top 1_{m+1} = 1\), whose solution is $$ c \propto ( U^\top U + \lambda I)^{-1} 1_{m+1}, \mbox{ that is, } c = \frac{1}{1_{m+1}^\top (U^\top U + \lambda I)^{-1} 1_{m+1}} ( U^\top U + \lambda I)^{-1} 1_{m+1}.$$ This simple modification leads to theoretical guarantees for non-linear recursions, and I will refer to it as regularized non-linear acceleration (RNA, see [13] for details; the “non-linearity” comes from the non-linear dependence of \(c\) on the iterates).

Application to gradient descent

We can apply RNA to the recursion, $$x_{k+1} = x_k – \gamma \nabla f(x_k),$$ where \(f: \mathbb{R}^d \to \mathbb{R}^d\) is a differentiable function, and \(\gamma\) a step-size. In the plot below, we consider accelerating gradient descent with \(m\)-th order RNA, with \(m=8\). We compare this acceleration with applying RNA to each variable separately (“RNA-univ.”), and to the unregularized version (“Anderson”). We can see the benefits of our simple extrapolation steps, and in particular the instability of unregularized acceleration.

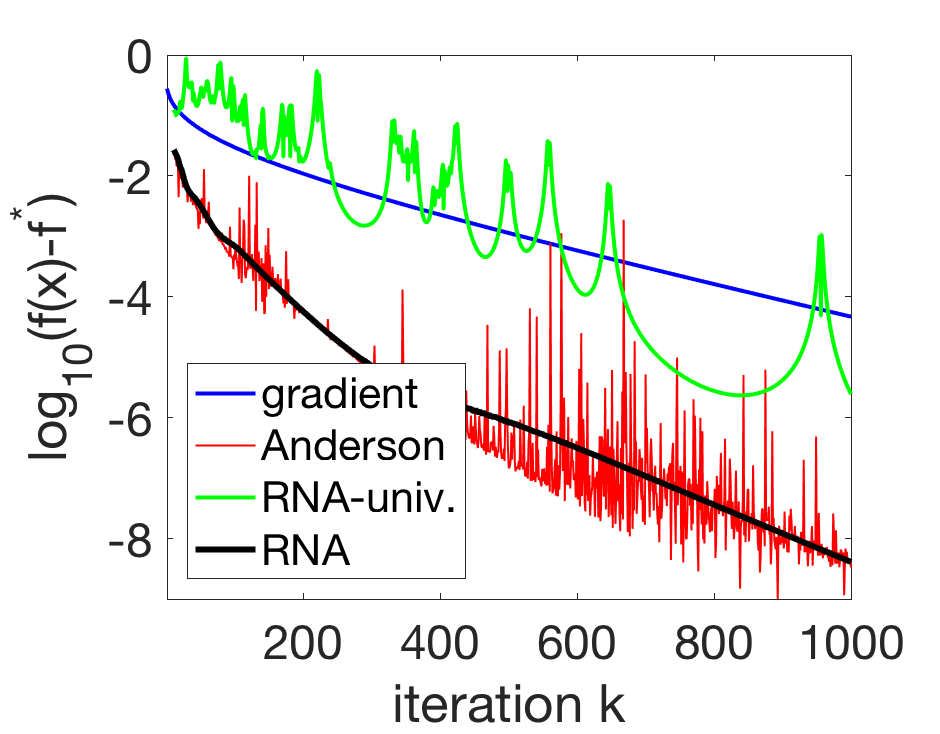
In order to obtain stronger benefits from non-linear acceleration, several extensions are considered in [13]; in particular line search to find the good regularization parameter \(\lambda\) is quite useful. Another interesting extension is the online version of the algorithm [16, section 2.5], where the extrapolated sequence is used directly within the acceleration procedure, and not as a separate sequence with no interaction with the original gradient method: this corresponds to using RNA to accelerate iterates coming from RNA!

Moreover, while the simplest theoretical guarantees come for deterministic convex optimization problems and gradient descent, RNA can be extended to stochastic algorithms [15] and to non-convex optimization problems such as the ones encountered in deep learning [16].

Conclusion

In this post, I described acceleration techniques that combine iterates of an existing algorithm, without the need to understand finely the inner structure of the original algorithm. They come at little extra-cost and can provide strong benefits.

This month’s post was dedicated to algorithms which converge linearly, that is, the iterates are asymptotically equivalent to sums of exponentials. Next month, I will consider situations where the convergence is sublinear, where Richardson extrapolation excels.

Acknowledgements. This post is based on joint work with Damien Scieur and Alexandre d’Aspremont, and in particular on their presentation slides. I would also like to thank them for proofreading this blog post and making good clarifying suggestions.

References

[1] Alexander Aitken, On Bernoulli’s numerical solution of algebraic equations, Proceedings of the Royal Society of Edinburgh, 46:289–305, 1926.
[2] Peter Wynn. On a device for computing the \(e_m(S_n)\) transformation. Mathematical Tables and Other Aids to Computation, 91-96, 1956.
[3] Claude Brezinski. Accélération de la convergence en analyse numérique. Lecture notes in mathematics, Springer (584), 1977.
[4] David A. Smith, William F. Ford, Avram Sidi. Extrapolation methods for vector sequences. SIAM review, 29(2):199-233, 1987
[5] Allan J. Macleod. Acceleration of vector sequences by multi‐dimensional \(\Delta^2\) methods. Communications in Applied Numerical Methods, 2(4):385-392, 1986.
[6] Marián Mešina. Convergence acceleration for the iterative solution of the equations X= AX+ f. Computer Methods in Applied Mechanics and Engineering, 10(2), 1977.
[7] Robert P. Eddy. Extrapolating to the limit of a vector sequence. Information linkage between applied mathematics and industry, 387-396, 1979.
[8] Homer F. Walker, Peng Ni. Anderson acceleration for fixed-point iterations. SIAM Journal on Numerical Analysis, 49(4):1715-1735, 2011.
[9] Sidi, Avram, William F. Ford, and David A. Smith. Acceleration of convergence of vector sequences. SIAM Journal on Numerical Analysis 23(1):178-196, 1986.
[10] Peter Wynn. Acceleration techniques for iterated vector and matrix problems. Mathematics of Computation, 16(79), 301-322, 1962.
[11] Stan Cabay, L. W. Jackson. A polynomial extrapolation method for finding limits and antilimits of vector sequences. SIAM Journal on Numerical Analysis, 13(5), 734-752, 1976.
[12] Stig Skelboe. Computation of the periodic steady-state response of nonlinear networks by extrapolation methods. IEEE Transactions on Circuits and Systems, 27(3), 161-175, 1980.
[13] Damien Scieur, Alexandre d’Aspremont, Francis Bach. Regularized Nonlinear Acceleration. Mathematical Programming, 2018.
[14] Evgenij E. Tyrtyshnikov. How bad are Hankel matrices? Numerische Mathematik, 67(2):261-269, 1994.
[15] Damien Scieur, Alexandre d’Aspremont, Francis Bach. Nonlinear Acceleration of Stochastic Algorithms. Advances in Neural Information Processing Systems (NIPS), 2017.
[16] Damien Scieur, Edouard Oyallon, Alexandre d’Aspremont, Francis Bach. Nonlinear Acceleration of Deep Neural Networks. Technical report, arXiv-1805.09639, 2018.
[17] Claude Brezinski and Michela Redivo-Zaglia, Extrapolation Methods: Theory and Practice, Elsevier, 2013.

Asymptotic analysis for Aitken’s \(\Delta^2\) process

In one dimension, we do not need the auto-regressive model to be exact, and an asymptotic analysis is possible. The asymptotic condition corresponds to \(\displaystyle \frac{x_{k+1}-x_\ast}{x_k – x_\ast}\) converging to a constant \(a \in [-1,1)\). More precisely if $$\frac{x_{k+1}-x_\ast}{x_k – x_\ast} = a + \varepsilon_{k+1},$$ with \(\varepsilon_k\) tending to zero, then we can estimate \(a\) through the Aitkens \(\Delta^2\) method [1] as, $$ a_{k+1} = \frac{x_{k+1}-x_k}{x_{k}-x_{k-1}} = \frac{(x_{k+1}-x_\ast) – (x_k-x_\ast) }{(x_{k} – x_\ast) -( x_{k-1}-x_\ast) } = \frac{ a + \varepsilon_{k+1} – 1}{1 – 1/(a+\varepsilon_{k})} = a + \varepsilon_{k+1} + o( \varepsilon_{k+1}).$$ A closer Taylor expansion leads to $$ a + \varepsilon_{k} + \frac{1}{a-1}( \varepsilon_{k+1}- \varepsilon_{k}) + O(\varepsilon_{k}^2).$$ We can then provide a better estimate of \(x_\ast\) as $$ \frac{x_{k+1} – a_{k+1}x_k}{1- a_{k+1}} = x_\ast + \frac{x_{k+1} -x_\ast – a_{k+1}( x_k-x_\ast)}{1- a_{k+1}} = x_\ast + \frac{(a+\varepsilon_{k+1}-a_{k+1}) ( x_k – x_\ast)}{1-a_{k+1}},$$ whose difference with \(x_\ast\) is equivalent to $$ \frac{(a+\varepsilon_k-a_{k+1}) ( x_k – x_\ast)}{1-a } \sim \frac{\varepsilon_{k+1}- \varepsilon_{k}}{(1-a)^2} ( x_k – x_\ast).$$ We have thus provided an acceleration of order \(\displaystyle \frac{\varepsilon_{k+1}- \varepsilon_{k}}{(1-a)^2} \).

High-order Shanks transformation

In order to relate our formulas to classical expressions, we first rewrite the recursion for \(m=1\) and then \(m=2\), and then to general \(m\).

First-order recursion (Aitken’s \(\Delta^2\)). We write the autorecursive recursion as $$ (x_{k+1} – x_\ast) = a ( x_{k} – x_\ast) \Leftrightarrow c_0(x_k – x_\ast) + c_1 (x_{k+1}-x_\ast) = 0 ,$$ with the constraint \(c_0 + c_1 = 1\), that is, \(c_0 = \frac{-a}{1-a}\) and \(c_1 = \frac{1}{1-a}\). We can then write \(x_\ast = c_0 x_k + c_1 x_{k+1}\), and we have the linear system in \((c_0,c_1,x_\ast)\): $$ \left( \begin{array}{ccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & 0 \\ 1 & 1 & 0 \\ x_k & x_{k+1} & – 1 \end{array}\right) \left( \begin{array}{c} c_0 \\ c_1 \\ x_\ast \end{array}\right) = \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right), $$ which can be solved using Cramer’s formula $$x_{\rm acc} = x_\ast = \frac{\left| \begin{array}{cc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} \\ x_{k} & x_{k+1} \end{array}\right|}{\left| \begin{array}{cc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} \\ 1 & 1 \end{array}\right|},$$ which leads to the same formula for \(x^{(1)}_k\).

Second-order recursion. Here, we only consider the case \(m=2\) for simplicity. We consider the model, $$c_0 (x_k – x_\ast) + c_1 (x_{k+1} – x_\ast)+ c_{2} (x_{k+2} – x_\ast) = 0, $$ with the normalization \(c_0 + c_1 + c_2 = 1\). We can then extract \(x_\ast\) as $$ x_\ast = c_0 x_k + c_1 x_{k+1} + c_2 x_{k+2}.$$ In order to provide the extra \(2\) equations that are necessary to estimate the three parameters, we take first order differences and get $$c_0 (x_k -x_{k+1}) + c_1 (x_{k+1}-x_{k+2}) + c_2 ( x_{k+2} – x_{k+3} ) =0,$$ for \(k\) and \(k+1\). This leads to the linear system in \((c_0,c_1, c_2, x_\ast)\): $$ \left( \begin{array}{cccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & x_{k+2} – x_{k+3} & 0 \\ x_{k+1}-x_{k+2} & x_{k+2}-x_{k+3} & x_{k+3} – x_{k+4} & 0 \\ 1 & 1 & 1 & 0 \\ x_{k} & x_{k+1} & x_{k+2} & – 1 \end{array}\right) \left( \begin{array}{c} c_0 \\ c_1 \\ c_2 \\ x_\ast \end{array}\right) = \left( \begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right), $$ which can be solved using Cramer’s rule (and classical manipulations of determinants) as $$x_k^{(2)} = \frac{\left| \begin{array}{ccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & x_{k+2} – x_{k+3} \\ x_{k+1}-x_{k+2} & x_{k+2}-x_{k+3} & x_{k+3} – x_{k+4} \\ x_{k} & x_{k+1} & x_{k+2} \end{array} \right|}{\left| \begin{array}{ccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & x_{k+2} – x_{k+3} \\ x_{k+1}-x_{k+2} & x_{k+2}-x_{k+3} & x_{k+3} – x_{k+4} \\ 1 & 1 & 1 & \end{array} \right|}.$$

The formula extends to order \(m\) (see below) and is often called the Shanks transformation; it is cumbersome and not easy to use. However, the coefficients can be computed recursively (which is to be expected for a Hankel matrix, but rather tricky to derive), through Wynn’s \(\varepsilon\)-algorithm. See [3] for a survey on acceleration and extrapolation.

Higher-order recursion. We consider the model, for \(m \geq 1\), $$c_0 (x_k – x_\ast) + c_1 (x_{k+1} – x_\ast) + \cdots + c_{m} (x_{k+m} – x_\ast) = 0, $$ with the normalization \(c_0 + c_1 + \cdots + c_m = 1\). We can then extract \(x_\ast\) as $$ x_\ast = c_0 x_k + c_1 x_{k+1} + \cdots + c_m x_{k+m}.$$ In order to provide the extra \(m\) equations, we take first order differences and get $$c_0 (x_k -x_{k+1}) + c_1 (x_{k+1}-x_{k+2}) + \cdots + c_m ( x_{k+m} – x_{k+m+1} ) =0,$$ for \(k, k+1,\dots, k+m-1\). This leads to the linear system in \((c_0,c_1,\cdots, c_m, x_\ast)\): $$ \left( \begin{array}{ccccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & \cdots & x_{k+m} – x_{k+m+1} & 0 \\ x_{k+1}-x_{k+2} & x_{k+2}-x_{k+3} & \cdots & x_{k+m+1} – x_{k+m+2} & 0 \\ \vdots & \vdots & & \vdots & \vdots \\ x_{k+m-1}-x_{k+m} & x_{k+m}-x_{k+m+1} & \cdots & x_{k+2m-1} – x_{k+2m} & 0 \\ 1 & 1 & \dots & 1 & 0 \\ x_{k+m} & x_{k+m+1} & \cdots & x_{k+2m} & – 1 \end{array}\right) \left( \begin{array}{c} c_0 \\ c_1 \\ \vdots \\ c_m \\ x_\ast \end{array}\right) = \left( \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \\ 0 \end{array}\right), $$ which can be solved using Cramer’s formula $$x_\ast = \frac{\left|\begin{array}{cccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & \cdots & x_{k+m} – x_{k+m+1} \\ x_{k+1}-x_{k+2} & x_{k+2}-x_{k+3} & \cdots & x_{k+m+1} – x_{k+m+2} \\ \vdots & \vdots & & \vdots \\ x_{k+m-1}-x_{k+m} & x_{k+m}-x_{k+m+1} & \cdots & x_{k+2m-1} – x_{k+2m} \\ x_{k+m} & x_{k+m+1} & \cdots & x_{k+2m} \end{array} \right|}{\left|\begin{array}{cccc} x_{k}-x_{k+1} & x_{k+1}-x_{k+2} & \cdots & x_{k+m} – x_{k+m+1} \\ x_{k+1}-x_{k+2} & x_{k+2}-x_{k+3} & \cdots & x_{k+m+1} – x_{k+m+2} \\ \vdots & \vdots & & \vdots \\ x_{k+m-1}-x_{k+m} & x_{k+m}-x_{k+m+1} & \cdots & x_{k+2m-1} – x_{k+2m} \\ 1 & 1 & \cdots & 1 \end{array} \right|}.$$

Like for \(m=1\), Wynn’s \(\varepsilon\)-algorithm can be used to compute the iterates recursively.