Finding global minima with kernel approximations

Last month, I showed how global optimization based only on accessing function values can be hard with no convexity assumption. In a nutshell, with limited smoothness, the number of function evaluations has to grow exponentially fast in dimension, which is a rather negative statement. On the positive side, this number does not grow as fast for highly smooth functions. However, optimal algorithms end up approximating the whole function to minimize, and then minimizing the approximation, which takes exponential time in general. In this post, I will describe very recent work with Alessandro Rudi and Ulysse Marteau-Ferey [1] that essentially jointly approximates the function and minimizes the approximation.

Our task for this post will be to minimize a function \(f: \mathbb{R}^d \to \mathbb{R}\), for which we know the global minimizer is already located in a certain bounded set \(\Omega\) (typically a large ball). We can query values of \(f\) at any point in \(\Omega\).

It turns out it can be formulated as a convex optimization problem (there has to be a catch in this statement, stay tuned).

All optimization problems are convex!

We consider the following minimization problem: $$\tag{1} \sup_{c \in \mathbb{R}} \ c \ \ \mbox{ such that } \ \ \forall x \in \Omega, \ f(x) \geqslant c.$$ As illustrated below, this corresponds to finding the largest lower bound \(c\) on the function.

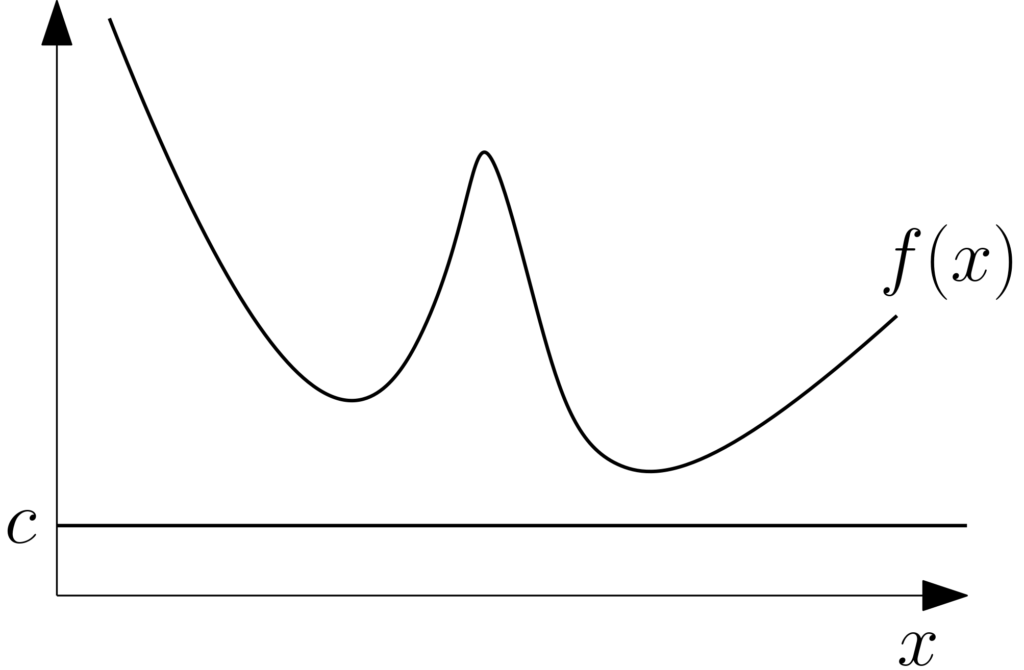
Assuming \(f\) attains its global minimizer \(f_\ast\) in \(\Omega\), then the optimal value of the problem above is attained and is clearly \(f_\ast\), that is, the problem in Eq. (1) leads to the minimal value of \(f\).

Moreover, each constraint in Eq. (1) is a linear constraint in \(c\), and the objective is linear. Hence we obtain a linear programming problem which is a particularly simple instance of a convex optimization problem. Thus, all optimization problems are convex!

The catch here is that the set of inequalities is dense, that is, in general, \(\Omega\) contains infinitely many elements, and thus the number of constraints is infinite.

Duality. It is worth deriving the convex optimization dual (being loose here in terms of regularity and integrability conditions). We add a Lagrange multiplier \(\mu(x) \geqslant 0\) for each of the constraints \(f(x) \, – c \geqslant 0\), and consider the Lagrangian
$$ \mathcal{L}(c,\mu) = c + \int_{\Omega} \! \mu(x) \big( f(x) \, – c\big) dx.$$ Maximizing it with respect to \(c\) leads to the constraint \(\int_\Omega \mu(x) dx = 1\), that is, \(\mu\) represents a probability distribution, and the dual problem is $$ \inf_{\mu \in \mathbb{R}^\Omega} \int_{\Omega} \! \mu(x) f(x) dx \ \ \mbox{ such that } \int_\Omega\! \mu(x) dx = 1 \mbox{ and } \forall x \in \Omega, \ \mu(x) \geqslant 0.$$ In words, we minimize the expectation of \(f\) with respect to all probability distributions on \(\Omega\) with densities. Here, the infimum is obtained from any probability measure that puts mass only on the minimizer of \(f\) on \(\Omega\). This measure is typically not absolutely continuous, and thus the infimum is not attained (no big deal).

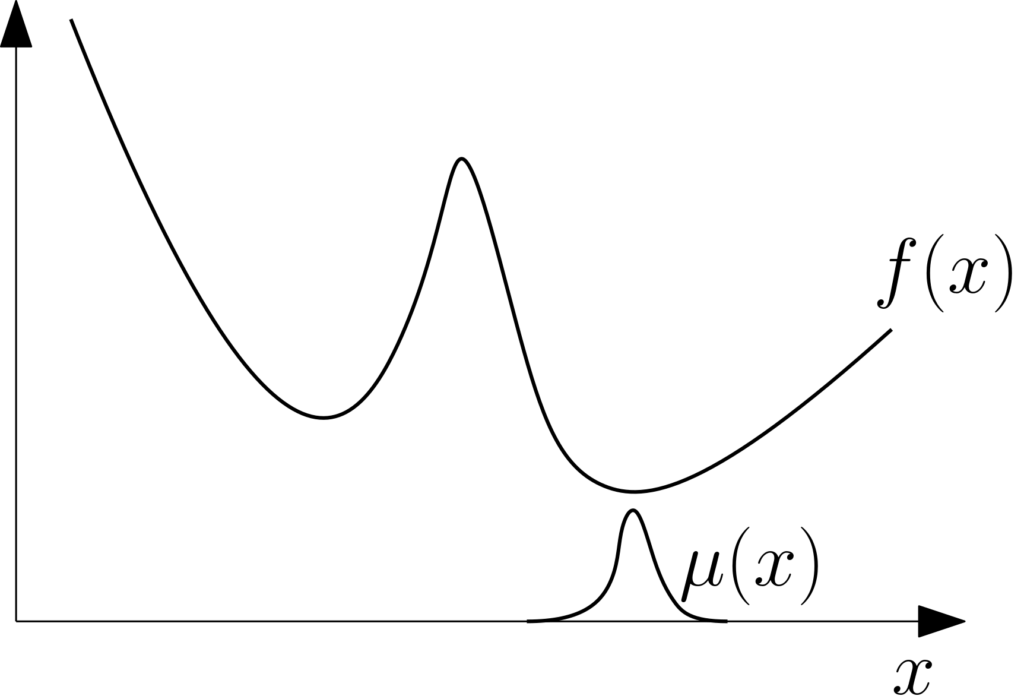
This is also a convex optimization problem, with a linear objective function on the infinite-dimensional set of probability measures.

Overall, we get convex but (apparently) useless problems. We will first need an efficient way to represent non-negativity of functions (this will be applied to \(f(x) \, – c\)).

Positivity with “sums of squares”

We now start to make some assumptions on the function \(f\) to be minimized. We will assume that it can be written as $$\forall x \in \Omega, \ f(x) = \langle \phi(x), F \phi(x) \rangle,$$ for some feature vector \(\phi(x)\) in some Hilbert space \(\mathcal{H}\), and \(F\) a symmetric linear operator on \(\mathcal{H}\).

We will need infinite dimensions later, but you can safely assume that \(\mathcal{H}\) is a classical Euclidean space (e.g., \(\mathbb{R}^{{\rm dim}(\mathcal{H})}\)), and that we have $$\forall x \in \Omega, \ f(x) = \phi(x)^\top F \phi(x) = \sum_{i,j=1}^{{\rm dim}(\mathcal{H})} F_{ij} \phi(x)_i \phi(x)_j.$$

We will also assume that the constant function on \(\Omega\) can be represented as well, that is, there exists \(u \in \mathcal{H}\) such that \(\forall x \in \Omega, \ \langle u, \phi(x) \rangle = 1.\) This is to ensure that we can represent within the optimization problem above the function \(f(x) \, – c = \langle \phi(x), (F – c \, u \otimes u) \phi(x) \rangle\).

The most classical example is the set of polynomials of degree \(2r\) for which we can choose \(\phi(x)\) to be of dimension \(d+r \choose r\) and contain all monomials are degree less than \(r\). We will go infinite-dimensional and link this to kernels later in this post.

You may wonder why we are not simply modeling the function \(f\) with a classical formulation \(f(x) = \langle w, \phi(x) \rangle\). This is precisely to be able to enforce positivity.

Positivity through “sum-of-squares”. We can assume that the operator \(F\) is positive-semidefinite (which we will denote \(F \succcurlyeq 0\)), that is, all of its eigenvalues are non-negative, or, for all \(h \in \mathcal{H}\), \(\langle h, F h \rangle \geqslant 0\). Then this implies that the function \(f\) is pointwise positive. Thus: $$ \tag{2} F \succcurlyeq 0 \ \ \Rightarrow \ \ \forall x \in \Omega, \ f(x) = \langle \phi(x), F \phi(x) \rangle \geqslant 0. $$

We refer to such functions as “sum-of-squares”. Indeed, given the spectral decomposition of \(F\) as $$ F = \sum_{i \in I} \lambda_i h_i \otimes h_i, $$ with \(I\) a countable set, and \((h_i)_{i \in I}\) an orthonormal family in \(\mathcal{H}\), we have \(\lambda_i \geqslant 0\) for all \(i \in I\), and thus we can write $$ f(x) = \langle \phi(x), F \phi(x) \rangle = \sum_{i \in I} \lambda_i \langle \phi(x) , (h_i \otimes h_i) \phi(x) \rangle = \sum_{i=1}^n \big( \sqrt{\lambda_i} \langle h_i , \phi(x) \rangle \big)^2.$$ That is, the function \(f\) is a sum of squares of functions.

A key question is whether the implication in Eq. \((2)\) can be reversed. In other words, can we write all non-negative functions as sum-of-squares? The answer will depend on the chosen feature map \(\phi: \Omega \to \mathcal{H}\).

Polynomials. For polynomials, the answer is known to be positive in dimension 1, but negative in higher dimensions (see the nice review in [2]): that is, unless \(d=1\), or \(d=2\) and \(r=2\), there are polynomials of degree \(2r\) in dimension \(d\) that are non-negative but are not the sum of squares of polynomials.

Keeping in mind the difference being non-negative and being a sum of squares, let’s look how this can be used for global optimization of polynomials.

Polynomial optimization with sums-of-squares

We now consider that \(f\) is a polynomial of degree \(2r\), and that \(\phi(x)\) is of dimension \(d+r \choose r\) and contain all monomials of degree less than \(r\). We consider representing the constraint \(f(x)\geqslant c\) in Eq. (1), as \(f(x) = c + \langle \phi(x), A \phi(x) \rangle\) for some positive-definite operator (here a matrix) \(A\). With the notations above, this is equivalent to \(F = c u \otimes u + A\) and \(A \succcurlyeq 0\). This leads to the following optimization problem (no localization set \(\Omega\) is used): $$ \tag{3} \max_{c \in \mathbb{R}, A \succcurlyeq 0} c \ \mbox{ such that } \ \forall x \in \mathbb{R}^d, \ f(x) = c + \langle \phi(x), A \phi(x) \rangle .$$ This in now a problem in finite dimension, which is a semidefinite programming problem, and can thus a priori be solved in polynomial time in \(d+r \choose r\). See [3, 4] for more details.

At this point, beyond the potentially large dimension of the convex problem when \(r\) and \(d\) grow, there is a major concern: is the problem in Eq. (3) equivalent to the one in Eq. (1)? This is true if and only if the polynomial \(f(x) \, – f_\ast\) is a a sum-of-squares, which given the discussion above may not happen as soon as \(d \geqslant 2\).

In order to apply to all polynomials, the problem has to be changed. A simple reformulation is possible [3] by assuming that the global minimum of \(f\) is attained within the set \(\Omega = \{ x \in \mathbb{R}^d, \ x^\top x \leqslant R^2\}\) for some \(R > 0\). It turns out (and this is a highly non-trivial fact) that all polynomials \(f(x) \) which are positive on \(\Omega\) can be written as \(f(x) = q(x) + ( R^2 – x^\top x ) p(x)\), where \(q(x)\) and \(p(x) \) are sum-of-squares polynomials. The only issue is that the degrees of \(p\) and \(q\) are not known in advance so a sequence (a so-called “hierarchy”) of problems have to be solved with increasing degrees, each providing a lower bound on \(f_\ast\).

When the degree is large enough so that the sum-of-squares representation exists for \(f – f_\ast\), then the following problem $$ \max_{c \in \mathbb{R}, A, B \succcurlyeq 0} c \mbox{ such that } \forall x \in \mathbb{R}^d, \ f(x) = c + \langle \phi(x), A \phi(x) \rangle + ( R^2 – x^\top x ) \langle \phi(x), B \phi(x) \rangle$$ is a semi-definite program, whose solution leads to \(c = f_\ast\).

This remains a large semi-definite program whose order is not known in advance and for which complicated solvers are needed. I will now present our recent work where we go infinite-dimensional, and some of these issues are alleviated (but some others are created).

Going infinite-dimensional

We now consider \(\phi(x)\) to be infinite-dimensional. In order to allow finite-dimensional manipulations of various objects, we consider feature maps which are obtained from positive-definite kernels. More precisely, we consider the so-called Sobolev space \(\mathcal{H}\) of functions on \(\Omega\) with all partial derivatives up to order \(s\) which are square-integrable. When \(s > d/2\), then this is a reproducing kernel Hilbert space, that is, there exists a positive-definite kernel \(k: \Omega \times \Omega \to \mathbb{R}\) such that the feature map \(\phi(x) = k(\cdot,x)\) allows to access function values as \(h(x) = \langle h, \phi(x) \rangle\) for all \(h \in \mathcal{H}\). For the algorithm, we will only need access to the kernel; for example, for \(s = d/2+1/2\), we can choose the usual exponential \(k(x,y) = \exp( – \alpha \| x – y \|_2)\).

We now consider the same problem as for polynomials, but with this new feature map: $$\tag{4} \max_{c \in \mathbb{R}, A \succcurlyeq 0} c \ \mbox{ such that } \ \forall x \in \Omega, \ f(x) = c + \langle \phi(x), A \phi(x) \rangle .$$ In order to have an exact reformulation, we need that there exists some \(A_\ast\) such that \(\forall x \in \Omega, \ f(x) \, – f_\ast = \langle \phi(x), A_\ast \phi(x) \rangle\). It turns out to be true [1] with appropriate geometric conditions on \(x\) (such as isolated second-order strict global minimizers within \(\Omega\)) and regularity (at least \(s+3\) derivatives); see [1] for details.

This is all very nice, but the problem in Eq. (4) is still an infinite-dimensional problem (note that we have gone from a continuum of inequalities to elements of a Hilbert space, but that’s not much of a gain).

Controlled approximation through sampling

We can now leverage classical and more recent techniques from kernel methods. The main idea is to subsample the set of equalities in Eq. (4), that is consider \(n\) points \(x_1,\dots,x_n \in \Omega\), and solve instead the regularized sampled problem $$\tag{5} \max_{c \in \mathbb{R}, A \succcurlyeq 0} c \ – \, \lambda \, {\rm tr}(A) \ \mbox{ such that }\ \forall i \in \{1,\dots,n\}, \ f(x_i) = c + \langle \phi(x_i), A \phi(x_i) \rangle , $$ where \(\lambda > 0\) is a regularization parameter.

Approximation guarantees. Beyond computational considerations, how big does \(n\) need to be to obtain a value of \(c\) which is at most \(\varepsilon\) away from \(f_\ast\)? From last post, if \(f\) is \(m\)-times differentiable, we cannot have \(n\) smaller than \(\varepsilon^{-d/m}\). As shown in [1], for points \(x_1,\dots,x_n \in \Omega\) selected uniformly at random, then \(n\) can be taken to of the order \(\varepsilon^{-d/(m – d/2 – 3)}\) for a well-chosen Sobolev space \(s\) and regularization parameter \(\lambda\). This is not the optimal rate \(\varepsilon^{-d/(m – d/2)}\) , but close when \(m\) and \(d\) are large.

Finite-dimensional algorithm. The problem in Eq. (5) is still infinite-dimensional. We can leverage a recent work, again with Ulysse Marteau-Ferey and Alessandro Rudi [5], that shows that a representer theorem exists for this type of problems: the optimization for the operator \(A\) may be restricted to \(A\) of the form $$A = \sum_{i,j} C_{ij} \phi(x_i) \otimes \phi(x_j)$$ for a positive definite matrix \(C \in \mathbb{R}^{n \times n}\). This leads to a semi-definite programming problem of size \(n\), whose running-time complexity is polynomial in \(n\) (e.g, \(O(n^{3.5})\)), with standard general-purpose toolboxes (such as CVX).

In order to tackle large values \(n\) which are larger than \(1000\), simple iterative algorithms can be designed (see [1] for a damped Newton algorithm which does not require any singular value decompositions, with complexity \(O(n^3)\) per iteration). Classical tools for efficient kernel methods, such as column sampling / Nyström method (see [6, 7] and references therein) or random features (see [8, 9] and references therein), could also be used to avoid a cubic or quadratic complexity in \(n\).

Comparison with random search. Instead of solving the problem in Eq. (5), we could output the minimal value of \(f(x_i)\) for \(i \in \{1,\dots,n\}\), which is exactly random search if the points \(x_i\) are random (this also happens to correspond to using \(\lambda=0\) in Eq. (5)). This can only achieve an error \(\varepsilon\) for \(n\) of order \(\varepsilon^{-d}\); in other words, it cannot leverage smoothness, while our algorithm can. The main technical reason is that subsampling inequalities provide weaker guarantees than subsampling equalities, and thus representing the non-negativity of a function through an equality (which our method essentially does) provides significant benefits.

Duality

As always in convex optimization, it is beneficial to look at dual problems. It turns out that iterative algorithms are easier to build for the finite-dimensional dual problem to Eq. (5). We rather look now at the dual of Eq. (4) and make the parallel with the primal original problem in Eq. (1) and its dual.

Introducing a Lagrange multiplier \(\mu(x)\) for the constraint \(f(x) = c + \langle \phi(x), A \phi(x) \rangle\) (this time not constrained to be non-negative because we have an equality constraint), we can form the Lagrangian $$\mathcal{L}(c,A,\mu) = c + \int_{\Omega} \! \mu(x) \big( f(x) \, – c \, – \langle \phi(x), A \phi(x) \rangle \big) dx.$$ Maximizing with respect to \(c\) again leads to the constraint \(\int_\Omega \mu(x) dx = 1\), while minimizing with respect to \(A \succcurlyeq 0\) leads to the constraint \(\int_\Omega \mu(x) \phi(x) \otimes \phi(x) dx \succcurlyeq 0 .\) The dual problem thus becomes $$ \inf_{\mu \in \mathbb{R}^\Omega} \int_{\Omega} \! \mu(x) f(x) dx \ \ \mbox{ such that } \int_\Omega\! \mu(x) dx = 1 \mbox{ and } \ \int_\Omega \mu(x) \phi(x) \otimes \phi(x)dx \succcurlyeq 0.$$ The impact of the representation of non-negative functions by quadratic forms in \(\phi(x)\) is to replace the non-negativity contraint on all \(\mu(x)\) by the positivity of the matrix \(\int_\Omega \mu(x) \phi(x) \otimes \phi(x)dx\), which is weaker in general, but equivalent if \(\phi(x)\) is “large” enough.

Note that the dual problem through a signed measure that should concentrate around the minimizers of \(f\) leads to a natural candidate \(\int_\Omega x \mu(x) dx\) for the optimizer (see more details in [1], and a similar dual formulation for polynomials in [10]).

Simulations

In order to highlight how the optimization method works, I will first present how it minimizes the multi-modal function in dimension \(d=2\) pictured below on \([-1,1]^2\).

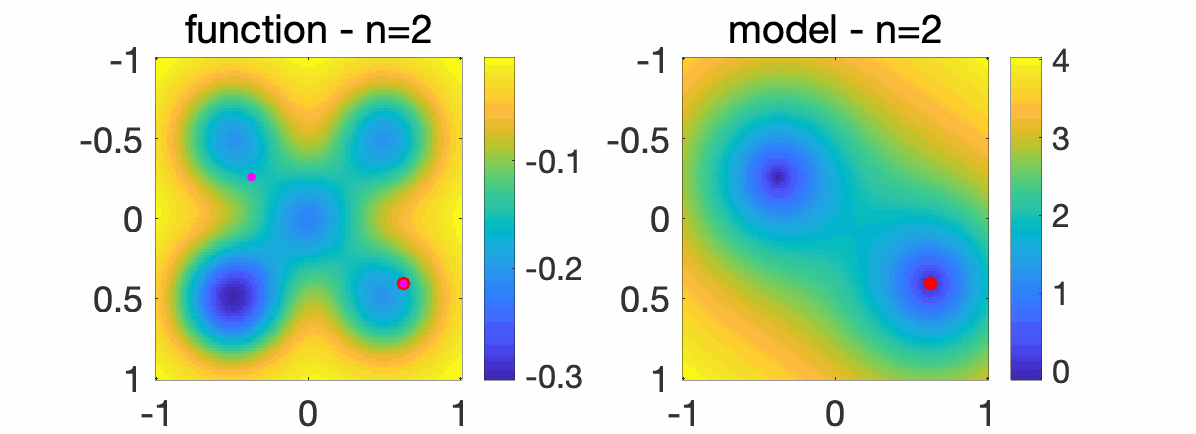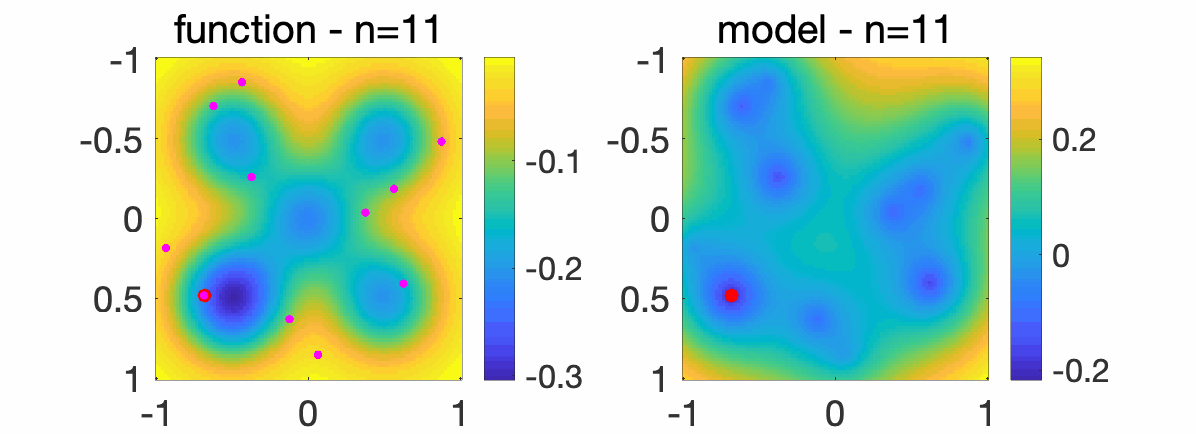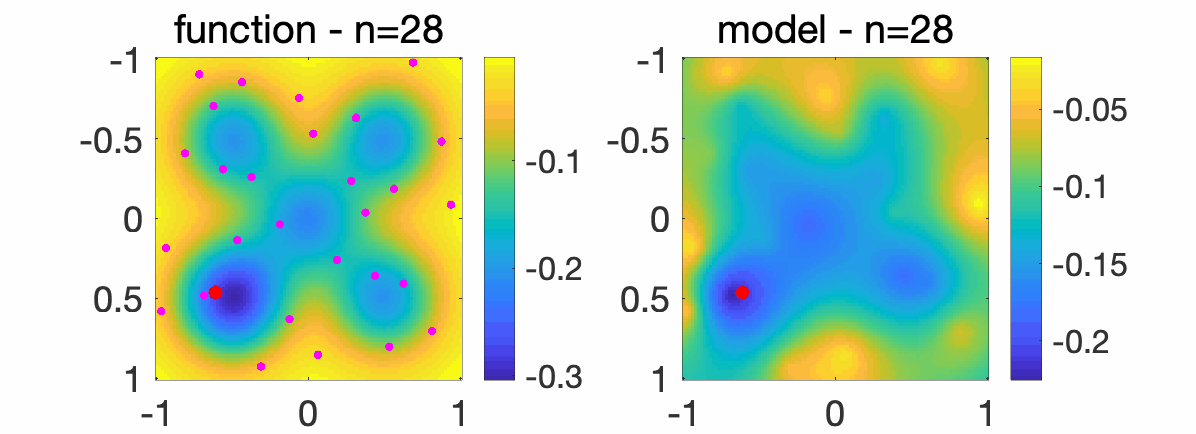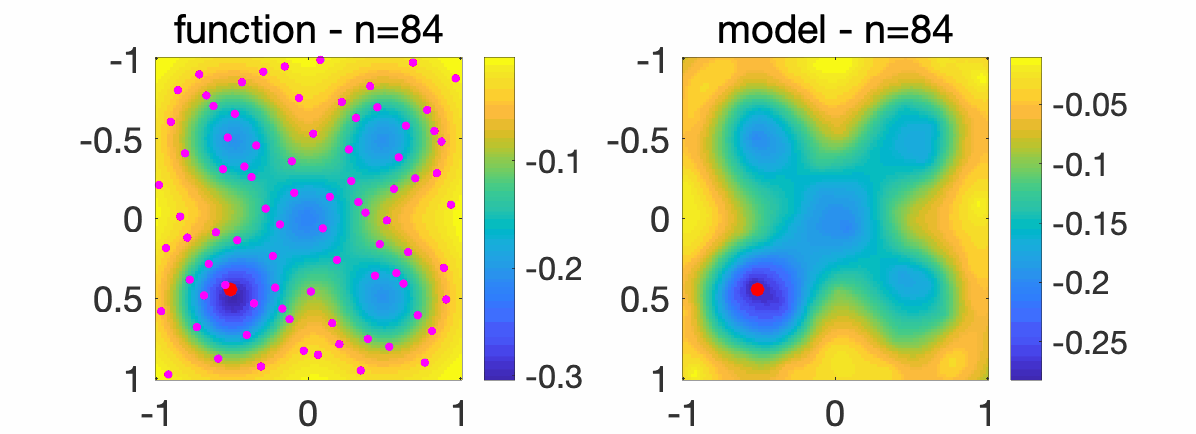
We consider sampling a sequence of points \(x_1, x_2,\dots \in \mathbb{R}^2\) from a quasi-random sequence (so that it fills the space more evenly that purely random). The random points are displayed in purple while the solution of our algorithm is displayed in red, with increasing numbers \(n\) of sampled points. On the right plot, the model \(c + \langle \phi(x), A \phi(x) \rangle\) is displayed, showing that the model becomes more accurate as \(n\) grows.

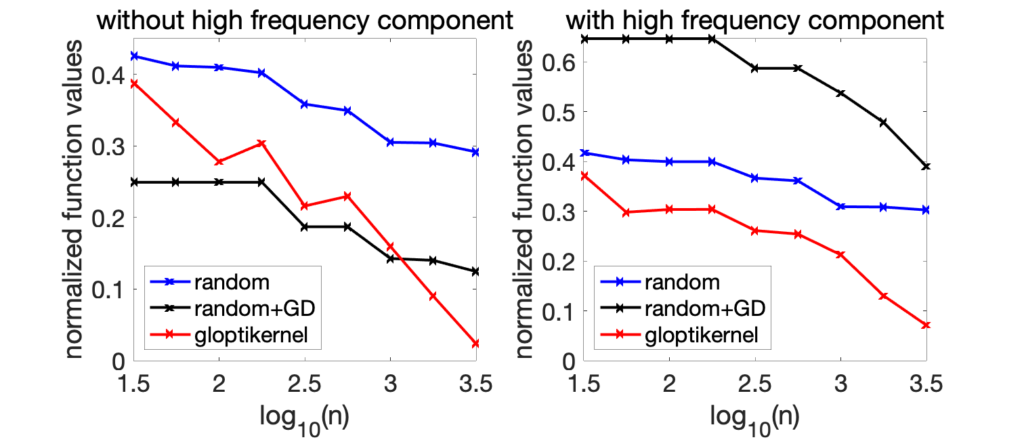
We also consider a problem in dimension \(d=8\), where we compare random sampling and our algorithm (“gloptikernel”), as \(n\) grows (see [1] for the experimental set-up).

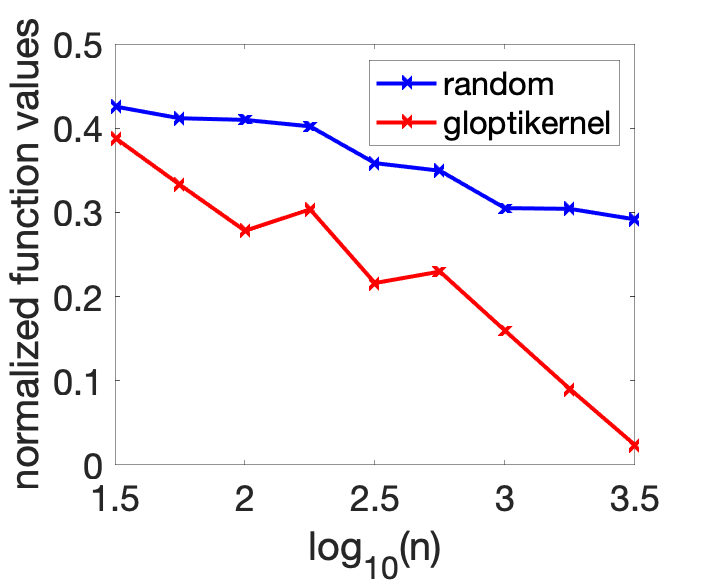
Clearly, the chosen baseline (random sampling) is rudimentary, though optimal up to logarithmic terms for non-smooth problems where only Lipschitz-continuity is assumed. We can also compare to gradient descent with random restarts (“random+GD” below, with the same overall number of function evaluations). As shown below, when the gradient information is robust, this baseline performs similarly (left plot), while when a high frequency component is added to the function (which makes the gradient information non reliable, right plot), the local descent algorithm needs more function evaluations.

It would be interesting to compare this new algorithms to other global optimization algorithms based on function evaluations, such as CMA-ES or Bayesian optimization.

Conclusion

In this post, I presented an algorithm for global optimization that can provably leverage smoothness with an algorithm which has a running time which is polynomial in the dimension and the number of function evaluations. For large smoothness factors, the number of such evaluations has a dependence on the precision \(\varepsilon\) which has no exponential dependence in dimension in the exponent (but still in the constants: we cannot optimize multivariate polynomials in polynomial time…).

These ideas can be extended in a number of ways.

General relaxation tool for dense inequalities. We can generalize the previous developments to all problems with a continuum of constraints on a variable \(\theta\), such as, $$ \forall x \in \Omega, \ H(\theta,x) \geqslant 0.$$ The corresponding Lagrange multipliers also satisfy $$ \forall x \in \Omega, \ \mu(x) \geqslant 0$$ (there may be other ones like in the problem above). Now the question is: should we use the non-negative modelisation with quadratic forms in the primal or in the dual? Or equivalently, replace the non-negativity constraint by the positivity of the integral of \(\phi(x) \otimes \phi(x)\) in the dual or in the primal?

The answer depends on the expected smoothness of the function which is non-negative. In the optimization problem, we expect \(f(x) \, – c\) to be smooth at the optimum, while \(\mu(x)\) which is approximating a Dirac clearly isn’t; therefore, the choice is clear (at least in retrospect since we originally tried to model \(\mu(x)\) as a quadratic form…).

Constrained optimization. Following [3], we can apply the same algorithmic technique to constrained optimization, by formulating the problem of minimizing \(f(x)\) such that \(g(x) > 0\) as maximizing \(c\) such that \(f(x) = c + p(x) + g(x)q(x)\), and \(p, q\) non-negative functions. We can (at least in principle) then replace the non-negative constraints by \(p(x) = \langle \phi(x),A\phi(x)\rangle\) and \(q(x) =\langle \phi(x),B\phi(x)\rangle\) for positive operators \(A\) and \(B\). All this remains to be explored in more details.

Acknowledgements. I would like to thank Alessandro Rudi and Ulysse Marteau-Ferey for proofreading this blog post and making good clarifying suggestions.

References

[1] Alessandro Rudi, Ulysse Marteau-Ferey, Francis Bach. Finding Global Minima via Kernel Approximations. Technical report arXiv:2012.11978, 2020.
[2] Walter Rudin. Sums of squares of polynomials. The American Mathematical Monthly, 107(9), 813-821, 2000.
[3] Jean-Bernard Lasserre. Global optimization with polynomials and the problem of moments. SIAM Journal on Optimization, 11(3):796–817, 2001.
[4] Jean-Bernard Lasserre. Moments, Positive Polynomials and their Applications, volume 1. World Scientific, 2010.
[5] Ulysse Marteau-Ferey, Francis Bach, and Alessandro Rudi. Non-parametric models for non-negative functions. Advances in Neural Information Processing Systems, 33, 2020.
[6] Francis Bach. Sharp analysis of low-rank kernel matrix approximations. Conference on Learning Theory, pages 185–209, 2013.
[7] Alessandro Rudi, Raffaello Camoriano, and Lorenzo Rosasco. Less is more: Nyström computational regularization. Advances in Neural Information Processing Systems, 2015.
[8] Alessandro Rudi and Lorenzo Rosasco. Generalization properties of learning with random features. Advances in Neural Information Processing Systems, 30, 2017.
[9] Francis Bach. On the equivalence between kernel quadrature rules and random feature expansions. Journal of Machine Learning Research, 18(1):714–751, 2017.
[10] Jean-Bernard Lasserre. The moment-SOS hierarchy and the Christoffel-Darboux kernel. Technical Report arXiv:2011.08566, 2020.