Revisiting the classics: Jensen’s inequality

There are a few mathematical results that any researcher in applied mathematics uses on a daily basis. One of them is Jensen’s inequality, which allows bounding expectations of functions of random variables. This really happens a lot in any probabilistic arguments but also as a tool to generate inequalities and optimization algorithms. In this blog post, I will present a collection of fun facts about the inequality, from very classical to more obscure. If you know other cool ones, please add them as comments.

But before, let me be very clear: Jensen’s inequality is often not in the direction that you would hope it to be. So, to avoid embarrassing mistakes, I always draw at least in my mind the figure below before using it.

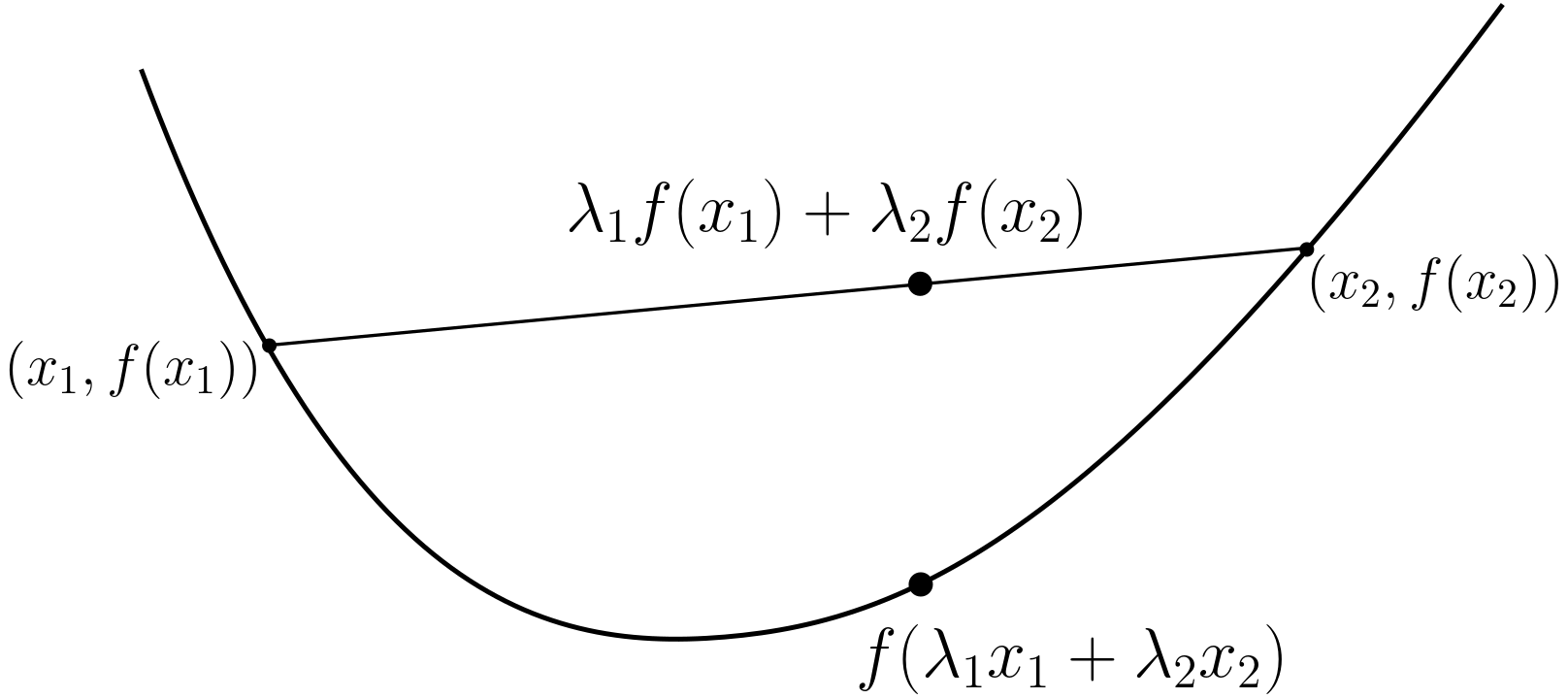
Simplest formulation and proof

Given a convex function defined on a convex subset \(C\) of \(\mathbb{R}^d\), and a random vector \(X\) with values in \(C\), then $$ f\big( \mathbb{E}[X] \big) \leqslant \mathbb{E} \big[ f(X) \big],$$ as soon as the expectations exist. For a strictly convex function, there is equality if and only if \(X\) is almost surely constant. This is often stated with \(\mu\) taking finitely many values, like in the plot below.

Proof. Starting with the standard definition of convexity that corresponds to random variables that take only two values in \(C\), this can be extended by recursion to all random variables taking finitely many values, and then by a density argument, to all random variables. See the Wikipedia page.

Proof without words. As nicely explained in this blog post by Mark Reid, a simple argument based on epigraphs leads to the inequality for discrete measures supported on \(x_1,\dots,x_n\), with non-negative weights \(\lambda_1, \dots,\lambda_n\) that sum to one, with an illustration below for \(n=4\): any convex combination of points \((x_i,f(x_i))\) has to be in the red convex polygon, which is above the function.

A bit of history

The result is typically attributed to the Danish mathematician Johan Jensen [1, in French] who proved in 1906 the result for convex functions on the real line (in fact all continuous mid-point convex functions), but Otto Hölder had shown it earlier for twice differentiable functions [2, in German]. It turns out this was known thirty years earlier for uniform measures on finite sets, as shown by Jules Grolous [3], a relatively unknown former student from Ecole Polytechnique. See also [4] for more details on the history of Jensen’s inequality.

Classical applications

Jensen’s inequality can be used to derive many other classical inequalities, typically applied to the exponential, logarithm or powers.

Arithmetic, harmonic, and geometric means. For \(X\) with positive real values, we have: $$ \mathbb{E}[X]\geqslant \exp \Big( \mathbb{E}\big[ \log(X)\big]\Big) \ \mbox{ and } \ \mathbb{E}[X] \geqslant \frac{1}{\mathbb{E}\big[\frac{1}{X}\big]},$$ which corresponds for empirical measures to classical inequalities between means.

Young’s inequality. For \(p,q>1\) such that \(\frac{1}{p}+\frac{1}{q}=1\), and two non-negative real numbers \(x,y\), we get by Jensen’s inequality, $$ \log\big(\frac{1}{p} x^p + \frac{1}{q} y^q \big) \geqslant \frac{1}{p} \log(x^p) + \frac{1}{q} \log(y^q) = \log(xy),$$ leading to Young’s inequality \(\displaystyle xy \leqslant \frac{1}{p} x^p + \frac{1}{q} y^q.\)

Hölder’s inequality. For any positive \(x_1,\dots,x_n,y_1,\dots,y_n\), we can write $$\sum_{i=1}^n x_i y_i = \sum_{j=1}^n y_j^q \cdot \sum_{i=1}^n x_i y_i^{1-q} \frac{y_i^q}{\sum_{j=1}^n y_j^q} \leqslant \sum_{j=1}^n y_j^q \cdot \Big( \sum_{i=1}^n (x_i y_i^{1-q})^p \frac{y_i^q}{\sum_{j=1}^n y_j^q} \Big)^{1/p},$$ leading to Hölder’s inequality (with the same relationship between \(p\) and \(q\) as above): $$\sum_{i=1}^n x_i y_i \leqslant \Big( \sum_{j=1}^n y_j^q \Big)^{1/q} \Big( \sum_{j=1}^n x_j^p \Big)^{1/p}.$$ This includes also Cauchy-Schwarz inequality if \(p=q=2\), and also multiple versions of the “eta-trick“.

Majorization-minimization

Within data science, Jensen’s inequality is often used to derive auxiliary functions used in majorization-minimization algorithms, with two classical examples below.

Non-negative matrix factorization (NMF). Given a non-negative matrix \(V \in \mathbb{R}_+^{n \times d}\), the goal of NMF is to decompose it as \(V = WH\) with \(W \in \mathbb{R}_+^{n \times m}\) and \(H \in \mathbb{R}_+^{m \times d}\). This has many applications, in particular in source separation [5, 6].

A classical cost function which is used to estimate \(W\) and \(H\) is the Kullback-Leibler divergence [5] $$ D(V \| WH) = \sum_{i=1}^n \sum_{j=1}^d \Big\{ V_{ij} \log \frac{ V_{ij} }{ ( WH)_{ij} }\ – V_{ij} + (WH)_{ij} \Big\}.$$ To minimize the cost function above with respect to \(H\) only, the problematic term is \(\log ( WH)_{ij} = \log \big( \sum_{k=1}^m W_{ik} H_{kj} \big)\), which is a “log of a sum”. To turn it into a “sum of logs”, we use Jensen’s inequality for the logarithm, by introducing a probability vector \(q^{ij} \in \mathbb{R}_+^m\) (with non-negative values that sum to one), and lower-bounding $$ \log ( WH)_{ij} = \log \Big( \sum_{k=1}^m q^{ij}_k \frac{W_{ik} H_{kj} }{q^{ij}_k} \Big) \geqslant \sum_{k=1}^n q^{ij}_{k} \log \frac{W_{ik} H_{kj}}{q^{ij}_k}.$$ For a fixed \(H\), the bound is tight for \(\displaystyle q^{ij}_k = \frac{W_{ik} H_{kj}}{(WH)_{ij}},\) and given all \(q\)’s, we can minimize with respect to \(H_{ki}\) in closed form to get the update $$H_{kj} \leftarrow H_{kj} \frac{\sum_{i=1}^n \! V_{ij} W_{ik} \, /\, (WH)_{ij} }{\sum_{i’=1}^n \! W_{i’k}}.$$ Because we had a tight upper bound at the current \(H\) (before the update), this is a descent algorithm. We can derive a similar update for \(W\). As shown in [5], this is a simple parameter-free descent algorithm that converges to a stationary point, often referred to as a multiplicative update algorithm. See a convergence analysis in [7] and alternatives based on relative smoothness [8] or on primal-dual formulations [9, 10].

Expectation-maximization (EM). The exact same technique of introducing a probability vector within the log and using Jensen’s inequality is at the core of EM for latent variable models and variational inference (in fact NMF is simply a particular instance for a Poisson likelihood), which are two good topics for future posts (see here for a simple derivation of the “evidence lower bound“).

Information theory

Within information theory, the concavity of the logarithm and the use of Jensen’s inequality play a major role in most classical results, e.g., positivity of the Kullback-Leilbler divergence or data processing inequality. This also extends to all f-divergences.

Operator convexity

When considering convexity with respect to a generalized inequaility (such as based on the Löwner order), we can extend many of the classical formulas above (relationship between means, Young’s and Hölder’s inequality) to matrices. See earlier post for an introduction. For a certain set of functions (such as the square or the negative logarithm) \(f: \mathbb{R} \to \mathbb{R}\), then for a random symmetric matrix \(X\), we have (for the Löwner order): $$ f\big( \mathbb{E}[X] \big) \preccurlyeq \mathbb{E} \big[ f(X) \big].$$ An intriguing extension is the operator version of Jensen’s inequality [10], for potentially dependent random variables \((X,Y)\), where \(X\) is symmetric, and the sizes of \(X\) and \(Y\) are compatible: $$ f \Big( \mathbb{E} \big[ Y^\top X Y \big] \Big) \preccurlyeq \mathbb{E} \big[ Y^\top f(X) Y \big] \ \mbox{ as soon as } \ \mathbb{E}[ Y^\top Y ] = I.$$

Exact expression of the remainder

There is a large literature on extensions, refinements on Jensen’s inequality. I have a cute one of my own, which has probably been derived before. For twice differentiable functions \(f\), we can use Taylor formula with integral remainder on the segment between \(X\) and \(\mathbb{E}[X]\), leading to, with \(g(t) = f\big( t X + (1-t) \mathbb{E}[X]\big)\), $$g(1) = g(0) + g'(0) + \int_0^1 \! g^{\prime \prime}(t)(1-t)dt.$$ Taking expectations, this leads to $$\mathbb{E} \big[f(X)\big] – f\big( \mathbb{E}[X]\big) = \mathbb{E} \bigg[ \int_0^1 \! ( X – \mathbb{E}[X])^\top f^{\prime\prime}\big( t X + (1-t) \mathbb{E}[X]\big) ( X – \mathbb{E}[X]) (1-t) dt \bigg].$$ From this expression, we recover traditional refinements or reversing of the order if \(f^{\prime\prime}\) has bounded eigenvalues. This can for example be used also for characterizing the equality cases in non-strictly convex situations [11, page 31].

References

[1] Johan L. Jensen. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Mathematica, 30(1): 175–193, 1906.
[2] Otto Hölder, Ueber einen Mittelwerthssatz. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, (1):38-47, 1889.
[3] Jules Grolous. Un théorème sur les fonctions. L’Institut, Journal Universel des Sciences et des Sociétés Savantes en France et à l’Etranger, 3(153):401, 1875.
[4] D. S. Mitrinović and P. M. Vasić. The centroid method in inequalities. Publikacije Elektrotehničkog fakulteta. Serija Matematika i fizika 498/541:3-16, 1975.
[5] Daniel D. Lee and H. Sebastian Seung. Algorithms for non-negative matrix factorization. Advances in Neural Information Processing Systems, 13, 2000.
[6] Cédric Févotte, Nancy Bertin, and Jean-Louis Durrieu. Nonnegative matrix factorization with the Itakura-Saito divergence: With application to music analysis. Neural computation 21(3):793-830, 2009.
[6] Roland Badeau, Nancy Bertin, and Emmanuel Vincent. Stability analysis of multiplicative update algorithms and application to nonnegative matrix factorization. IEEE Transactions on Neural Networks, 21(12):1869-1881, 2010.
[7] Heinz H. Bauschke, Jérôme Bolte, and Marc Teboulle. A descent lemma beyond Lipschitz gradient continuity: first-order methods revisited and applications. Mathematics of Operations Research 42(2):330-348, 2017.
[8] Niao He, Zaid Harchaoui, Yichen Wang, and Le Song. Fast and simple optimization for Poisson likelihood models. Technical report, arXiv:1608.01264, 2016.
[9] Felipe Yanez and Francis Bach. Primal-dual algorithms for non-negative matrix factorization with the Kullback-Leibler divergence. International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2017.
[10] Frank Hansen, Gert K. Pedersen. Jensen’s Operator Inequality. Technical report, arXiv:0204049, 2002.
[11] Francis Bach. Information theory with kernel methods. IEEE Transactions in Information Theory, 69(2):752-775, 2022.