Playing with positive definite matrices – I: matrix monotony and convexity

In a series of a few blog posts, I will present classical and non-classical results on symmetric positive definite matrices. Beyond being mathematically exciting, they arise naturally a lot in machine learning and optimization, as Hessians of twice continuously differentiable convex functions and through kernel methods. In this post, I will focus on the benefits and perils of using the Löwner order between symmetric matrices as a tool for proving inequalities.

I will consider symmetric matrices \(A \in \mathbb{R}^{d \times d}\) of size \(d \times d\), denoting by \(\mathcal{S}_d\) the set all such matrices. There are many characterizations of symmetric positive semi-definite (PSD) matrices: (a) non-negative eigenvalues, (b) \(x^\top A x \geqslant 0\) for all \(x \in \mathbb{R}^d\), or (c) expression as a square as \(A = BB^\top\). Let’s denote this set by \(\mathcal{S}_d^+\).

A very useful tool in matrix analysis is the use of the Löwner order. It is defined as follows on \(\mathcal{S}_d\): $$ A \preccurlyeq B \Leftrightarrow B-A \in \mathcal{S}_d^+.$$ In other words, \(A\) is smaller than \(B\) if and only if \(B\, – A\) is positive semi-definite (PSD). The notation \(B \succcurlyeq A\) is defined as equivalent to \(A \preccurlyeq B\).

This defines a classical order relation which is reflexive (\(A \preccurlyeq A\) for all \(A\)), antisymmetric (for all \(A, B \in \mathcal{S}_d\), \(A \preccurlyeq B\) and \(B \preccurlyeq A\) imply \(A=B\)), and transitive (\(A \preccurlyeq B\) and \(B \preccurlyeq C\) imply \(A \preccurlyeq C\)).

Using operations on the Löwner order can make proofs much simpler, but it can also lead to atrocious mistakes. The main reason ends up being the lack of commutativity of the matrix product, that is, in general \(AB \neq BA\).

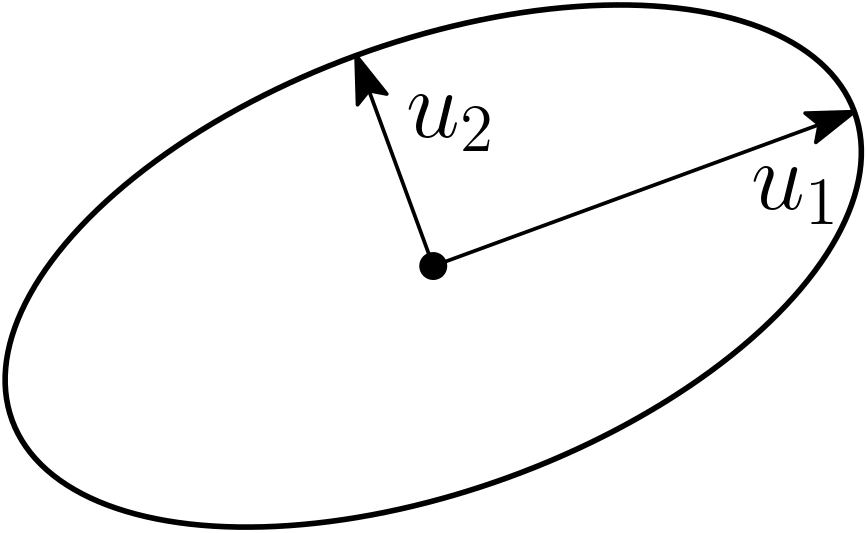
Representing positive matrices through ellipsoids. Any strictly PSD matrix \(A\) defines an ellipsoid $$ \mathcal{E}_A = \big\{ x \in \mathbb{R}^d, \ x^\top A^{-1} x \leqslant 1 \big\}$$ centered at zero. The eigenvectors are the traditional principal axes of the ellipsoid and the eigenvalues the squared lengths of these axes. See an illustration below with \(d = 2\), and the two eigenvectors \(u_1\) and \(u_2\).

The key property here is that \(\mathcal{E}_A \subset \mathcal{E}_B\) if and only if \(A \preccurlyeq B\). This representation immediately highlights that the order is partial. See examples below.

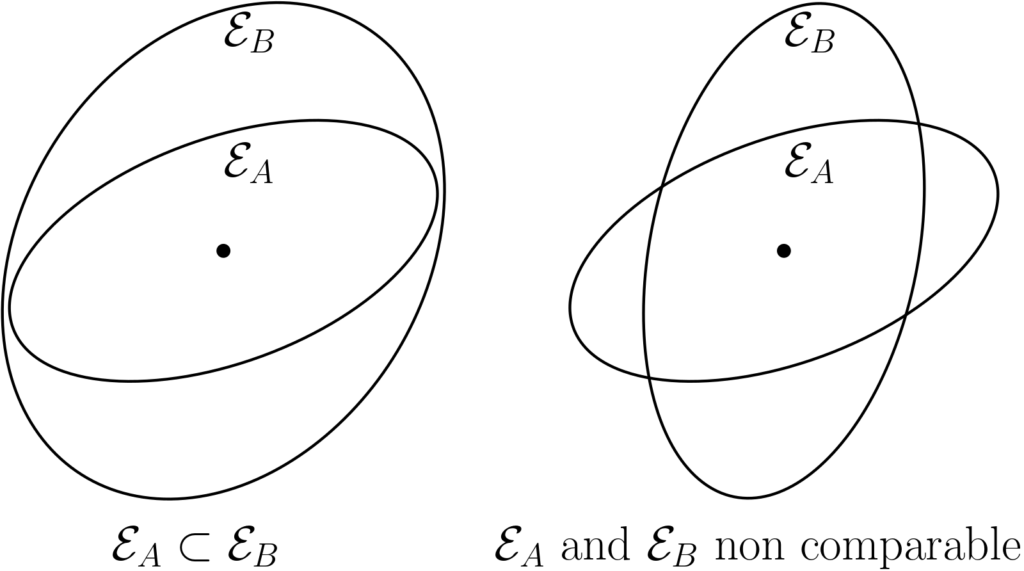
Moreover, if two matrices commute, then they are jointly diagonalizable, that is, the principal axes are aligned, and once expressed in the common eigenbasis, we obtain diagonal matrices, and we then have \({\rm Diag}(\lambda) \preccurlyeq {\rm Diag}(\mu)\) if and only if for all \(i\), \(\lambda_i \leqslant \mu_i\).

Several good books are available and reading them is both enjoyable and fruitful [1, 4, 10]. Let’s now look at some properties of this Löwner order.

Fun (and useful) facts and common mistakes

Here I list classical properties that are constantly used in proofs using positive matrices. This is crucially used in the analysis of gradient methods for least-squares [6, 7], as well as in analyzing linear dynamical systems, with control or not [8].

Direct consequence of the definition. For any \(d \times n\) matrix \(X\), and \(A,B \in \mathcal{S}_d\) such that \( A \preccurlyeq B\), $$ X^\top A X \preccurlyeq X^\top B X, $$ with the simple proof \(y^\top X^\top A X y = ( X y)^\top A ( X y) \leqslant ( X y)^\top B ( X y) = y^\top X^\top B X y \) for all \(y \in \mathbb{R}^n\).

Another similar formulation is $$ A \preccurlyeq B \Rightarrow {\rm tr}(AM) \leqslant {\rm tr} (BM) \mbox{ for all } M \succcurlyeq 0.$$ However this not true if \(M\) is not PSD. In particular, if \(A \preccurlyeq B\) we do not have in general for all \(x, y \in \mathbb{R}^d\), \(x^\top A y \leqslant x^\top B y \), which is a common mistake.

Another consequence, with \(X = B^{\, -1/2}\) the inverse of the square root of \(B\) (assuming that \(B\) is invertible), is \(A \preccurlyeq B \Rightarrow B^{\, -1/2} A B^{\, -1/2} \preccurlyeq I\).

Schur complements. A very useful identity is, for any rectangular matrix \(C\): $$ CC^\top \preccurlyeq I \Leftrightarrow C^\top C \preccurlyeq I.$$ This can be extended to (with matrices of proper sizes): $$ C B^{\, -1} C^\top \preccurlyeq A \Leftrightarrow C^\top A^{-1} C \preccurlyeq B$$ for PSD invertible matrices \(A, B\), both properties being equivalent to $$ \bigg( \begin{array}{cc} A & C \\ C^\top & B \end{array} \bigg) \succcurlyeq 0.$$ This is the usual characterization of positive-definiteness of block matrices through Schur complements.

Trace inequalities. If \(A \succcurlyeq 0 \) and \(B \succcurlyeq 0 \), then we have $$ 0 \leqslant {\rm tr}(AB) \leqslant {\rm tr(A)} \lambda_{\max}(B) \leqslant {\rm tr(A)} {\rm tr}(B).$$ Moreover, still if \(A \succcurlyeq 0 \) and \(B \succcurlyeq 0 \), $$ {\rm tr} (AB) \geqslant 0 \mbox{ with equality if and only if } AB=0.$$ This is used a lot in semi-definite programming, in particular for optimality conditions (see [9] for details), and can be shown (for the non-trivial direction) by using an eigenvalue decomposition of \(A\) as \(A = \sum_{i=1}^d \lambda_i u_i u_i^\top\), writing \({\rm tr}(AB) = \sum_{i=1}^d \lambda_i u_i^\top B_i u_i\), which is a sum of non-negative terms and thus if \({\rm tr}(AB)=0\), all terms have to be equal to zero, leading exactly to the result (since \(u^\top B u =0\) is equivalent to \(Bu=0\) when \(B \succcurlyeq 0\)).

Matrix functions

One particularly elegant and efficient way of using symmetric matrices is through matrix functions. Some are based on classical linear algebra such as the matrix inverse \(A^{\, -1}\), the matrix square root \(A^{1/2}\), or any polynomial or rational functions. Many others are defined as spectral functions. That is, given a function \(f:I \to \mathbb{R}\), defined on some interval \(I\) we can define for any symmetric matrix latex \(A \in \mathbb{S}_d\) with eigenvalue decomposition \(A = \sum_{i=1}^d \lambda_i u_i u_i^\top\), and all eigenvalues in \(I\): $$f(A) = \sum_{i=1}^d f(\lambda_i) u_i u_i^\top.$$

We get the usual definition of matrix powers \(A^p\), inverse \(A^{-1}\), but also logarithm \(\log A\) for PSD matrices, exponential \(\exp(A)\), etc. When the matrix is diagonal, then we apply the function on diagonal elements $$f({\rm Diag}(\lambda)) = {\rm Diag}(f(\lambda)).$$

For real numbers, a function \(f\) is non-decreasing if and only if for all \(\lambda,\mu\), $$ \lambda \leqslant \mu \Rightarrow f(\lambda) \leqslant f(\mu).$$ When \(f\) is non-decreasing, then for \(d=1\), we do have \(f(A) \preccurlyeq f(B)\) as soon as \(A \preccurlyeq B\). Moreover, when \(A\) and \(B\) commute, then can be jointly diagonalized, and then the property above is true for all non-decreasing functions. This is the same if we just want \({\rm tr} [ f(A) ] \leqslant {\rm tr}[f(B)]\).

When does it extend to \(d>1\), beyond taking the trace, and for non-commuting matrices? Functions for which $$ \forall A, B \in \mathcal{S}_d, \ A \preccurlyeq B \Rightarrow f(A) \preccurlyeq f(B)$$ for all dimensions \(d\) are called matrix-monotone. Let us start with a few positive examples with simple direct proofs.

Matrix inverse. If \( A \preccurlyeq B\) and \(A\) is invertible, then, \(B\) is invertible, and \(B^{\, -1/2} A B^{\, -1/2} \preccurlyeq I\), which is equivalent to \((A^{1/2} B^{\, -1/2})^\top A^{1/2} B^{\, -1/2} \preccurlyeq I\) and thus \(A^{1/2} B^{\, -1} A^{1/2} = A^{1/2} B^{\, -1/2} (A^{1/2} B^{\, -1/2})^\top \preccurlyeq I\), and then \(A^{\:\! -1} \succcurlyeq B^{\, -1} \). The function \(\lambda \mapsto -\lambda^{-1}\) is thus matrix-monotone.

Matrix square root. From the paragraph above, if \( A \preccurlyeq B\) and \(A\) is invertible, then \(\|A^{1/2} B^{\, -1/2} \|_{\rm op} \leqslant 1\), thus all (potentially complex) eigenvalues of \(A^{1/2} B^{\, -1/2}\) have magnitude less than one, and thus this is the same for all eigenvalues of the similar matrix \(B^{\, -1/4} ( A^{1/2} B^{\, -1/2} ) B^{1/4}= B^{\, -1/4} A^{1/2} B^{\, -1/4}\), which finally implies \(B^{\, -1/4} A^{1/2} B^{\, -1/4} \preccurlyeq I\), and thus \(A^{1/2} \preccurlyeq B^{1/2}\). The function \(\lambda \mapsto \lambda^{1/2}\) is thus matrix-monotone.

Matrix square. “Unfortunately” \(A \succcurlyeq B \succcurlyeq 0\) does not imply \(A^2 \succcurlyeq B^2\). This is a very common mistake! (I have made it at several occasions).

In fact, this is rarely true, indeed, if \(B = A + \Delta\), we have \(B^2 – A^2 = \Delta^2 + A \Delta + \Delta A,\) and as soon as the column space of \(\Delta\) does not contain the one of \(A\), the equality between squares is impossible. See an illustration below in two dimensions.

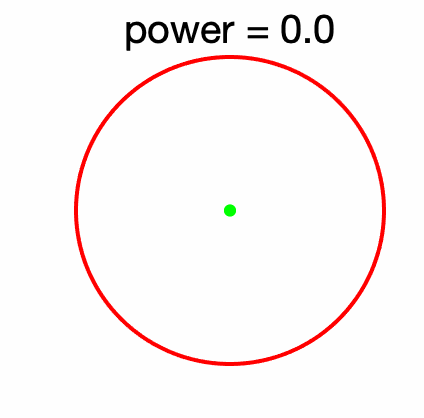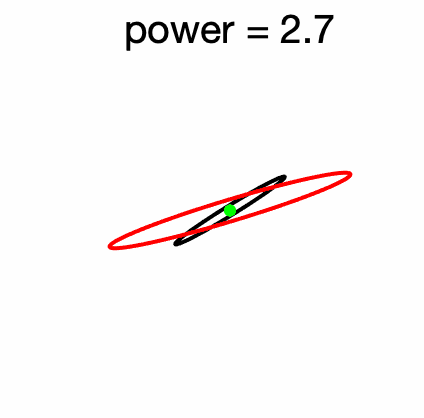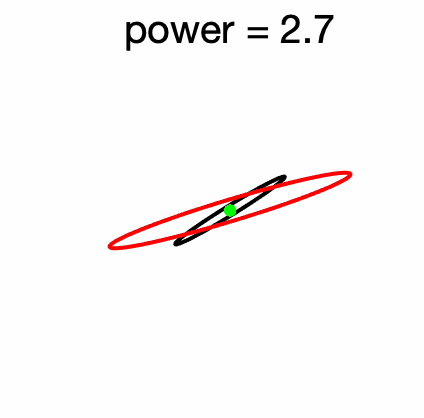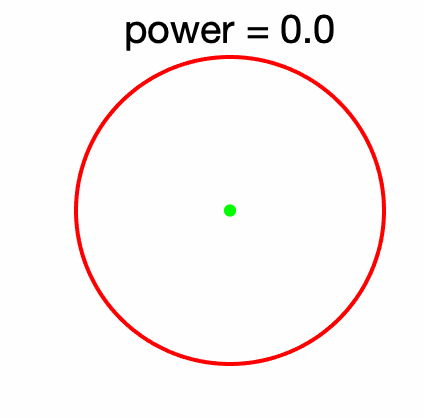
Luckily, as mentioned by my colleague Alessandro Rudi, for any incorrect matrix inequality, there is a close by true inequality. Here, for example, we have that \(A \succcurlyeq B \succcurlyeq 0\) does imply \({\rm tr}(A^2) \geqslant {\rm tr}(B^2)\) (as can be seen by from the positivity of the trace of products of PSD matrices). Moreover, there are the so-called Furuta inequalities, (see Corollary 1.18 in [4]): $$ A \succcurlyeq B \succcurlyeq 0 \Rightarrow A^2 \succcurlyeq ( AB^2A)^{1/2} \mbox{ and } (BA^2B)^{1/2} \succcurlyeq B^2, $$ which can prove useful.

Towards a characterization of matrix-monotone functions. We have seen that \(\lambda \mapsto \lambda^2\) is not matrix-monotone, while \(\lambda \mapsto \lambda^{1/2}\) and \(\lambda \mapsto -1/\lambda\) are. So what functions are matrix monotone? It turns out that there is a general answer, which is an amazing result from Löwner: he gives a precise characterization of matrix-monotone functions [2], with a whole book [3] about it with 11 different proofs!

Positivity of Löwner matrices

We start with a first characterization that will please the kernel enthusiasts. The question here is as follows. Given a differentiable function \(f: I \to \mathbb{R}\), and \(n\) real numbers \(\lambda_1,\dots,\lambda_n \in I\) the domain of \(f\), when is the \(n \times n\) matrix \(L\) with values $$L_{ij} = \frac{f(\lambda_i)-f(\lambda_j)}{\lambda_i – \lambda_j} \mbox{ for } i \neq j,$$ and \(L_{ii} = f'(\lambda_i)\), always positive semi-definite? These matrices are called Löwner matrices and it turns out that the differentiable functions \(f\) for which all Löwner matrices are PSD are exactly the matrix-monotone functions.

To see this, we simply need to compute the derivative at \(t=0\) of the matrix-valued function \(g: [0,1] \to \mathcal{S}_d\) defined as $$g(t) = f(A + t(B-A)).$$ Using a former blog post, we have with the eigenvalue decomposition \(A=\sum_{i=1}^d \! \lambda_i u_i u_i^\top\), $$g'(0) = \sum_{i,j=1}^d \frac{f(\lambda_i)-f(\lambda_j)}{\lambda_i – \lambda_j} u_i^\top (B-A)u_j,$$ with the convention that for \(i=j\), \(\frac{f(\lambda_i)-f(\lambda_j)}{\lambda_i – \lambda_j} = f'(\lambda_i)\). Therefore, \(g'(0) = \sum_{i,j=1}^d L_{ij} u_i^\top (B-A)u_j\).

Thus, if \(f\) is matrix-monotone, we have \(g'(0) \geqslant 0\), and by choosing \(A = {\rm Diag}(\lambda)\) diagonal and \(B\, – A = zz^\top\) rank-one, we get \(g'(0) = \sum_{i,j=1}^d L_{ij} z_i z_j \geqslant 0\), which leads to the positivity of \(L\) since this is true for any vector \(z \in \mathbb{R}^n\).

In the other direction, if \(L \succcurlyeq 0\) all Löwner matrices are PSD, then as soon as \(B-A \succcurlyeq 0\), we can then get with a similar reasoning \(g'(t) \geqslant 0\) for \(t \in [0,1]\), and thus \(f(B) = g(1) \geqslant g(0) = f(A)\), which shows monotonicity.

Note that, like all generic results on positive-definiteness of matrices (like Bochner theorem), this is an infinite source of “problèmes de colle” (oral mathematical exams which are common in France).

Characterizing all matrix-monotone functions

There are many different characterizations of matrix monotonicity (see [3]). I will only mention a simple intuitive result for \(I = (0,+\infty)\), with a sketch of a particularly elegant proof coming from [5].

A family of non-negative monotone functions. As seen above, the function \(\lambda \mapsto -1/\lambda\) is matrix-monotone on \(\mathbb{R}_+^\ast\). So is \(\lambda \mapsto \frac{\lambda}{(1-t)\lambda+t}\) for any \(t \in [0,1]\). Moreover, for all \(t \in [0,1]\), these functions are non-negative on \(\mathbb{R}_+^\ast\) and the value at 1 is 1. Note that with \(t=1\), we recover \(\lambda \mapsto \lambda\), while for \(t=0\), we recover \(\lambda \mapsto 1\).

Since matrix-monotonicity is a property which is invariant by taking convex combinations of functions, all functions of the form $$ \lambda \mapsto \int_{0}^{1}\frac{\lambda}{(1-t)\lambda+t}d\mu(t)$$ for a probability measure \(\mu\) on \([ 0 , 1 ]\), are also matrix-monotone, non-negative and with value 1 at 1. It turns out we cover them all! The argument is based on showing that the functions \(\lambda \mapsto \frac{\lambda}{(1-t)\lambda+t}\) are the extreme points of the of functions defined above. See details in [5].

We can then recover all matrix-monotone functions on \( (0,+\infty)\) by adding a constant and letting the mass of \(\mu\) be different from one (and potentially infinite). By making the change of variable \(u = t / (1-t)\), we get the representation as $$f(\lambda) = \alpha + \beta (\lambda-1) + (\lambda-1) \int_0^\infty \!\!\frac{ 1 }{\lambda + u} d\nu(u)$$ for some positive measure \(\nu\) and \(\beta>0\). For example, we have: $$ \log \lambda = (\lambda-1) \int_0^{+\infty} \!\!\frac{1}{\lambda +u} \frac{du}{1+u},$$ and for \(p \in (0,1]\), $$ \lambda^p = 1 + (\lambda-1) \frac{ \sin p \pi}{\pi} \int_0^{+\infty} \!\!\frac{1}{\lambda+u} u^{p-1} du,$$ showing the matrix-monotonicity of the logarithm and of certain powers. Note that the exponential function is not matrix-monotone, and that the only powers \(p \neq 0\) such that \(\lambda \mapsto \lambda^p\) or \(\lambda \mapsto -\lambda^p\) are matrix-monotone are \(p \in (0,1]\) and \(p \in [-1, 0)\).

Matrix-convex functions

Similarly to matrix-monotone functions, matrix-convex functions are functions for which $$ \forall A, B \in \mathcal{S}_d, \forall \lambda \in [0,1], \ f( \lambda A + (1-\lambda) B) \preccurlyeq \lambda f(A) + ( 1-\lambda) f(B).$$ Like for real-valued functions, there is an intimate link between monotonicity and convexity here. Indeed, one can show that \(f\) is matrix-convex on the interval \(I\) if and only if for all \(\mu \in I\), the function \(\lambda \mapsto \frac{f(\lambda)-f(\mu)}{\lambda-\mu}\) is matrix-monotone (this is one of these cases where a natural property extends to the matrix case). Using similar arguments than for matrix-monotone functions, all functions of the form $$f(\lambda) = \gamma + \alpha (\lambda-1) + \beta (\lambda-1)^2 + (\lambda-1)^2 \int_0^\infty \!\!\frac{ 1 }{\lambda + u} d\nu(u)$$ for some positive measure \(\nu\) on \([0,+\infty)\) with finite mass, and \(\beta>0\) are matrix-convex on \((0,\infty)\). They also happen to be the only ones (see, e.g., [11]).

The classical examples are then \(f(\lambda) = \, – \log \lambda\), \(f(\lambda) = \lambda \log \lambda\), \(f(\lambda) = \lambda^p\) for \(p \in [1,2]\) and \(p \in [-1,0)\).

Note that like for monotonicity, if we just want the real-valued function \(A \mapsto {\rm tr} [ f(A)]\) to be convex, this is equivalent to \(f\) being convex.

Beyond spectral functions. There are many nice matrix convex functions beyond spectral functions: for example (see [12]) \(A \mapsto A^{-1} \) or \(A \mapsto A^2 \). Among ones that come up naturally: $$ (A,B) \mapsto A B^{\, -1} A$$ $$ (A,B) \mapsto\ – (A^{-1} + B^{\, -1})^{-1} $$ $$ (A,B) \mapsto\ – A^{1/2} ( A^{-1/2} B A^{-1/2} )^{1/2} A^{1/2} .$$ Add your favorite one!

Conclusion

Next months, we will see applications of matrix monotonicity and convexity, from sharp concentration inequalities for eigenvalues of random matrices [13] to a brand new mix of (quantum) information theory and kernels methods [14].

Acknowledgements. I would like to thank Alessandro Rudi for fruitful discussions, and Loucas Pillaud-Vivien for proofreading this blog post and making good clarifying suggestions.

References

[1] Rajendra Bhatia. Positive Definite Matrices. Princeton University Press, 2009.
[2] Karl T. Löwner. Über monotone Matrixfunktionen. Mathematische Zeitschrift, 38:177-216, 1934.
[3] Barry Simon. Löwner’s Theorem on Monotone Matrix Functions. Springer, 2019.
[4] Xingzhi Zhan. Matrix inequalities. Springer Science & Business Media, 2002.
[5] Frank Hansen. The fast track to Löwner’s theorem. Linear Algebra and its Applications 438.11: 4557-4571, 2013.
[6] Francis Bach and Eric Moulines. Non-strongly-convex smooth stochastic approximation with convergence rate \(O(1/n)\). Advances in Neural Information Processing Systems 26, 2013.
[7] Aymeric Dieuleveut, Nicolas Flammarion, and Francis Bach. Harder, Better, Faster, Stronger Convergence Rates for Least-Squares Regression. Journal of Machine Learning Research, 18(101):1−51, 2017.
[8] Stephen Boyd, Laurent El Ghaoui, Eric Feron, and Venkataramanan Balakrishna. Linear Matrix Inequalities in System and Control Theory. SIAM, 1994.
[9] Lieven Vandenberghe, Stephen Boyd. Semidefinite Programming. SIAM Review, 38:49–95.
[10] Rajendra Bhatia. Matrix analysis. Springer Science & Business Media, 2013.
[11] Andrew Lesniewski and Mary Beth Ruskai. Monotone Riemannian metrics and relative entropy on noncommutative probability spaces. Journal of Mathematical Physics, 40(11):5702–5724, 1999.
[12] Tsuyoshi Ando. Concavity of certain maps on positive definite matrices and applications to Hadamard products. Linear algebra and its applications, 26: 203-241, 1979.
[13] Joel A. Tropp. An introduction to matrix concentration inequalities. Foundations and Trends in Machine Learning, 8(1-2):1–230, 2015.
[14] Francis Bach. Information Theory with Kernel Methods. Technical Report, arXiv-2202.08545, 2022.