Non-convex quadratic optimization problems

Among continuous optimization problems, convex problems (with convex objectives and convex constraints) define a class that can be solved efficiently with a variety of algorithms and with arbitrary precision. This is not true more generally when the convexity assumption is removed (see this post). This of course does not mean that (1) nobody should attempt to solve high-dimensional non-convex problems (in fact, the spell checker run on this document was trained solving such a problem…), and that (2) no other problems have efficient solutions.

In this post, we will look at a classical class of continuous optimization problems that can be solved efficiently, namely quadratic optimization problems on the Euclidean sphere or ball. That is, we look at solving $$\tag{1} \min_{ \| x\| \leqslant 1} \ \frac{1}{2} x^\top A x \ – b^\top x, $$ and $$\tag{2} \min_{ \| x\| = 1} \ \frac{1}{2} x^\top A x \ – b^\top x, $$ for \(\|x\|^2 = x^\top x\) the standard squared Euclidean norm.

The matrix \(A \in \mathbb{R}^{n \times n}\) is assumed only symmetric (no need to be positive semi-definite), and \(b \in \mathbb{R}^n\). Therefore, the objective may not be convex, and the constraint set (in the case of the sphere), is not convex either. We could replace the standard squared Euclidean norm \(x^\top x\) by any Mahanalobis squared norm \(x^\top B x\) for \(B\) positive-definite, but to keep it simple, let’s only consider \(B = I\).

Note that there are other continuous non-convex optimization problems that can be solved efficiently through a convex reformulation, such as the minimization of one-dimensional (trigonometric) polynomials, and more generally sum-of-squares problems (see this post). If you are aware of many more beyond combinatorial optimization problems, please let me know.

Special case of eigenvalues. If \(b=0\) (no linear term), then the solution of Problem \((2)\) is the eigenvector associated with the smallest eigenvalue of \(A\), while the solution of Problem \((1)\) is the same eigenvector if the smallest eigenvalue of \(A\) is negative, and zero otherwise. This has a large number of applications, is the topic of tons of “spectral relaxation” works, and will not be the focus of this post.

Applications

Problems \((1)\) and \((2)\) appear in several areas and first appeared in [2] in 1965 (if you know of an earlier reference, please let me know). The three main occurrences that I am aware of are in trust-region methods, constrained eigenvalue problems, and relaxation of binary optimization problems.

Trust-region methods. When minimizing a differentiable function \(f\) on \(\mathbb{R}^n\), the classical gradient descent iteration $$x^+ = x \, – \gamma f(x)$$ can be seen as the solution of $$\min_{y \in \mathbb{R}^n} \ f(x) + f'(x)^\top ( y\, – x ) \mbox{ such that } \| y\, – x\| \leqslant \delta,$$ for \(\delta = \gamma \| f'(x)\|_2\). This corresponds to minimizing the first-order Taylor expansion in a ball centered at \(x\), and leads to the minimization of an affine function on an Euclidean ball. When using the second order model, we get to solve $$\min_{y \in \mathbb{R}^n} \ f(x) + f'(x)^\top ( y \, – x ) + \frac{1}{2} ( y\, -x )^\top f^{\prime \prime}(x) ( y \, -x ) \mbox{ such that } \| y \, – x\| \leqslant \delta, $$ which can be cast as Problem \((1)\).

The intuitive idea is that the Taylor expansion is only local, so we optimize it locally, instead of globally, like the classical Newton method would do. Moreover, it is well-defined even for singular Hessians. See figure below and [4] for more details.

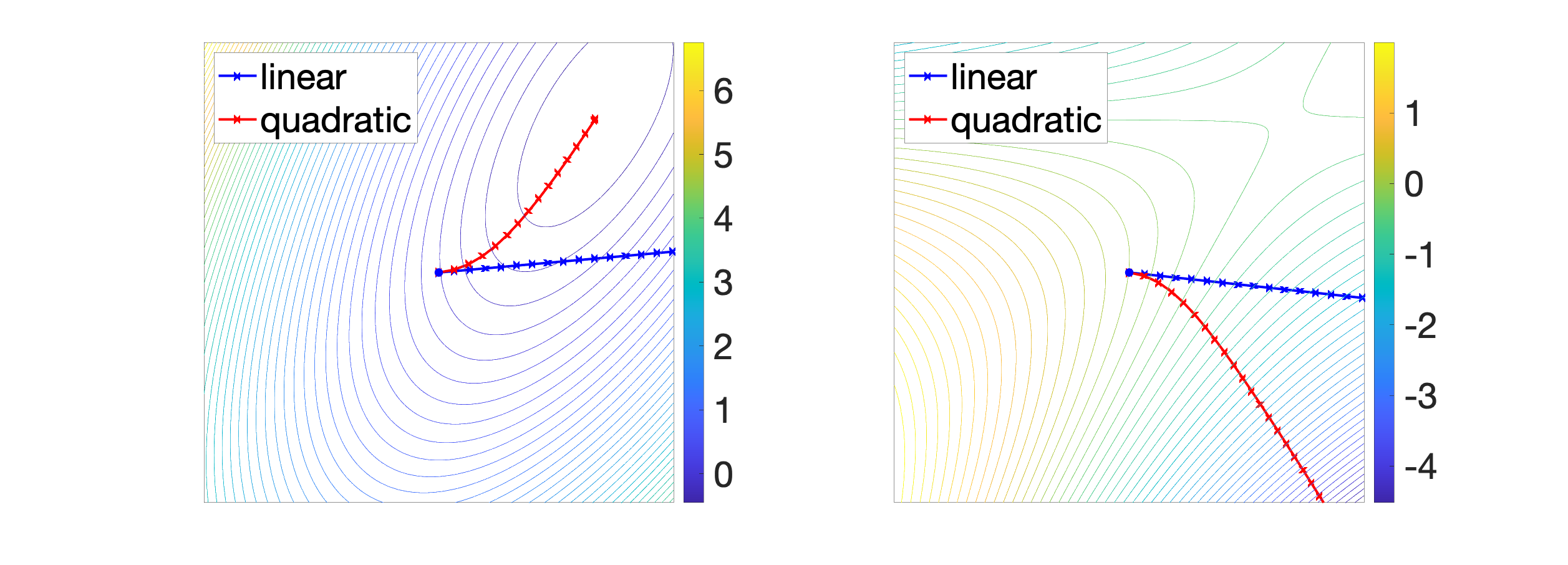
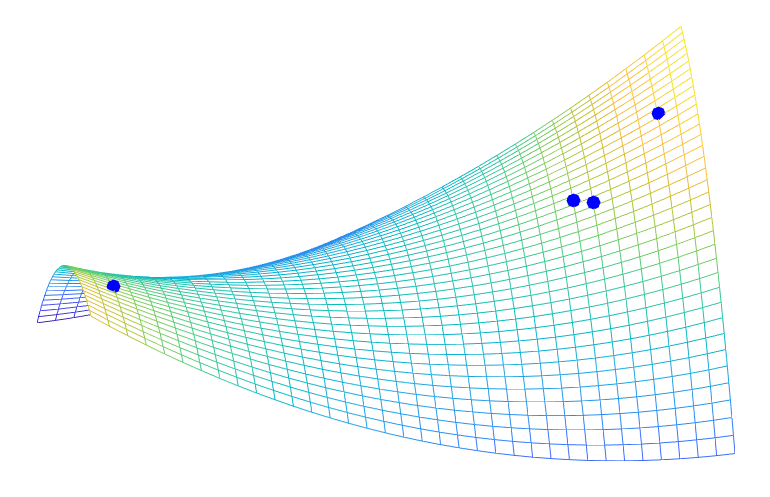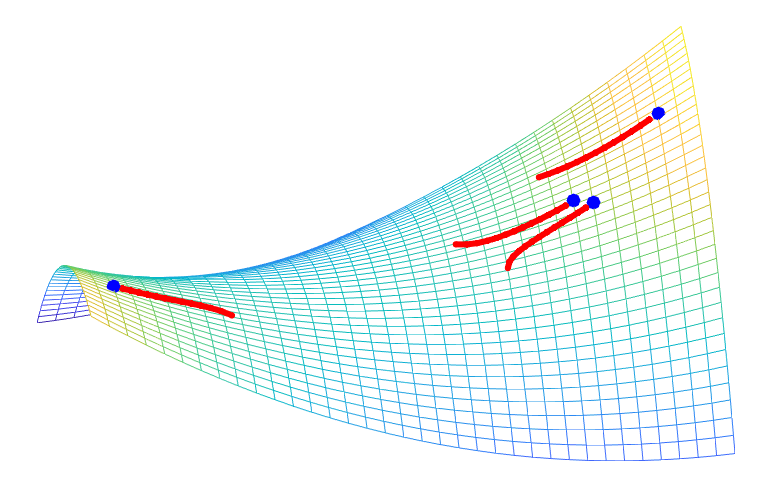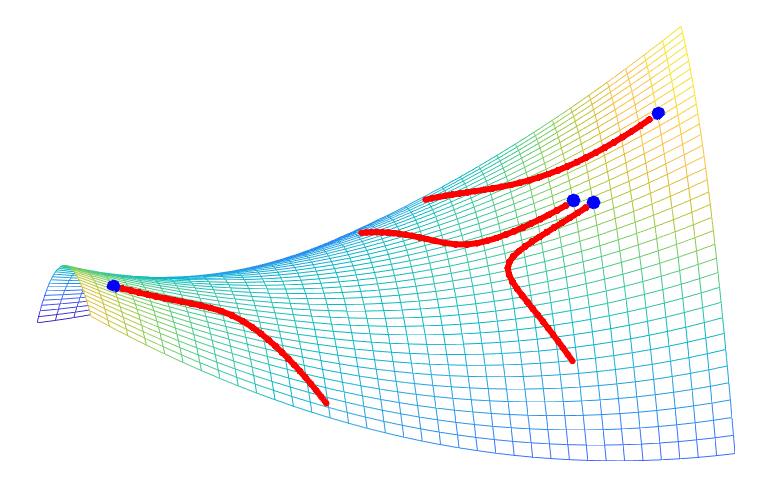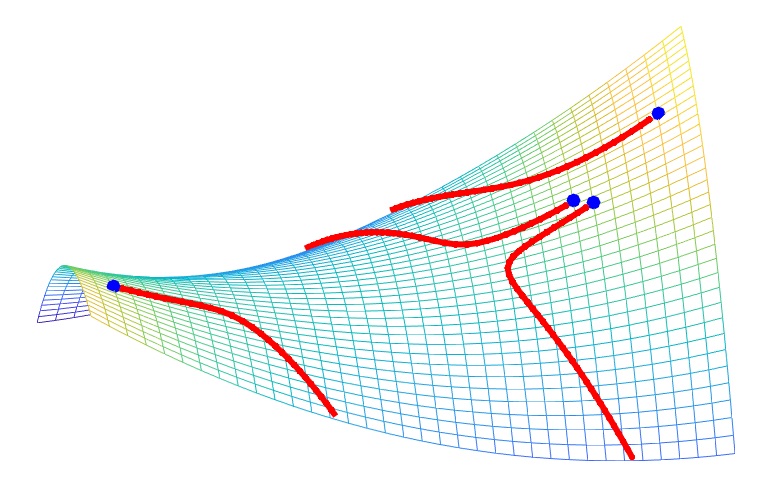
Constrained eigenvalue problems. If we aim to minimize \(x^\top A x\) subject to \(x^\top x = 1\) and an affine constraint [3], then, by writing the affine constraint as \(x = Cz+d\), we obtain the minimization of a quadratic-linear function subject to a quadratic-linear constraint, which we can rewrite in a form similar to Problem \((2)\).

Relaxation of binary optimization problems. When minimizing a linear-quadratic function on \(\{-1,1\}^n\), we can relax it by replacing the constraint \(x \in \{-1,1\}^n\) by \(x^\top x = n\).

From local to global optimality conditions

Let’s now look at optimality conditions from first principles (see [5, 6] for more details), before relating them to a broader discussion on tight semi-definite relaxations.

Existence of minimizers. Minimizers always exists for \(f(x) = \frac{1}{2} x^\top A x \ – b^\top x\) since the two sets \(\mathbb{S} = \{ x \in \mathbb{R}^n, x^\top x = 1\}\) and \(\mathbb{B} = \{ x \in \mathbb{R}^n, x^\top x \leqslant 1\}\) are compact. Therefore, the problems are well-formulated.

First-order necessary conditions on the sphere. We consider an optimal \(x \in \mathbb{S}\). For any \(y \in \mathbb{S}\) which is orthogonal to \(x\), and any \(\theta \in \mathbb{R}\), we have: $$f( \cos \theta \cdot x + \sin \theta \cdot y) = f(x) + f'(x)^\top y \cdot \theta + o(\theta).$$ Thus, since \(\cos \theta \cdot x + \sin \theta \cdot y\) is always on \(\mathbb{S}\), we must have \(f'(x)^\top y=0\), and this holds for all \(y\) orthogonal to \(x\). Thus \(f'(x)\) has to be proportional to \(x\), that is, there exists \(\mu \in \mathbb{R}\) such that \(f'(x) + \mu x = 0\), that is, \((A + \mu I) x = b\).

First-order necessary conditions on the ball. If \(x \in \mathbb{B}\) is optimal and in the interior, that is, \(x^\top x < 1\), then we directly have \(f'(x) = 0\). If \(x \in \mathbb{S}\), it has to be optimal for the sphere, and thus there exists \(\mu \in \mathbb{R}\) such that \(f'(x) + \mu x = 0\). By considering that \(g: t \mapsto f(t x)\) has to be minimized on \([0,1]\), for \(t=1\), we must have \(g'(1) \leqslant 0\), i.e., \(\mu = \, – f'(x) ^\top x \geqslant 0\).

In order to cover the interior case, we need to add the “complementary slackness” condition \(\mu ( 1 -x^\top x)=0\).

Obtaining necessary conditions from Lagrange duality. We can obtain the same first-order optimality conditions using Lagrange duality, by adding a Lagrange multiplier \(\mu \in \mathbb{R}\) for the equality constraint \(x^\top x = 1\), or \(\mu \in \mathbb{R}_+\) for the inequality constraint \(x^\top x \leqslant 1\), and forming the Lagrangian $$\tag{3} \mathcal{L}(x,\mu) = \frac{1}{2} x^\top A x\, – b^\top x + \frac{1}{2} \mu ( x^\top x\, – 1).$$ A necessary condition is thus that the partial derivative with respect to \(x\) is zero for a certain \(\mu\), which is exactly the condition \(f'(x) + \mu x = 0\) above.

Second-order conditions on the sphere. Assuming that \(f'(x) + \mu x = 0\), with \(\mu\) potentially negative (i.e., the first-order optimality conditions are satisfied), we then have, for any \(y \in \mathbb{S}\), $$\begin{array}{rcl}f(y) & = & f(x) + f'(x)^\top(y-x) + \frac{1}{2}(x-y)^\top A ( x-y) \\ & = & f(x) + \frac{1}{2}(x-y)^\top ( A + \mu I) ( x-y) + \frac{\mu}{2} ( x^\top x – y^\top y). \end{array}$$ Thus, if \(x\) is optimal, we must have \((x-y)^\top ( A + \mu I) ( x-y) \geqslant 0\) for all \(y \in \mathbb{S}\), which implies that \(A+ \mu I \succcurlyeq 0\). Note that our reasoning implies that the optimality condition, that is, existence of \(\mu \in \mathbb{R}\) such that $$\begin{array}{l} ( A+ \mu I) x = b \\ A+ \mu I \succcurlyeq 0 \\ x^\top x = 1 , \end{array} $$ is necessary and sufficient for the optimality of \(x\). The sufficiency can also be obtained through Karush-Kuhn-Tucker (KKT) conditions, which apply regardless of convexity. This is one of few problems where strong duality holds for a non-convex optimization problems.

Second-order necessary condition on the ball. We also get the following necessary and sufficient condition, that is, the existence of \(\mu \in \mathbb{R}_+\) such that $$\begin{array}{l} ( A+ \mu I) x = b \\ A+ \mu I \succcurlyeq 0 \\ x^\top x \leqslant 1 \\ \mu \, ( 1 \, – \, x^\top x) = 0. \end{array}$$

In both cases, once \(\mu\) is known, we can recover the optimizers \(x\). We now focus on the sphere for simplicity.

Equivalence to a one-dimensional problem

We can define the function \((M,u) \mapsto u^\top M^{-1} u\) as the minimal \(t \in \mathbb{R}\) such that the matrix \(\bigg( \begin{array}{cc} \!M\!\! & \!u\! \\[-.1cm] \!u^\top \!\! & \! t \! \end{array} \bigg) \succcurlyeq 0\). It is thus jointly convex in \((M,u)\), is infinite when \(M\) is not positive-semidefinite (PSD). When \(M\) is PSD but not invertible, the function is finite if and only if \(u\) is in the column space of \(M\). We can define similarly \(u^\top M^{-2} u\).

We can now get the dual problem associated to the Lagrangian in \((3)\), by minimizing it with respect to \(x\), leading to $$\max_{\mu \in \mathbb{R}} \ – \frac{\mu}{2} \, – \frac{1}{2} b^\top ( A+\mu I)^{-1} b, $$ which is a concave maximization problem in one dimension (with the constraint that \(A + \mu I \succcurlyeq 0\)).

Thus, a simple algorithm for solving the problem is to solve this one-dimensional concave maximization problem. Once an eigenvalue decomposition \(A = \sum_{i=1}^n \! \lambda_i u_i u_i^\top\) has been obtained, we need to maximize $$ \tag{4} – \frac{\mu}{2} \, – \frac{1}{2} \sum_{i=1}^n \frac{ (b^\top u_i)^2}{\lambda_i + \mu}. $$

Assuming that \(\lambda_1 \geqslant \lambda_2 \geqslant \cdots \geqslant \lambda_n\), we have the constraint \(\lambda_n + \mu \geqslant 0\). We first need to check if \(\mu = \, – \lambda_n\) is the solution, which occurs when \(b^\top ( A+ \mu I)^{-2} b \leqslant 1\) (the problem is then called “degenerate”, and this can only happen if \(b\) in the eigensubspace of \(A\) associated with eigenvalue \(– \lambda_n\), which is rather uncommon). Otherwise, the maximum is attained at \(\mu > -\lambda_n\) (note that since we have assumed \(b \neq 0\), the problem is strictly concave and thus has a unique maximizer in \(\mu\)). Moreover, \(\mu\) is characterized by the equation $$ \tag{5} b^\top ( A+ \mu I)^{-2} b = 1,$$ which can be obtained directly from the optimality conditions.

This one-dimensional problem can be solved using Newton’s method [6, 7] to estimate \(\mu\) given the eigendecomposition of \(A\). There are also cheaper less precise algorithms that do not require a full eigendecomposition. We will also see below a surprising reformulation as a simple eigenvalue problem.

Other “secular” equations. Equation \((5)\) is often referred to a secular equation. There are other types of similar equations, in particular for rank-one perturbations of the symmetric eigenvalue problem [8, 9].

Semi-definite relaxations

We can now give a more modern take on the quadratic maximization problem on the sphere, using semi-definite programming. We can first rewrite the objective function in Equation \((1)\) as $$f(x) = \frac{1}{2}x^\top A x \, – b^\top x = \frac{1}{2} {\rm tr}(AX) \, – b^\top x, $$ with \(X = xx^\top\). We now have a linear objective in \((X,x)\). Moreover, the matrix \(X\) satisfies the convex constraints $$ X \succcurlyeq xx^\top \Leftrightarrow \left( \begin{array}{cc} \!X\!\! & \!x\! \\[-.1cm] \!x^\top \!\!&\! 1\! \end{array} \right) \succcurlyeq 0, $$ and \({\rm tr}(X) = x^\top x = 1\). However the rank-one constraint is not convex.

A classical tool in optimization is to remove the rank-one constraint, and only obtain a lower bound (a so-called “relaxation”), with the following optimization problem: $$\tag{6} \min_{ X, x} \frac{1}{2} {\rm tr}(AX)-b^\top x \mbox{ such that } \left( \begin{array}{cc} \!X\!\! & \!x\! \\[-.1cm] \!x^\top \!\!&\! 1\! \end{array} \right) \succcurlyeq 0 \mbox{ and } {\rm tr}(X)=1. $$ One can check that the dual problem is exactly Equation \((4)\), and thus the relaxation is here tight. Moreover, the SDP formulation can be used to derive algorithms that do not need a full eigenvalue decomposition [12].

Semi-definite relaxation of QCQP’s. Problems \((1)\) and \((2)\) are in fact instances of quadratically constrained quadratic programming problems, and the problem \((6)\) is the usual semi-definite relaxation. It turns out that with a single constraint, such relaxations are always tight, owing to the S-lemma [10] (see a nice derivation in Boyd and Vandenberghe’s book [11, Appendix B.1]).

Tight sum-of-squares relaxation. Yet another reformulation is through sum-of-squares (see an earlier post), where we consider the feature vector \(\varphi(x) = {x \choose 1}\) and represent non-negative functions as quadratic forms \(x \mapsto \varphi(x)^\top B \varphi(x)\). The problem in \((2)\) can then be relaxed as $$\max_{c \in \mathbb{R}, \ B \succcurlyeq 0} c \ \mbox{ such that } \ f(x) \, – c = \varphi(x)^\top B \varphi(x),$$ which is exactly the tight SDP relaxation above.

Having fun with adding affine constraints. Recently I had to look at Problem \((2)\) with an extra affine constraint, which I will take for simplicity of the form \(c^\top x = 1\) (for a vector \(c \in \mathbb{R}^n\) such that \(\|c\| > 1\) to avoid a trivial problem). By projecting on the subspace orthogonal to \(c \in \mathbb{R}^n\), we obtain again a quadratic minimization problem, this time on a Euclidean sphere embedded in a space of dimension \(n-1\). Therefore, we can apply the above techniques on the reduced problem. However, I did not want to do that and wanted keep the original formulation on \(\mathbb{R}^n\), and then tried to use duality to solve it. Two natural possibilities emerge here.

In order to solve it, we could first imagine using Lagrange duality, with a Lagrange multiplier \(\mu\) for the constraint \(x^\top x = 1\) (this worked exactly without the extra affine constraint), and now an extra Lagrange multiplier \(\nu\) for the constraint \(c^\top x = 1\). This leads to the Lagrangian $$ \mathcal{L}(x,\mu,\nu) = \frac{1}{2} x^\top A x\, – b^\top x + \frac{1}{2} \mu ( x^\top x\, – 1) + \nu( c^\top x -1),$$ and thus, after a short calculation, the dual problem $$\max_{\mu,\nu \in \mathbb{R}} \ -\frac{\mu}{2} \, – \nu \, – \frac{1}{2} (b \, – \nu c)^\top ( A + \mu I)^{-1} (b \, – \nu c).$$ Another Lagrangian can be obtained with the equivalent constraint \((c^\top x\, – 1)^2 = 0\), leading to a new Lagrangian $$ \mathcal{L}'(x,\mu,\nu’) = \frac{1}{2} x^\top A x\, -b^\top x + \frac{1}{2} \mu ( x^\top x\, – 1) + \frac{1}{2} \nu’ (c^\top x \, – 1)^2,$$ and then the dual problem $$\max_{\mu,\nu’ \in \mathbb{R}} \ -\frac{\mu}{2} \, -\frac{\nu’}{2} \, – \frac{1}{2} (b+\nu’ c)^\top ( A + \nu’ cc^\top + \mu I)^{-1} (b+\nu’ c).$$ Are they both tight? Make up your own mind and see the bottom of the post for the answer.

Amazing eigenvalue reformulations

The Newton method to solve the one-dimensional problem is efficient, but requires some safeguards to work properly, and a full eigenvalue decomposition. It turns out that one can obtain exact reformulations as eigenvalue problems for a single eigenvalue, for which efficient packages exist.

From [3], for the optimization on the sphere, we can obtain the optimal \(\mu\) from the largest real eigenvalue of the following non symmetric matrix: $$\left( \begin{array}{cc} \!-A\! & \!\! I\! \\[-.1cm] \! bb^\top \!& \!\! -A\! \end{array} \right).$$ Indeed, one can check that, in the non-degenerate case, given the optimal \((x,\mu)\), then \(y = \left( \begin{array}{c} \!(A+\mu I)^{-1} x \! \\[-.1cm] x \end{array} \right)\) is an eigenvector of the \(2n \times 2n\) matrix above, with eigenvalue \(\mu\).

This leads to two lines of code to solve the problem, at least for the non-degenerate case! See more details in [3, 14], in particular, to deal with the degenerate case, often called the “hard case”. See the code snippets in Matlab, Julia, and Python.

Matlab	[y,mu] = eigs([-A, eye(n); b*b', -A],1,'largestreal');  x = y(n+1:2*n) / (b'*y(1:n));  or x = sign(b'*y(1:n)) * y(n+1:2*n) / norm(y(n+1:2*n));
Julia	E = eigs([-A I(n) ; b*b' -A ], nev=1 , which=:LR ) y, μ = E[2][:, 1], E[1][1] x = y[n+1:2n] ./ (b' * y[1:n]) or x = sign.(b' * y[1:n]) .* y[n+1:2n] / norm(y[n+1:2*n])
Python	M = np.block([[-A, np.eye(n)], [np.outer(b,b), -A]]) mu, y = scipy.sparse.linalg.eigs(M, k=1, which='LR', return_eigenvectors=True) x = y[n:2*n]/(np.dot(b,y[:n]))  or x = np.sign(np.dot(b,y[:n]))*y[n:2*n]/np.linalg.norm(y[n:2*n])

Symmetric generalized eigenproblems. If you prefer symmetric matrices, one can obtain a similar result with the generalized eigenvector of the two matrices $$\left( \begin{array}{cc} \!I\!\! & \!\!-A\! \\ \!-A\!\! & \! bb^\top\! \end{array} \right) \ \mbox{ and } \ \left( \begin{array}{cc} \! 0 \! & \! \! I \\[-.1cm] I \!\! & \!\! 0 \end{array} \right).$$ If you want to avoid forming a potentially dense matrix \(bb^\top\), you and use instead the matrices $$\left( \begin{array}{ccc} \!-1\! & \! 0\! & \! b^\top \! \\[-1.cm] \!0\! &\! I \!&\! -A \! \\[-.1cm]\! b \!&\! -A \!& \!0\! \end{array} \right) \ \mbox{ and } \ \left( \begin{array}{ccc} \! 0\! &\! 0 \!& \! 0\! \\[-.1cm]\! 0 \! & \! 0 \!&\! I \! \\[-.1cm] \! 0 \! &\! I \! &\! 0 \! \end{array} \right).$$ See all details in [14]. Note that beyond the two-line code above that lead to precise solutions, more efficient algorithms exist that lead to approximate solutions [14, 15].

Conclusion

In this blog post, I described one of the few non-convex problems where strong duality holds. There are many other instances within combinatorial optimization (that is, with variables in \(\{0,1\}^n\) or \(\{-1,1\}^n\)), in particular related to submodularity. I will hopefully cover these in future posts.

Acknowledgements. I would like to thank Alessandro Rudi, Gaspard Beugnot, and ChatGPT for helping with the code snippets.

References

[2] George E. Forsythe, and Gene H. Golub. On the stationary values of a second-degree polynomial on the unit sphere. Journal of the Society for Industrial and Applied Mathematics, 13(4): 1050-1068, 1965.[3] Walter Gander, Gene H. Golub, and Urs Von Matt. A constrained eigenvalue problem. Linear Algebra and its applications 114: 815-839, 1989.
[4] Andrew R. Conn, Nicholas I. M. Gould, and Philippe L. Toint. Trust region methods. Society for Industrial and Applied Mathematics, 2000.
[5] William W. Hager. Minimizing a quadratic over a sphere. SIAM Journal on Optimization, 12(1):188-208, 2001.
[6] Danny C. Sorensen. Newton’s method with a model trust region modification. SIAM Journal on Numerical Analysis, 19(2):409-426, 1982.
[7] Danny C. Sorensen. Minimization of a large-scale quadratic function subject to a spherical constraint. SIAM Journal on Optimization, 7(1):141-161, 1997.
[8] James R. Bunch, Christopher P. Nielsen, Danny C. Sorensen. Rank-one modification of the symmetric eigenproblem. Numerische Mathematik, 31(1):31-48, 1978.
[9] Ming Gu, Stanley C. Eisenstat. A stable and efficient algorithm for the rank-one modification of the symmetric eigenproblem. SIAM Journal on Matrix Analysis and Applications ,15(4):1266-1276, 1994.
[10] Imre Pólik, Tamás Terlaky. A survey of the S-lemma. SIAM Review, 49(3):371-418, 2007.
[11] Stephen P. Boyd, Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004.
[12] Franz Rendl, Henry Wolkowicz. A semidefinite framework for trust region subproblems with applications to large scale minimization. Mathematical Programming, 77(1):273-299, 1997.
[13] Satoru Adachi, Satoru Iwata, Yuji Nakatsukasa, Akiko Takeda. Solving the trust-region subproblem by a generalized eigenvalue problem. SIAM Journal on Optimization, 27(1):269-291, 2017.
[14] Elad Hazan, Tomer Koren. A linear-time algorithm for trust region problems. Mathematical Programming, 158(1-2):363-381, 2016.
[15] Amir Beck, Yakov Vaisbourd. Globally solving the trust region subproblem using simple first-order methods. SIAM Journal on Optimization, 28(3):1951-1967, 2018.

Having fun with affine constraints

Let’s now look at the solution! The second relaxation is tight, while the first is not. To prove that we have a non-tight solution for the first relaxation, we can simply find a counter-example from random matrices in dimension \(n = 2\). For example, for $$A = \left( \begin{array}{cc} \!3\! &\! 0\! \\[-.1cm] \! 0\! & \!-2 \! \end{array} \right) , \ \ b = \left( \begin{array}{c} \! 0\! \\[-.1cm] \!-1 \! \end{array} \right), \mbox{ and } \ c = \left( \begin{array}{c} \! 0\! \\[-.1cm] \!2 \! \end{array} \right),$$ a minimizer is \( x = \left( \begin{array}{c}\! \sqrt{3}/2\! \\[-.1cm] \! 1/2 \! \end{array} \right)\), with optimal value \(11/8\), while the non-tight relaxation leads to a value of \(-1/2\).

To show the tightness of the second relaxation, we first notice that the convex problem is equivalent to the following SDP relaxation: $$\min_{ X, x} \frac{1}{2} {\rm tr}(AX)-b^\top x \mbox{ such that } \left( \begin{array}{cc} \!X\!\! & \!x\! \\[-.1cm] \!x^\top \!\!&\! 1\! \end{array} \right) \succcurlyeq 0, {\rm tr}(X)=1, \mbox{ and } {\rm tr}(cc^\top X)\, – 2 t c^\top x + t^2 = 0. $$ Given the PSD constraint and the fact that $${\rm tr}(cc^\top X)\, – 2 t c^\top x + t^2 = {\rm tr} \left( \begin{array}{cc} \!X\!\! & \!x\! \\[-.1cm] \!x^\top \!\!&\! 1\! \end{array} \right)\left( \begin{array}{cc} \! cc^\top \! & \! -tc \! \\[-.1cm] \!-tc^\top \! & \! t^2 \! \end{array} \right),$$ the new constraint implies that $$ \left( \begin{array}{cc} \!X\!\! & \!x\! \\[-.1cm] \!x^\top \!\!&\! 1\! \end{array} \right) \left( \begin{array}{c} \!c\! \\[-.1cm] \!-t \! \end{array} \right)= 0, $$ that is, \(Xc = t x\) and \(c^\top x = t\). One can then check that these constraints are exactly equivalent to a projection of the problem in to a space of dimension \(n-1\). The incorrect relaxation only has \(c^\top x = t\), which is not enough. It took me a while to realize it…