Optimization is as hard as approximation

Optimization is a key tool in machine learning, where the goal is to achieve the best possible objective function value in a minimum amount of time. Obtaining any form of global guarantees can usually be done with convex objective functions, or with special cases such as risk minimization with one-hidden over-parameterized layer neural networks (see the June post). In this post, I will consider low-dimensional problems (imagine 10 or 20), with no constraint on running time (thus get ready for some running-times that are exponential in dimension!).

We consider minimizing a function \(f\) on a bounded subset \(\mathcal{X}\) of \(\mathbb{R}^d\), based only on function evaluations, a problem often referred to as zero-th order optimization or derivative-free optimization. No convexity is assumed, so we should not expect fast rates, and, again, no efficient algorithms that can provably find a global minimizer. Good references on what I am going to cover in this post are [1, 2, 5].

One may wonder why this is interesting at all. Clearly, such algorithms are not made to be used to find millions of parameters for logistic regression or neural networks, but they are often used for hyperparameter tuning (regularization parameters, size of neural network layer, etc.). See, e.g., [6] for applications.

We are going to assume some regularity for the functions we want to minimize, typically bounded derivatives. We will thus assume that \(f \in \mathcal{F}\), for a space \(\mathcal{F}\) of functions from \(\mathcal{X}\) to \(\mathbb{R}\). We are going to take a worst-case approach, where we characterize convergence over all members of \(\mathcal{F}\). That is, we want our guarantees to hold for all functions in \(\mathcal{F}\). Note that this worst-case analysis may not predict well what’s happening for a particular function; in particular, it is (by design) pessimistic.

An algorithm \(\mathcal{O}\) will be characterized by (a) the choice of points \(x_1,\dots,x_n \in \mathcal{X}\) to query the function, and (b) the algorithm to output a candidate \(\hat{x} \in \mathcal{X}\) such that \(f(\hat{x}) \ – \inf_{x \in \mathcal{X}} f(x) \) is small. The estimate \(\hat{x}\) can only depend on \((x_i,f(x_i))\), for \(i \in \{1,\dots,n\}\). In most of this post, the choice of points \(x_1,\dots,x_n\) is made once (without seeing any function values). We show later in this blog post that going adaptive, where the point \(x_{i+1}\) is selected after seeing \((x_j,f(x_j))\) for all \(j \leqslant i\), does not bring much (at least in the worst-case sense).

Given a selection of points and the algorithm \(\mathcal{O}\), the rate of convergence is the supremum over all functions \(f \in \mathcal{F}\) of the error \(f(\hat{x}) \ – \inf_{x \in \mathcal{X}} f(x)\). This is a function \(\varepsilon_n(\mathcal{O})\) of the number \(n\) of sampled points (and of the the class of functions \(\mathcal{F}\)). The optimal algorithm (minimizing \(\varepsilon_n(\mathcal{O})\)) will lead to a rate we denote \(\varepsilon_n^{\rm opt}\), and which we aim to characterize.

Direct lower/upper bounds for Lipschitz-continuous functions

The argument is particularly simple for a bounded metric space \(\mathcal{X}\) with distance \(d\), and \(\mathcal{F}\) the class of \(L\)-Lipschitz-continuous functions, that is, such that for all \(x,x’ \in \mathcal{X}\), \(|f(x) -f(x’)| \leqslant L d(x,x’)\). This is a very large set of functions, so expect weak convergence rates.

Set covers. We will need to cover the set \(\mathcal{X}\) with balls of a given radius. The minimal radius \(r\) of a cover of \(\mathcal{X}\) by \(n\) balls of radius \(r\) is denoted \(r_n(\mathcal{X},d)\). This corresponds to \(n\) ball centers \(x_1,\dots,x_n\). See example below for the unit cube \(\mathcal{X} = [0,1]^2\) and the metric obtained from the \(\ell_\infty\)-norm, with \(n = 16\), and \(r_n([0,1]^2,\ell_\infty) = 1/8\). See more details on covering numbers here.

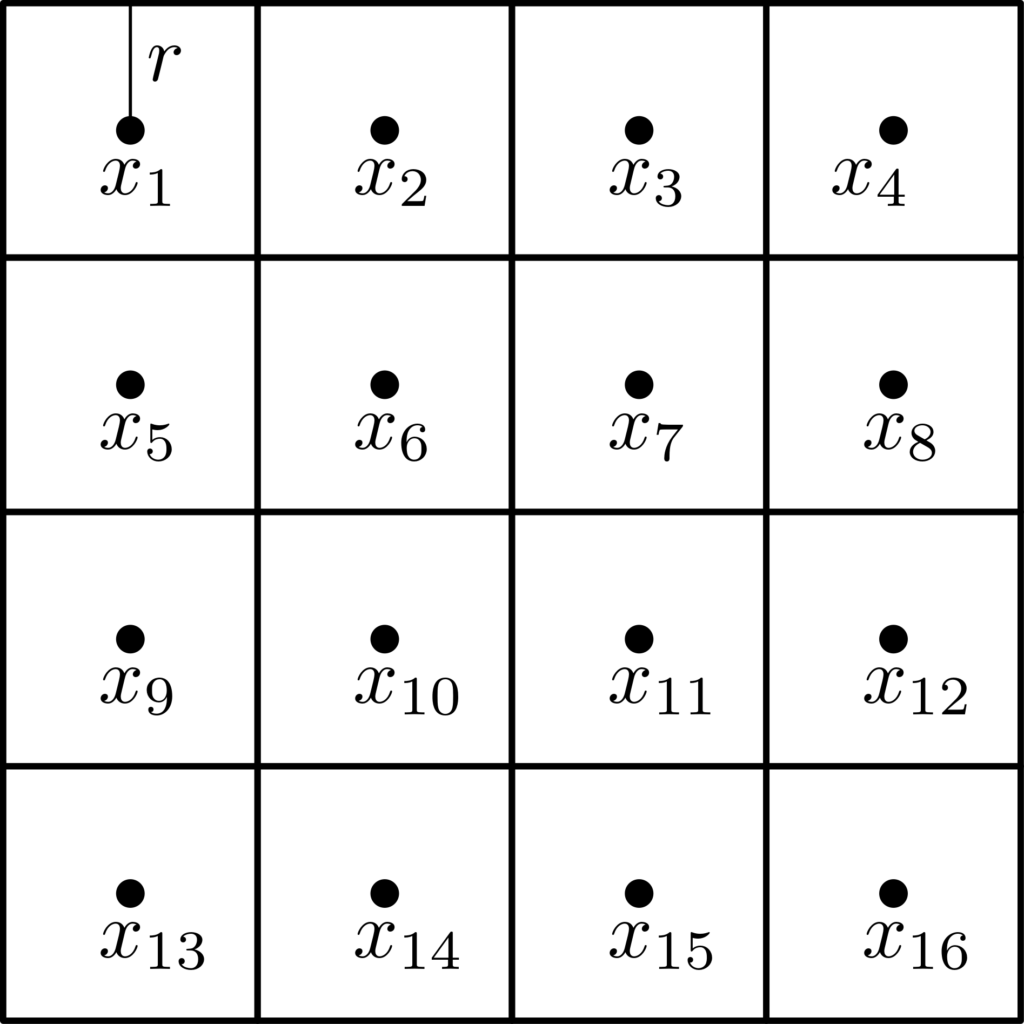
More generally, for the unit cube \(\mathcal{X} = [0,1]^d\), we have \(r_n([0,1]^d,\ell_\infty) \approx \frac{1}{2} n^{-1/d}\) (which is not an approximation where \(n\) is the \(d\)-th power of an integer). For other normed metrics, (since all norms are equivalent) the scaling as \(r_n \sim {\rm diam} (\mathcal{X}) n^{-1/d}\) is the same on any bounded set in \(\mathbb{R}^d\) (with an extra constant that depends on \(d\)).

Algorithm. Given the ball centers \(x_1,\dots,x_n\), outputting the minimum of function values \(f(x_i)\) for \(i=1,\dots,n\), leads to an error which is less than \(L r_n(\mathcal{X},d)\), as the optimal \(x_\ast \in \mathcal{X}\) is at most at distance \(r_n(\mathcal{X},d)\) from one of the cluster centers, let’s say \(x_k\), and thus \(f(x_k)\ – f(x_\ast) \leqslant L d(x_k,x_\ast) \leqslant L r_n(\mathcal{X},d)\). This provides an upper-bound on \(\varepsilon_n^{\rm opt}\). The algorithm we just described seems naive, but it turns out to be optimal for this class of problems.

Lower-bound. Consider any optimization algorithm, with its first \(n\) point queries and its estimate \(\hat{x}\). By considering the functions which are zero in these \(n+1\) points, the algorithm outputs zero. We now simply need to construct a function \(f \in \mathcal{F}\) such that \(f\) is zero at these points, but maximally smaller than zero at a different point.

[corrected June 14, 2021] Given the \(n+1\) above, there is at least a point \(y \in \mathcal{X}\) which is at distance at most \(r_{n+1}(\mathcal{X},d)\) from all of them (otherwise, we obtain a cover of \(\mathcal{X}\) with \(n+1\) points). We can then construct the function $$ f(x) = \ – L \big( r_{n+1}(\mathcal{X},d) \ – d(x,y) \big)_+ = \ – L \max \big\{ r_{n+1}(\mathcal{X},d) \ – d(x,y) ,0 \big\}, $$ which is zero on all points of the algorithm and the output point \(\hat{x}\), and with minimum value \(– L r_{n+1}(\mathcal{X},d)\) attained at \(y\). Thus, we must have \(\varepsilon_n^{\rm opt} \geqslant 0 \ – (\ – L r_{n+1}(\mathcal{X},d) ) = L r_{n+1}(\mathcal{X},d)\). This difficult function is plotted below in one dimension.

Thus, the performance of any algorithm from \(n\) function values has to be larger than \(L r_{n+1}(\mathcal{X},d)\). Thus, so far, we have shown that $$L r_{n+1}(\mathcal{X},d) \leqslant \varepsilon_n^{\rm opt} \leqslant L r_{n}(\mathcal{X},d).$$ For \(\mathcal{X} \subset \mathbb{R}^d\), \(r_n(\mathcal{X},d)\) is typically of order \({\rm diam}(\mathcal{X}) n^{-1/d}\), and thus the difference between \(n\) and \(n+1\) above is negligible. Note that the rate in \(n^{-1/d}\) is very slow, and symptomatic of the classical curse of dimensionality. The appearance of a covering number is not totally random here, as we will see below.

Random search. We can have a similar bound up to logarithmic terms for random search, that is, after selecting independently \(n\) points \(x_1,\dots,x_n\), uniformly at random in \(\mathcal{X}\), and selecting the points with smallest function value \(f(x_i)\). The performance can be shown to be proportional to \(L {\rm diam}(\mathcal{X}) ( \log n )^{1/d} n^{-1/d}\) in high probability, leading to an extra logarithmic term (the proof can be obtained with a simple covering argument, as shown at the end of the post). Therefore, random search is optimal up to logarithmic terms for this very large class of functions to optimize.

We would like to go beyond Lipschitz-continuous functions, and study if we can leverage smoothness, and hopefully avoid the dependence in \(n^{-1/d}\). This can be done by a somewhat surprising equivalence between worst case guarantees from optimization and worst case guarantees for uniform approximation.

Optimization is as hard as uniform function approximation

We now also consider the problem of outputting a whole function \(\hat{f} \in \mathcal{F}\), such that \(\|f – \hat{f}\|_\infty = \max_{x \in \mathcal{X}} | \hat{f}(x)\ – f(x)|\) is as small as possible. For any approximation algorithm \(\mathcal{A}\) that builds an estimate \(\hat{f} \in \mathcal{F}\) from \(n\) function values, we can define its convergence rate in the same way as for optimization algorithm \(\varepsilon_n(\mathcal{A})\), as a function of \(n\). The optimal approximation algorithm has a convergence rate denoted by \(\varepsilon_n^{\rm app}\).

From approximation to optimization. Clearly, an approximation algorithm \(\mathcal{A}\) leads to an optimization algorithm \(\mathcal{O}\) with at most twice the same rate, that is, $$ \varepsilon_n(\mathcal{O}) \leqslant 2\varepsilon_n(\mathcal{A}),$$ by simply approximating \(f\) by \(\hat{f}\) and outputting any \(\hat{x} \in \arg \min_{x \in \mathcal{X}} \hat{f}(x)\), for which $$f(\hat{x}) \leqslant \hat{f}(\hat{x}) + \| \hat{f}\ – f\|_\infty = \min_{x \in \mathcal{X}} \hat{f}(x) + \| \hat{f}\ – f\|_\infty \leqslant \min_{x \in \mathcal{X}} {f}(x) +2 \| \hat{f} \ – f\|_\infty. $$ See an illustration below (with a function estimated from the values at green points), with the candidate minimizer in orange.

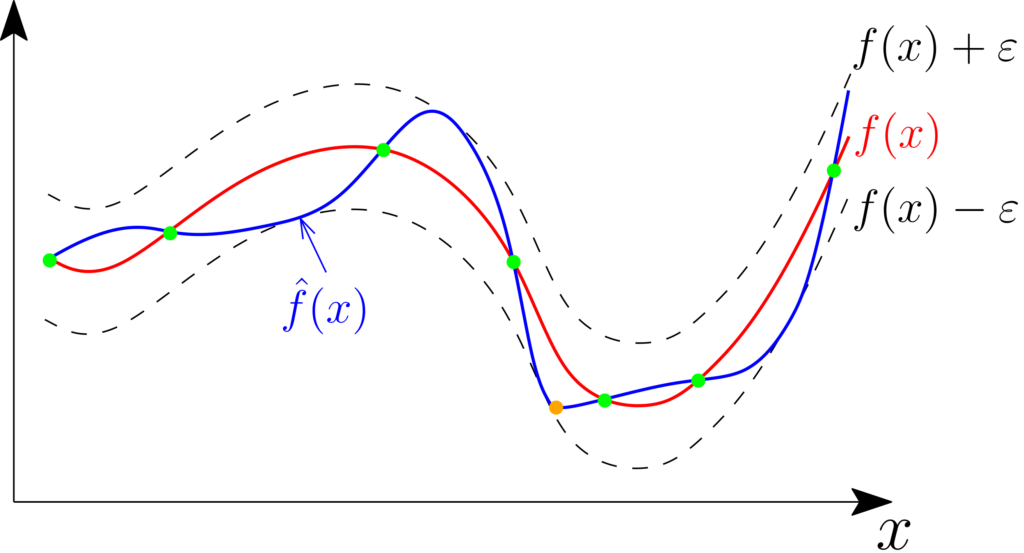
Thus in terms of worst-case performance, we get $$ \varepsilon_n^{\rm opt} \leqslant 2\varepsilon_n^{\rm app}.$$ Intuitively, it seems that this upper-bound should be very loose, as approximating uniformly a function, in particular far from its minimum, seems useless for minimization. For worst-case performance, this intuition is incorrect… Indeed, the optimal rate for optimization with \(n\) function evaluations happens to be greater than the optimal rate for approximation with \(n+1\) function evaluations, which we will now show.

Lower-bound on optimization performance. We will need an extra assumption, namely that the function space \(\mathcal{F}\) is convex and symmetric (and bounded in uniform norm).

We consider an optimization algorithm over the class of function \(\mathcal{F}\), that is considering \(n\) observation points \(x_1,\dots,x_n\), and an estimate \(\hat{x}\). The worst-case performance over all functions in \(\mathcal{F}\) is greater than over the (smaller) class of functions for which \(f(x_1) = \cdots = f(x_n) = f(\hat{x}) = 0\). Given that the performance measure is \(f(\hat{x})\ – \inf_{x \in \mathcal{X}} f(x)\), the performance is greater than the supremum of \(– \inf_{x \in \mathcal{X}} f(x)\) over functions in \(\mathcal{F}\) such that \(f(x_1) = \cdots = f(x_n) = f(\hat{x}) = 0\). For Lipschitz-continuous functions above, we built explicitly a hard function. In the general case, an explicit construction is not that easy, but we will relate the construction of such a function to the general approximation problem.

As we just saw, the optimal rate of the optimization algorithm is greater than $$\inf_{x_1,\dots,\, x_{n+1} \in \, \mathcal{X}} \sup_{f \in \mathcal{F}, \ f(x_1)\ =\ \cdots \ = \ f(x_{n+1}) \ =\ 0} – \inf_{x \in \mathcal{X}} f(x) . $$ The quantity above characterizes how small a function can be when equal to zero on \(n+1\) points. When the set of function \(\mathcal{F}\) is centrally symmetric, that is \(f \in \mathcal{F} \Rightarrow \ – f \in \mathcal{F}\), we can replace \(– \inf_{x \in \mathcal{X}} f(x)\) in the expression above by \(\| f\|_\infty\).

It turns out that for convex and centrally symmetric spaces \(\mathcal{F}\) of functions, this happens to be the optimal rate of approximation with \(n+1\) function evaluations. This is sometimes referred to as Smolyak’s lemma [3], which we state here (see a very nice and short proof in [4]).

Smolyak’s lemma. We consider a space of functions \(\mathcal{F}\) which is convex and centrally symmetric. Then:

• For any \(x_1,\dots,x_n \in \mathcal{X}\), the optimal approximation method, that is the optimal map \(\mathcal{S}: \mathbb{R}^n \to \mathcal{F}\), i.e., an algorithm that computes \(\hat{f} = \mathcal{S}(f(x_1),\dots,f(x_n)) \in \mathcal{F}\), is linear, that is, there exist functions \(g_1,\dots,g_n: \mathcal{X} \to \mathbb{R}\) such that $$\mathcal{S}(f(x_1),\dots,f(x_n)) = \sum_{i=1}^n f(x_i) g_i.$$
• The optimal rate of uniform approximation in \(\mathcal{F}\) is equal to $$ \displaystyle \varepsilon_n^{\rm app} = \inf_{x_1,\dots,\, x_{n} \in \, \mathcal{X}} \sup_{f \in \mathcal{F}, \ f(x_1)\ =\ \cdots \ = \ f(x_{n}) \ =\ 0} \| f \|_\infty.$$

Thus, we have “shown” that: $$ \varepsilon_{n+1}^{\rm app} \leqslant \varepsilon_n^{\rm opt} \leqslant 2\varepsilon_n^{\rm app}, $$ that is, optimization is at most twice as hard as uniform approximation (still in the worst-case sense). We can now consider examples of uniform approximation algorithms to get optimization algorithms.

Examples and optimal algorithms

As seen above, we simply need algorithms that approximate the function in uniform norm, and then we minimize the approximation. This is computationally optimal in terms of access to function evaluations (but clearly not in terms of computational complexity).

Lipschitz-continuous functions. One can check that with \(x_1,\dots,x_n\) the centers of the cover above, and a piecewise constant function on each of the ball (with arbitrary values at intersections), then we have $$ \| \hat{f} \, – f \|_\infty \leqslant L r_n(\mathcal{X},d),$$ which is a standard approximation result using covering numbers. We recover the result above directly from the cover argument (and here the sharper result that the rates of uniform approximation and optimization are asymptotically the same for this class of functions).

Smooth functions in one dimension. For simplicity, I will focus on the one-dimensional problem, where all concepts are simpler, some of them directly extend to higher dimensions, some of them don’t.

We consider \(\mathcal{X} = [0,1]\). The simplest interpolation techniques are piecewise constant and piecewise affine interpolations. That is, if we observe \(0 = x_1 \leqslant \cdots \leqslant x_n = 1\), we consider \(\hat{f}\) defined on \([x_i,x_{i+1}]\) as $$\hat{f}(x) = \frac{1}{2}f(x_i) + \frac{1}{2}f(x_{i+1}) $$

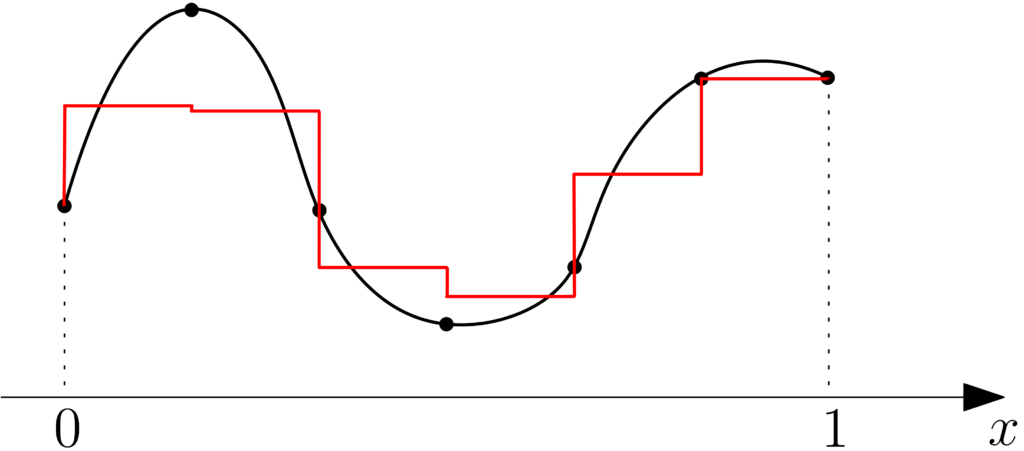
or $$ \hat{f}(x) = f(x_i) + \frac{ x\ – x_i}{x_{i+1}-x_i}\big[ f(x_{i+1})\ – f(x_i) \big].$$

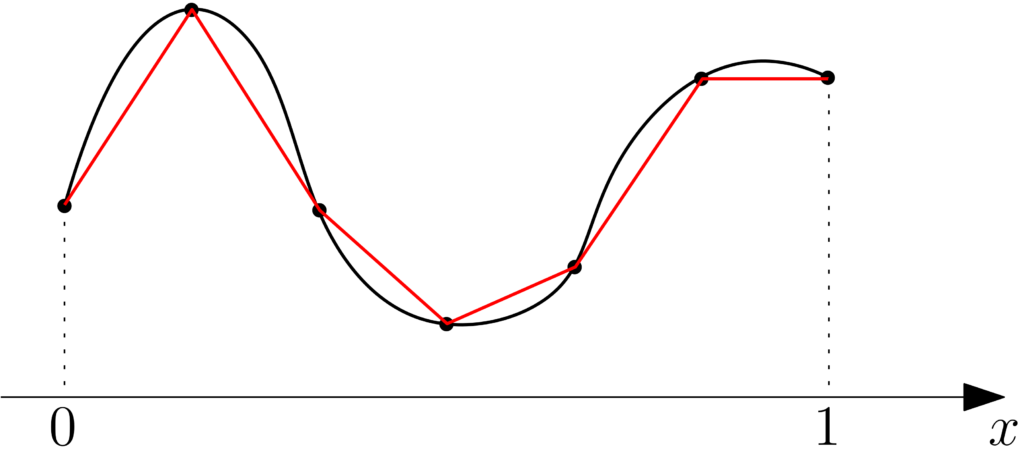
If we assume that \(f\) is twice differentiable with second-derivative bounded by \(M_2\), then, we can show that on \([x_i,x_{i+1}]\), we have for piecewise affine interpolation: $$ | f(x) \ – \hat{f}(x) | \leqslant \frac{M_2}{8} | x_{i+1} – x_i |^2.$$

If we assume that \(f\) is differentiable with first-derivative bounded by \(M_1\), then, we can show that on \([x_i,x_{i+1}]\), we have for piecewise affine or constant interpolation: $$ | f(x) \ – \hat{f}(x) | \leqslant \frac{M_1}{2} | x_{i+1} – x_i |.$$

This leads to, when \(x_i = (i-1)/(n-1)\), to uniform error in \(O(1/n)\) for functions with a bound on a single derivative and or \(O(1/n^2)\) for two derivatives. Thus, we see two effects, that are common in approximations problems: (a) the more regular the function to approximate, the better the approximation rate, (b) If we consider a method tailored to smoother functions, it often works well for less smooth functions.

Explicit piecewise affine interpolation is harder to perform in higher dimensions, where other techniques can be used as presented below, such as kernel methods (again!).

Going high-dimensional with kernel methods. We assume that we have a positive definite kernel \(k: \mathcal{X} \times \mathcal{X} \to \mathbb{R}\) on \(\mathcal{X}\), and, given the \(n\) elements \(x_1,\dots,x_n\) of \(\mathcal{X}\) and function values \(f(x_1),\dots,f(x_n)\), we look for the interpolating function \(f\) in the corresponding reproducing kernel Hilbert space with minimum norm. By the representer theorem, it has to be of the form \(\sum_{i=1}^n \alpha_i k(x,x_i)\). Since it has to interpolate, we must have \(K\alpha = y\) and thus \(\alpha = K^{-1} y\), where \(y_i = f(x_i)\) for \(i \in \{1,\dots,n\}\), and \(K\) the \(n \times n\) kernel matrix. Thus, interpolation can then be easily done in higher dimensions.

Sobolev spaces are commonly used in the interpolation context, and for \(s\) square-integrable derivatives, for \(s > d/2\), they are reproducing kernel Hilbert spaces. See below for examples of interpolations with various Sobolev spaces and increasing number of interpolating points, where the approximation errors (in uniform norm) are computed. With \(s=1\), we recover piecewise affine interpolation, but smoother functions are obtained for \(s=2\).

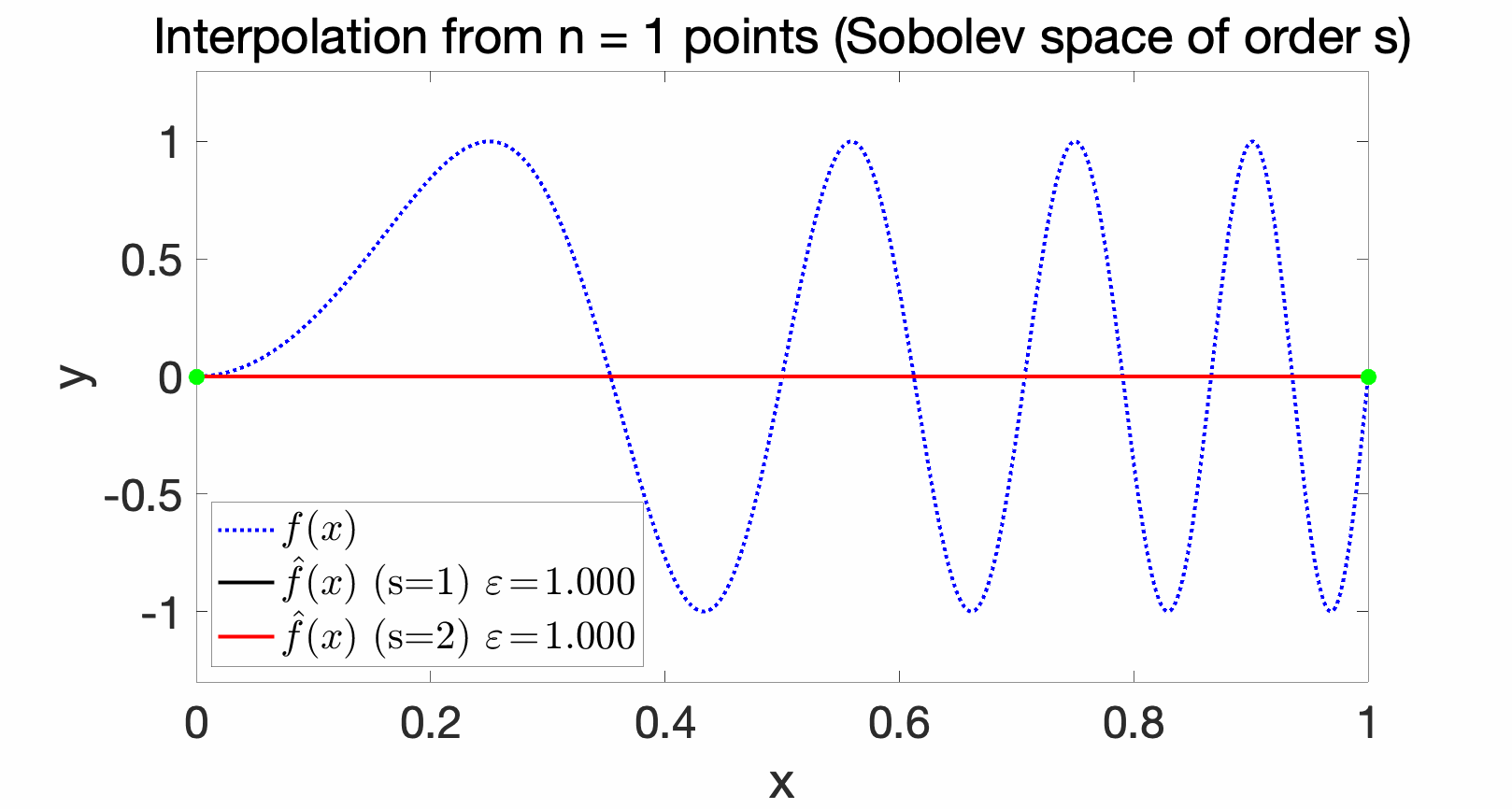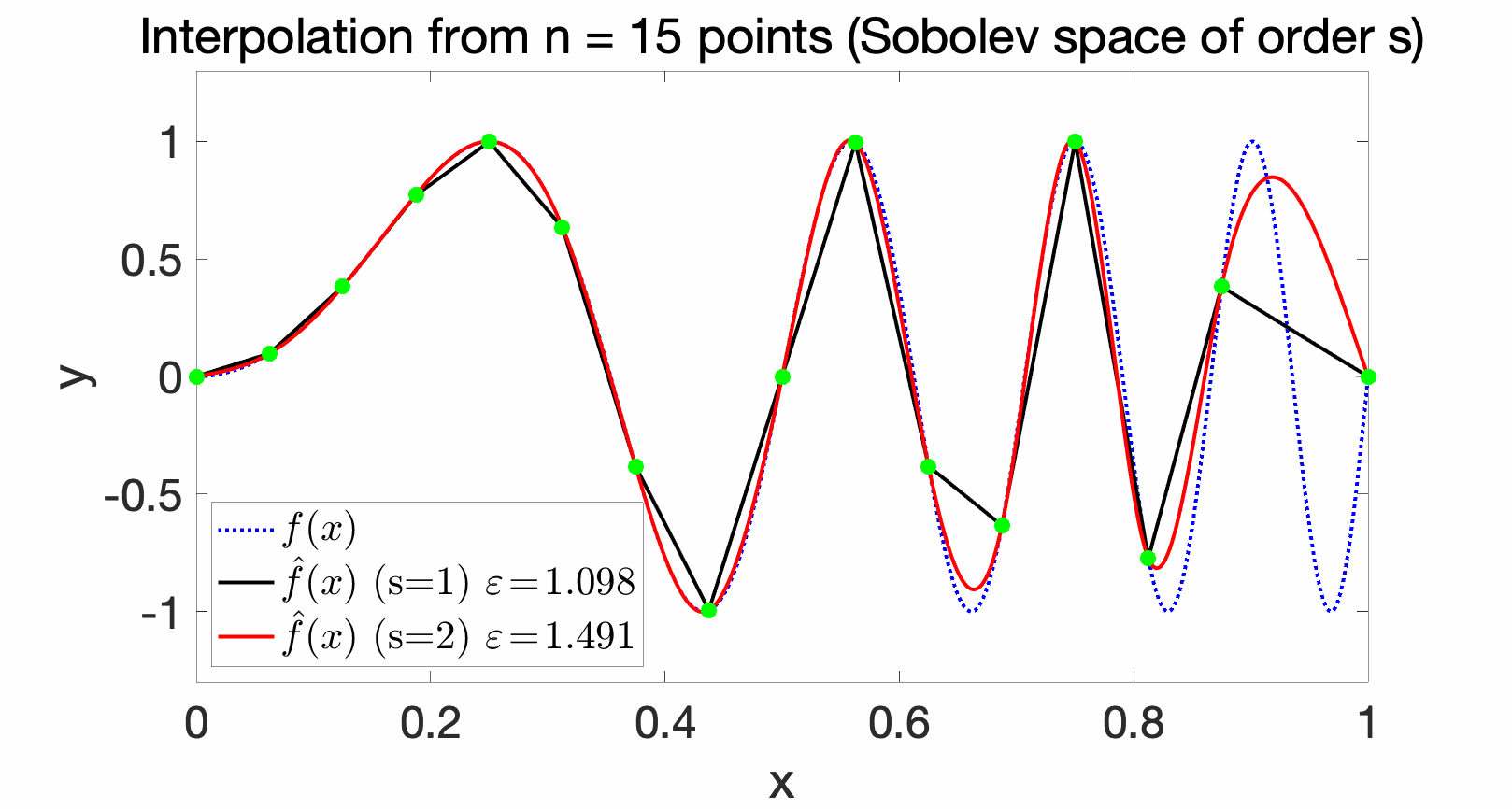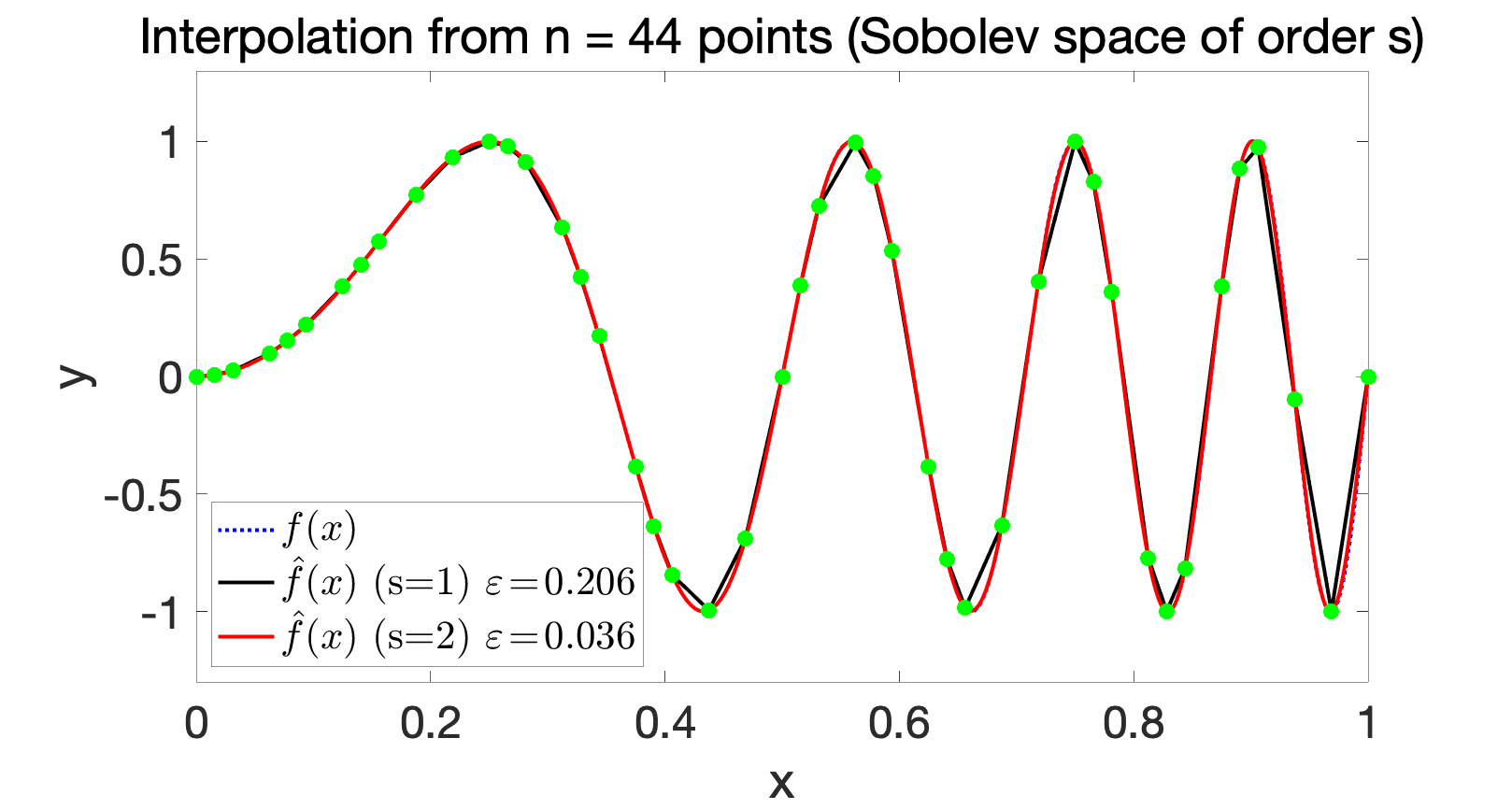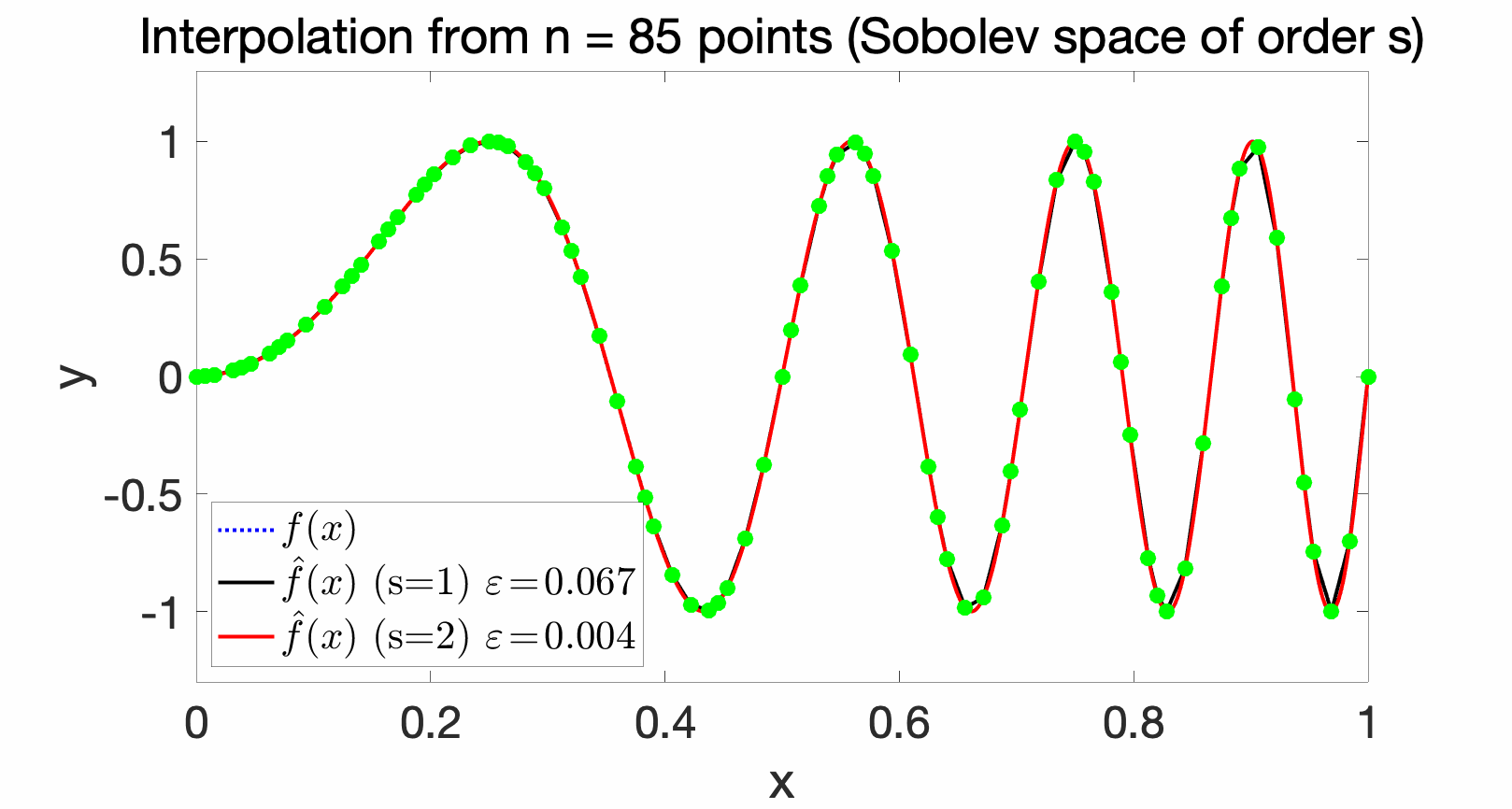
Optimal rates of approximation. With the method defined above, we can obtain the optimal rates of approximation (and hence of optimization) of \(\varepsilon_n^{\rm app} \approx \displaystyle \frac{1}{n^{m/d}}\), for the set of functions with \(m\) bounded derivatives. Thus, for very smooth functions, we can escape the curse of dimensionality (that is, obtain a power of \(n\) that does not decay too slowly). See [1] for more details.

The powerlessness of adaptivity

The critical reader may argue that the algorithm set-up described in this post is too simple: the points at which we take function values are decided once and for all, independently of the observed function values. Clearly, some form of adaptivity should beat random search. The sad truth is that the bound for worst-case performance is the same… up to a factor of 2 at most (still in the worst-case sense).

The argument is essentially the same as for non-adaptive algorithms: for the Lipschitz-continuous example, our hard function can also be built for adaptive algorithms, while for the general case, it simply turns out that the rate for adaptive approximation is exactly the same than for adaptive approximation [4].

Thus, adaptive and non-adaptive approximations are just a factor of two of each other. Note that given the practical success of Bayesian optimization (which is one instance of adaptive optimization) on some problems, there could be at least two explanations (choose the one you prefer, or find a new one): (1) the worst-case analysis can be too pessimistic, or (2) what is crucial in Bayesian optimization is not the adaptive choice of points to evaluate the function, but the adaptivity to smoothness of the function to optimize (that is, if the function has \(m\) derivatives, then the rate is \(n^{-m/d}\), which can be much better than \(n^{-1/d}\)).

Conclusion

In this post, I highlighted the strong links between approximation problems and optimization problems. It turns out that the parallel between worst-case performances goes beyond: computing integrals from function evaluations, a problem typically referred to as quadrature, is also as hard. More on this in a future post.

As warned early in the post, the algorithms presented here all have running time that are exponential in dimension, as they either perform random sampling or need to minimize a model of the function to optimize.

The only good news in this post: optimization is hard as approximation, but the scenario is more varied than expected. Indeed approximation can be fast and avoid the curse of dimensionality, at least in the exponent of the rate, when the function is very smooth (indeed, for \(m\)-times differentiable functions, the constant in front of \(n^{-m/d}\) still depends exponentially in \(d\)). It would be nice to catch this property also in an optimization algorithm, with a running time complexity depending polynomially on \(n\) only, and not exponentially in \(d\). Next month, I will present recent work with Alessandro Rudi and Ulysse Marteau-Ferey [7] that does exactly this, by combining the tasks of interpolation and optimization in a single convex optimization problem.

Acknowledgements. I would like to thank Alessandro Rudi and Ulysse Marteau-Ferey for proofreading this blog post and making good clarifying suggestions.

References

[1] Erich Novak. Deterministic and stochastic error bounds in numerical analysis. Springer, 2006.
[2] Erich Novak, Henryk Woźniakowski. Tractability of Multivariate Problems: Standard information for functionals, European Mathematical Society, 2008.
[3] S. A. Smolyak. On optimal restoration of functions and functionals of them, Candidate Dissertation, Moscow State University, 1965.
[4] Nikolai Sergeevich Bakhvalov. On the optimality of linear methods for operator approximation in convex classes of functions. USSR Computational Mathematics and Mathematical Physics. 11(4): 244-249, 1971.
[5] Yurii Nesterov. Lectures on Convex Optimization. Springer, 2018.
[6] Jasper Snoek, Hugo Larochelle, and Ryan P. Adams. Practical Bayesian optimization of machine learning algorithms. Advances in Neural Information Processing Systems, 2015.
[7] Alessandro Rudi, Ulysse Marteau-Ferey, Francis Bach. Finding Global Minima via Kernel Approximations. Technical report arXiv 2012.11978, 2020.

Performance of random search

We consider sampling independently and uniformly in \(\mathcal{X}\) \(n\) points \(x_1,\dots,x_n\). For a given \(L\)-Lipschitz-continuous function \(f\), with global minimizer \(x\) on \(\mathcal{X}\), we have $$\min_{i \in \{1,\dots,n\}} f(x_i)\ – f(x) \leqslant L \min_{i \in \{1,\dots,n\}} d(x,x_i).$$ Thus, to obtain an upper-bound on performance over all functions \(f\) (and potentially all locations of the global minimizer \(x\)), we need to bound $$\max_{x \in \mathcal{X}} \min_{i \in \{1,\dots,n\}} d(x,x_i).$$ If we have a cover with \(m\) points \(y_1,\dots,y_m\), and radius \(r = r_m(\mathcal{X},d)\), we have $$\max_{x \in \mathcal{X}} \min_{i \in \{1,\dots,n\}} d(x,x_i) \leqslant r + \max_{j \in \{1,\dots,m\}} \min_{i \in \{1,\dots,n\}} d(y_j,x_i) .$$ We can then bound the probability that $$ \max_{j \in \{1,\dots,m\}} \min_{i \in \{1,\dots,n\}} d(y_j,x_i) \geqslant r$$ by the union bound (and using the independence of the \(x_i\)’s) as \(m\) times the \(n\)-th power of the probability that one of the \(x_i\) is not in a given ball of radius \(r\). By a simple volume argument (and assuming that all balls of a given radius have the same volume), this probability is less than \(( 1 – 1/m)\). Thus with probability greater than \(1 – m(1 – 1/m)^n \geqslant 1 – m e^{ – n /m}\) the worst-case performance is less than \(2Lr\).

Since for normed metrics in \(\mathbb{R}^d\), \(r \sim m^{-1/d} {\rm diam}(\mathcal{X})\), by selecting \(m = 2n \log n\), we get an overall performance proportional to \( L \big( \frac{ \log n}{n} \big)^{1/d}\) with probability greater than \(1 – \frac{ \log n}{n}\) (which tends to one when \(n\) grows).