Scaling laws of optimization

Scaling laws have been one of the key achievements of theoretical analysis in various fields of applied mathematics and computer science, answering the following key question: How fast does my method or my algorithm converge as a function of (potentially partially) observable problem parameters.

For supervised machine learning and statistics, probably the simplest and oldest of all such scaling laws is the classical rate \(\sigma^2 d / n\) for ordinary least-squares (where \(d\) is the number of features, \(n\) the number of observations, and \(\sigma^2\) the noise variance). This has been extended over the years in the statistics community for various non-linear function estimation, with excess risks for regression essentially proportional to \(n^{-2s/(2s+d)}\), where \(s\) is now the order of derivatives that exist for the optimal prediction function (see, e.g., these two nice books [1, 2]). Such scaling laws also have a long history in the part of statistical physics that looks into high-dimensional statistical estimation problems (see, e.g., [3]), as well in random matrix theory (see, e.g., [4, 28]). Note that a particular feature of a theoretical scaling law is that it should be an asymptotic equivalent rather than an upper bound, which is the traditional set up in learning theory (and for good reasons, see, e.g., my soon to be published book [5]).

While there is a long history of scaling laws in theoretical circles, empirical variants have recently emerged for large-scale neural networks [26, 27], where new quantities (such as the amount of computing power available) have appeared. Here, the algorithm is run with several values of the problem parameters, and a parameterized scaling law is fit to the empirical performance, with the hope of predicting performance outcomes in future experiments. See a comprehensive summary here.

In this blog post, I want to tackle the following question: are there standard scaling laws for optimization with (stochastic) gradient descent? In other words, how many iterations should I really expect as a function of simple problem parameters?

As for scaling laws for predictive performance, answers have to be dedicated to a specific class of problems. In this post, I will focus on the simplest possible set-up: unconstrained convex quadratic optimization problems. Why?

• Because the analysis can be made asymptotic without too much effort using linear algebra (convex optimization problems classically leads to upper bounds on performance, as covered in an earlier blog post, but not typically to simple equivalents).
• Many of the concepts in convex optimization are often seen (at least locally) in this class of functions. Clearly, other posts are needed to go beyond. Even more, I will focus on deterministic gradient descent in this post, showing in a future post how this extends to the stochastic version (I will also briefly mention accelerated gradient descent).

What does classical optimization theory say?

We consider a convex quadratic function \(F: \mathbb{R}^d \to \mathbb{R}\). If we assume that it is lower-bounded, then it has a minimizer \(\theta_\ast\), and a minimal value, denoted \(F_\ast\). If \(H \in \mathbb{R}^{d \times d}\) denotes its positive semidefinite Hessian matrix, the function \(F\) can be written as $$ F(\theta) = \frac{1}{2} ( \theta\, – \theta_\ast)^\top H ( \theta\, – \theta_\ast) + F_\ast. $$ Its gradient has the following expression $$ \tag{1} F'(\theta) = H ( \theta \, – \theta_\ast). $$

The gradient descent algorithm is then an iterative algorithm starting at some \(\theta_0 \in \mathbb{R}^d\), with the following iteration, for \(k \geqslant 1\): $$ \theta_{k} = \theta_{k-1} – \gamma F'(\theta_{k-1}).$$ We consider a constant step size \(\gamma>0\) for simplicity. Since we have a linear iteration, we have, given the expression of the gradient in \((1)\), $$ \theta_k\, – \theta_\ast = ( I – \gamma H)^k ( \theta_0 \, – \theta_\ast),$$ leading to an explicit formula for the classical performance criterion based on function values: $$ F(\theta_k)\, – F_\ast = \frac{1}{2} (\theta_0 \, – \theta_\ast)^\top H ( I- \gamma H)^{2k} (\theta_0 \, – \theta_\ast).$$

Exponential convergence. As reviewed in Section 5.2.1 of my book [5], the classical “strongly convex” analysis assumes that all eigenvalues of \(H\) are between \(\mu\) and \(L\), with \(\mu > 0\). Then, for \(\gamma \leqslant 1/L\), the matrix \(( I- \gamma H)^{2k}\) only has nonnegative eigenvalues less than $$ ( 1 \, – \gamma \mu)^{2k}, $$ and thus, for \(\gamma = 1/L\), $$ \tag{2}F(\theta_k)\, – F_\ast \leqslant \Big( 1 \, – \frac{\mu}{L}\Big)^{2k} \big[ F(\theta_0) \, – F_\ast \big].$$ We thus get exponential convergence, but with a constant \(\big(1- \frac{\mu}{L}\big)\) that goes to one if \(\mu\) is close to zero. In particular, when \(\mu = 0\), this result simply states that function values do not go up, potentially without convergence.

Rate in \(O(1/k)\). The classical “non strongly convex” analysis considers explicitly the case \(\mu =0\), and uses that the function \(\alpha \mapsto \alpha ( 1 – \alpha)^{2k}\) is maximized at \(\alpha = \frac{1}{2k+1}\) with maximal value \(\frac{1}{2k+1} \big( \frac{2k}{2k+1} \big)^{2k} \leqslant \frac{1}{2ek }\) for \(k \geqslant 1\), leading to the bound, for \(\gamma = 1/L\), $$ \tag{3}F(\theta_k) \, – F_\ast \leqslant \frac{L}{4 e}\| \theta_0 \, – \theta_\ast\|_2^2 \cdot \frac{1}{k}.$$

Why is this not good enough? The two bounds in equations \((2)\) and \((3)\) are too crude for the following reasons:

• The exponentially convergent bound in equation \((2)\) is only meaningful if the condition number \(L / \mu\) is not too large, and for modern machine learning problems, strong convexity is only obtained through a regularizer, with condition numbers that often grow up linearly in \(n\) (this corresponds to a common regularizer proportional to a constant times \(\frac{1}{n} \| \theta\|_2^2\)). Thus, the strongly convex analysis is often meaningless when doing not much more than \(n\) iterations of the algorithm.
• The rate in \(O(1/k)\) in equation \((3)\) totally misestimates the actual dependence in \(k\), as it relies on a crude bound. As shown in the examples below, it often (non surprisingly) underestimates the actual performance, but, in early iterations, it may also overestimate it (which is more surprising as it comes from an upper bound).

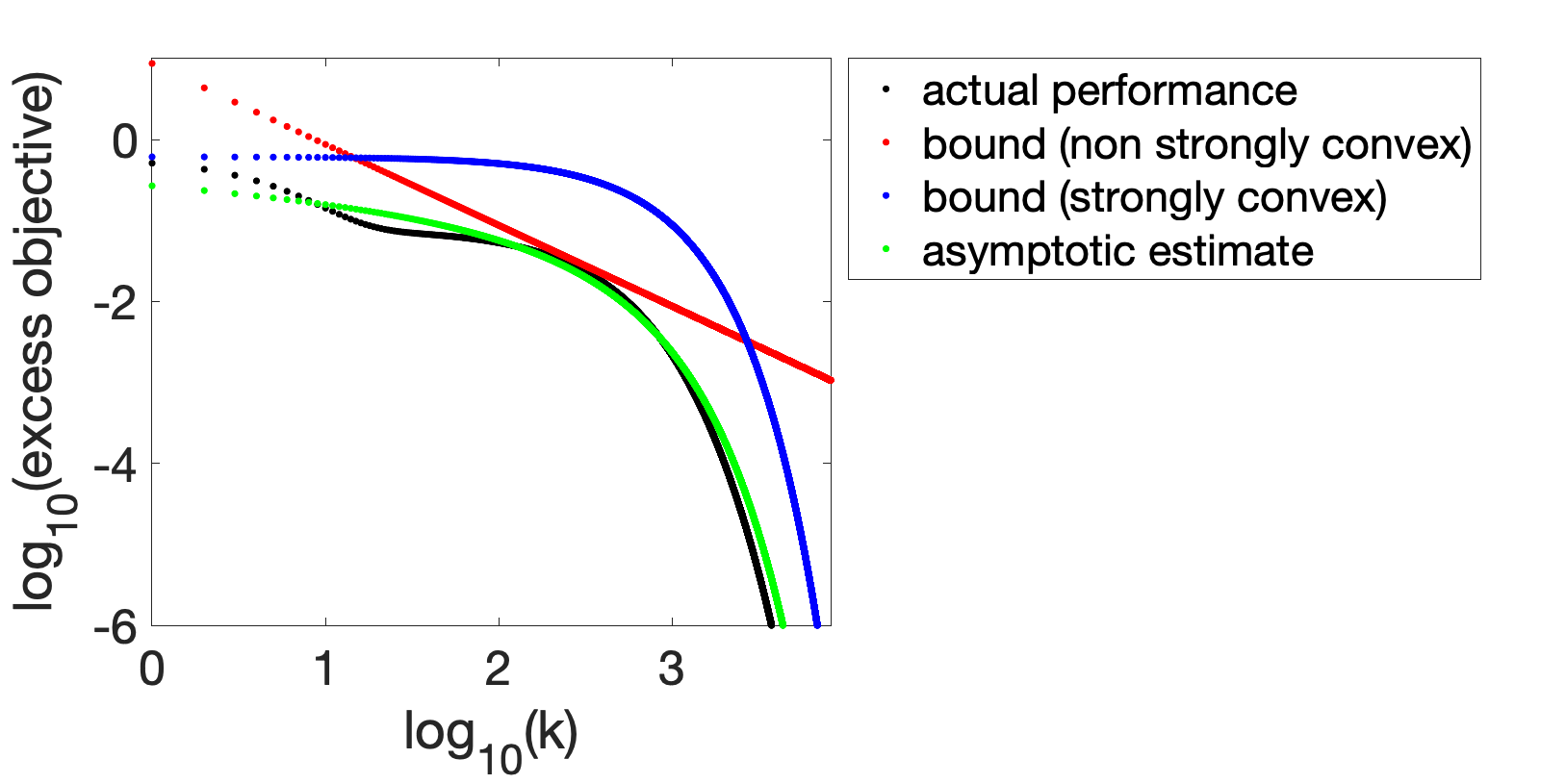
Two classical behaviors. Below, we present two examples obtained from the model we detail below, outlining two behaviors that can be expected from running gradient descent in machine learning contexts (and quadratic objective functions). The two cases correspond to small strong convexity constant \(\mu\), so that we observe lines in log-log plot (thus a convergence rate as a power of \(k\)) until a dip indicative of exponential convergence, around \(k \approx L/\mu\).

The first case corresponds to an underestimation of the non-strongly convex bound (here, the scaling law is in \(1/k^{3/2}\) in early iterations).

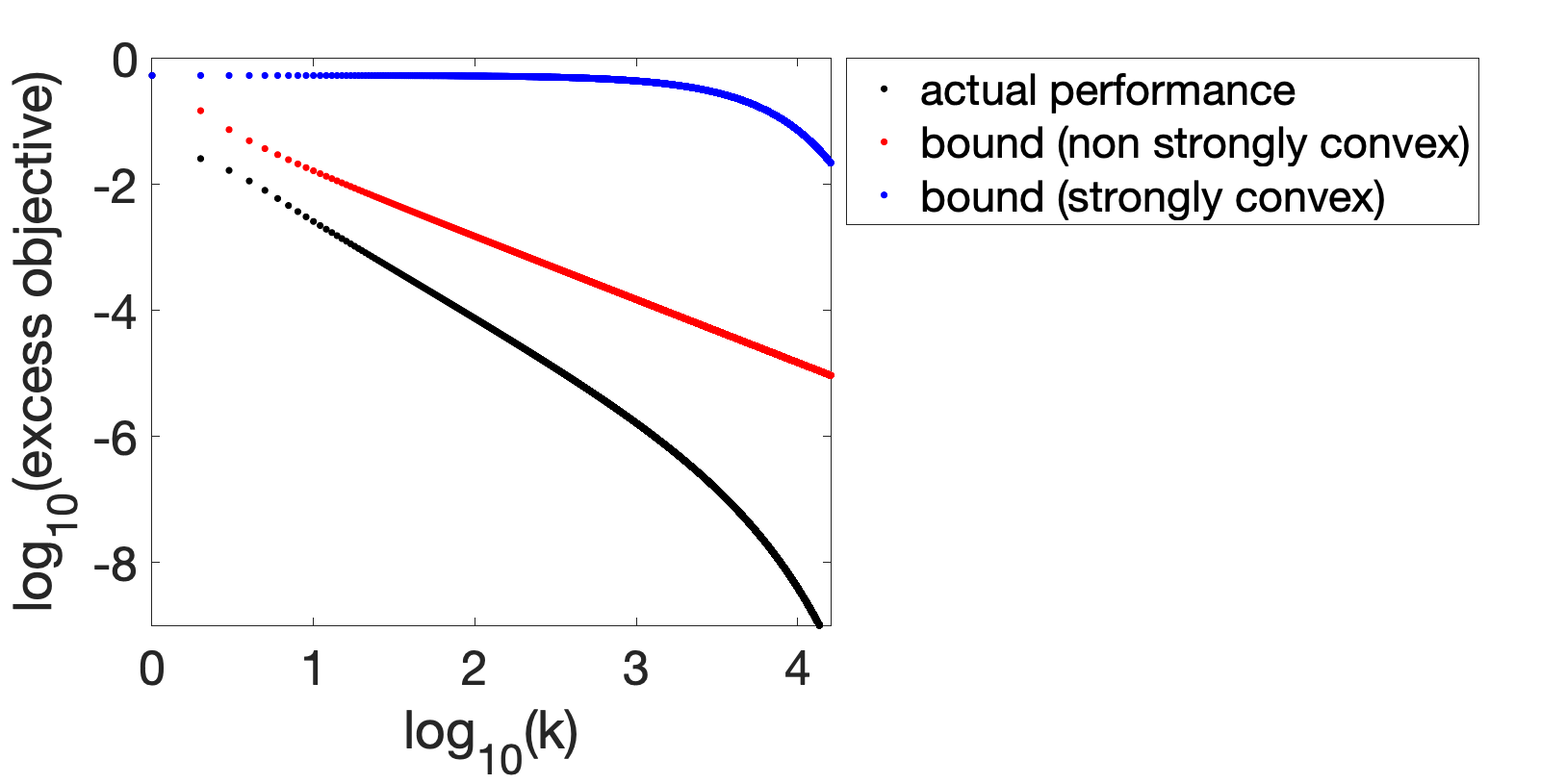
The second case corresponds to a worse situation regarding the bound: the rate \(O(1/k)\) may in fact be optimistic, as shown below (where the rate for small \(k\) is proportional to \(1/k^{1/2}\)).

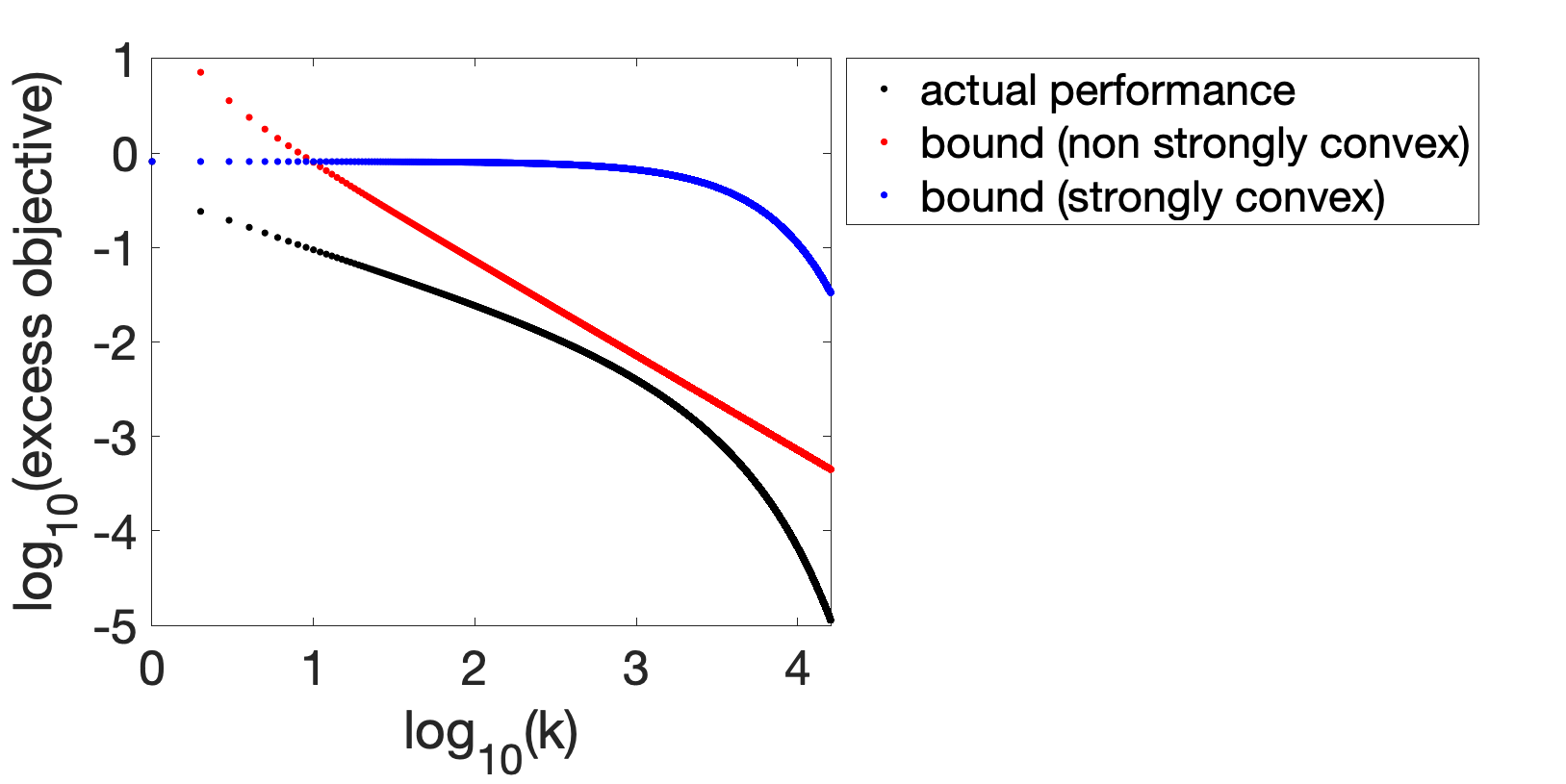
What’s happening? Since the problem is invariant by rotation, without loss of generality, for the analysis only, we can place ourselves in a basis of eigenvectors of \(H\), and thus consider $$H = {\rm Diag}(h)$$ a diagonal matrix with \(h \in \mathbb{R}^d\) the vector of non-increasing eigenvalues of \(H\). If \(\delta \in \mathbb{R}^d\) is the vector of projections of \(\theta_0 \, – \theta_\ast\) onto these eigenvectors, we obtain: $$F(\theta_k) \, – F_\ast= \frac{1}{2} \sum_{i=1}^d \delta_i^2 h_i ( 1 \, – \gamma h_i)^{2k},$$ which is a sum of exponentials.

The strongly convex bound relies on upper bounding all exponentials by the slowest one, while the non strongly convex bound relies on uniformly replacing \(\alpha ( 1 \, – \alpha)^{2k}\) by its maximal value. This is too crude, and the “correct” way to study the collective behavior of all eigenvalues is through Laplace’s method, which was studied in an earlier post. Note that a difficulty we will have to face is the presence of two different regimes: one with polynomial convergence and then one with exponential convergence.

Before doing so, we need to define a good model for the sequences \((\delta_i)_{i \geqslant 1}\) and \((h_i)_{i \geqslant 1}\).

What is a good model for machine learning problems?

Optimization is much broader than machine learning, but I’ll focus on what I know well and a model that suits well some classical machine learning optimization problems (if you have any other model which is relevant in other applications, please let me know). Other models can be considered using random matrix theory (see, e.g., [6, 16]).

In this blog post, I will consider the following asymptotic model (it does not need to be true exactly for all \(i\), just asymptotically when \(i\) tends to infinity):

• Infinite-dimensional problem, i.e., \(d = +\infty\): large-dimensional problems often require tools from infinite dimensions, and we follow this approach here.
• Eigenvalues of Hessian matrix as $$ h_i \sim \lambda + \frac{L}{i^\alpha},$$ with \(\alpha > 1\), which corresponds to a regularization by \(\frac{\lambda}{2} \| \theta\|_2^2\), on top of a decaying spectrum with finite trace (e.g., sum of eigenvalues). Here, since we have a sequence \((1/i^\alpha)_{i \geqslant 1}\) decaying to zero, the strong-convexity parameter is \(\mu = \lambda\), and we will sometimes take it as \(0\) in our analysis.
• Components of deviation to optimum: when \(\lambda =0\), we consider a polynomial decay $$ \delta_i \sim \frac{\Delta}{i^{\beta/2}}.$$ A natural assumption would be that \(\beta > 1\), so that \(\| \theta_0 \, – \theta_\ast\|_2^2\) is bounded, but we can go further. In fact, the only constraints is that \(\delta^\top H \delta\) is finite (that is, finite function value at initialization), which leads to \(\kappa = \alpha + \beta > 1\). We could keep the same model even with a regularizer (\(\lambda >0\)), but an alternative model that is equivalent for \(\lambda = 0\) but closer to machine learning examples is $$\tag{4}\delta_i \sim \frac{\Delta}{i^{\beta/2}} \cdot \frac{1}{1+ \frac{\lambda}{L} i^\alpha}.$$ This idealized model has the nice consequence to have \(\| \delta\|_2^2\) always finite for any \(\alpha + \beta > 1\) and \(\lambda > 0\), which always allows comparisons with the non-strongly convex bound obtained in \((3)\). Note that we can obtain the same asymptotic result “in probability”, if we multiply \(\delta_i\) by an independent random variable \(z_i\) with \(\mathbb{E} [ z_i^2 ] = 1\) and \(\mathbb{E} [ z_i^4 ]\) finite (as shown below, this corresponds to a random prediction function in machine learning problems).

I provide a justification why this a relevant model for machine learning later in the post, and start with the asymptotic analysis with Laplace’s method (which can be easily extended to series [7], see also [24] in the context of prediction performance).

Asymptotical analysis

Given the model defined above, we can find asymptotic equivalents, starting with the simpler case with no regularizer (\(\lambda=0\)).

Starting with \(\lambda = 0\) (no regularization). We have, with assumptions above and \(a_k = F(\theta_k) \, – F_\ast\), with \(\gamma L \leqslant 1\): $$ a_k = \frac{1}{2} \sum_{i=1}^{+\infty} \delta_i^2 h_i ( 1 \, – \gamma h_i)^{2k} = \frac{1}{2} \sum_{i=1}^{+\infty} \frac{L \Delta^2}{ i^{\beta+\alpha}} \Big( 1\, – \frac{\gamma L}{i^\alpha} \Big)^{2k}.$$

We equivalently study the integral instead of the series (they are asymptotically equivalent because the first terms in the series are exponentially negligible): $$ a_k = \frac{1}{2} \int_1^{\infty} \frac{L \Delta^2}{ t^{\beta+\alpha}} \Big( 1 \, – \frac{\gamma L}{t^\alpha} \Big)^{2k} dt.$$ With the change of variable \(u = \frac{\gamma L}{t^\alpha}\), we get, after a short calculation, $$ a_k \sim \frac{L \Delta^2 }{2 \alpha (\gamma L)^{\frac{\beta-1}{\alpha}+1 }} \int_0^{\gamma L} u^{\frac{\beta-1}{\alpha}} (1-u)^{2k} du.$$ Laplace’s method then directly leads to $$ \tag{5} a_k \sim \frac{L \Delta^2 }{2 \alpha } \frac{\Gamma(\frac{\beta-1}{\alpha}+1)}{ (2 \gamma L k)^{\frac{\beta-1}{\alpha}+1 }}. $$

The rate above can be analyzed as follows:

• The rate is faster than \(1/k\) as soon as \(\| \theta_0\, – \theta_\ast\|_2^2\) is finite (\(\beta > 1\)), that is, the usual optimization rate is too pessimistic, not only in the constant, but in the power itself as well.
• When \(\| \theta_0\, – \theta_\ast\|_2^2\) is infinite (\(\beta \leqslant 1\)), then we get a rate slower than \(1/k\), which seems counter-intuitive given that equation \((3)\) is an upper bound. This is explained at the end of the post in the context of \(\lambda > 0\) (but you can already note that there is no contradiction here as the constant in front of \(1/k\) is infinite).

General \(\lambda> 0\). We first have to deal with the presence of two asymptotic regimes. This can be done by assuming that jointly \(k\) goes to infinity and \(\lambda\) goes to zero, with a fixed value of \(\lambda k\).

With the assumption in equation \((4)\), we have: $$a_k = \frac{1}{2}\sum_{i=1}^\infty \frac{\Delta^2}{i^{\beta}} \frac{1}{( 1+\frac{\lambda}{L} i^\alpha)^2} ( \lambda + L i^{-\alpha}) ( 1- \gamma ( \lambda + L i^{-\alpha}) )^{2k}.$$ We show at the end of the post that we have: $$ a_k \sim \frac{L \Delta^2 }{2 \alpha } \frac{\Gamma(\frac{\beta-1}{\alpha}+1)}{ (2\gamma L k)^{\frac{\beta-1}{\alpha}+1 }} \cdot c(\gamma \lambda k ),$$ with \(c(u) \approx 1\) if \(u \ll 1\), and \(c(u) \approx \frac{(\frac{\beta-1}{\alpha}+1)}{2u} e^{-2u}\) when \(u\gg 1\) (there is an explicit formula for \(c\) based on the exponential integral function).

This is the performance for \(\lambda =0\) in equation \((5)\), multiplied by an exponentially converging sequence. We can then see two behaviors that are often seen in optimization: first slow convergence in \((1/k)^{\frac{\beta-1}{\alpha}+1}\) like in the unregularized case, then exponential convergence at rate \(e^{-2 \lambda \gamma k}\), which starts to be visible when \(k \gg 1/(\gamma \lambda)\) (remember that \(\lambda\) is typically quite small). We exactly see these two regimes in the two experiments above, which exactly used our deterministic model.

Extension to random deviations to optimum. As mentioned earlier, we can consider the stochastic model $$\tag{6}\delta_i \sim \frac{\Delta}{i^{\beta/2}} \cdot \frac{1}{1+ \frac{\lambda}{L} i^\alpha} \cdot z_i,$$ with independent random variables \(z_i\) with \(\mathbb{E} [ z_i^2 ] = 1\) and \(\mathbb{E} [ z_i^4 ]\) finite. We show at the end of the post that the exact same equivalents are valid, but this time in probability (i.e., determistic convergence is replaced by convergence in probability). This is important for our machine learning context, as it may be easier to make assumptions on the regularity of the prediction function rather than on its specific coefficients on a particular eigenbasis.

Relationship to other upper bounds in optimization. Other quantities than \(\| \theta_0 \, – \theta_\ast\|_2^2\) have been considered, that use the Hessian matrix, such as \((\theta_0 \,- \theta_\ast)^\top H^{1-\rho} (\theta_0 \,- \theta_\ast)\) for \(\rho \geqslant 0\) (see [18], and [19, 20, 21] in the context of SGD, more on this next post), often referred to as a “source condition” (as described by [25] for statistical rates of convergence). Indeed, we have: $$ F(\theta_k)\, – F_\ast \leqslant \frac{1}{2 ( 2k \gamma )^\rho }(\theta_0\, – \theta_\ast)^\top H^{1-\rho} (\theta_0 \,- \theta_\ast) \sup_{u >0} u^{\rho}e^{-u},$$ which is equal to \(\displaystyle \frac{1}{2 ( 2k \gamma )^\rho }(\theta_0 \, – \theta_\ast)^\top H^{1-\rho} (\theta_0 \,- \theta_\ast) e^{-\rho} \rho^\rho.\) See also Table 3 from [22] for similar notions in convex optimization for \(\rho = -1, 0, 1\). Note however that these are still upper bounds and not asymptotic equivalents.

Before illustrating the asymptotic results above, we first provide a justification of the model in a machine learning context, using random features.

Random feature models

Within machine learning, gradient descent is typically used on the potentially regularized empirical risk (I will consider SGD in another post). To obtain a quadratic problem, we need a linear model and square loss, that is, $$F(\theta) = \frac{1}{2n} \sum_{i=1}^n \big( y_i \,- \theta^\top \varphi(x_i) \big)^2 + \frac{\lambda}{2} \| \theta \|_2^2 = \frac{1}{2n} \| y \,- \Phi \theta\|_2^2 + \frac{\lambda}{2} \| \theta \|_2^2 ,$$ with \(\Phi \in \mathbb{R}^{n \times d}\) the design matrix and \(y \in \mathbb{R}^n\) the response vector. Then the Hessian matrix \(H\) is equal to $$H = \frac{1}{n} \Phi^\top \Phi + \lambda I, $$ the regularized empirical second moment of the feature vector. Within most practical large-scale problems, the lowest eigenvalue of the data part \(\frac{1}{n} \Phi^\top \Phi \) is typically very small, so in this post, we will take \(\mu = \lambda\), that is, the source of strong convexity only comes from the regularizer (which is by design small, e.g., or order \(1/n\)). Moreover, we will consider dimensions \(d\) that diverge to infinity.

The function \(F\) has minimizer $$\tag{7} \theta_\ast = ( \Phi^\top \Phi + n \lambda I)^{-1} \Phi^\top y.$$ We initialize gradient descent at \(\theta_0=0\). In order to check if the model highlighted above makes sense, we need to select a model for the training data, and in particular the response vector \(y \in \mathbb{R}^n\) (we assume that the input data \(x_1,\dots,x_n \in \mathcal{X}\) are sampled i.i.d. from some distribution). We simply select \(y_i\) has a fixed function of \(x_i\), that is, \(y_i = f(x_i)\) for a well-chosen function \(f\) from \(\mathcal{X}\) to \(\mathbb{R}^d\). We then need to select a feature map \(\varphi: \mathcal{X} \to \mathbb{R}^d\), which we do now.

Random features. We consider a random feature model of the form \(\varphi(x)_i = \frac{1}{\sqrt{d}} \psi(x,v_i) \in \mathbb{R}\), where \(v_i\) is random (each of them sampled independently from the same distribution), for \(i=1,\dots,d\). When \(d\) tends to infinity, then the associated kernel function $$\sum_{i=1}^d \varphi(x)_i \varphi(x’)_i = \frac{1}{d} \sum_{i=1}^d \psi(x,v_i) \psi(x’,v_i)$$ converges to its expectation \(k(x,x’)\) (by the law of large numbers).

The kernel matrix \(\Phi \Phi^\top \in \mathbb{R}^{n \times n}\) is a classical quantity of interest in this context, and has the same non-zero eigenvalues as \(\Phi^\top \Phi\). As shown in last post, the sequence of eigenvalues of \(\Phi \Phi^\top\) is asymptotically equivalent to \(n\) times the eigenvalues of an infinite-dimensional covariance operator that depends only on the kernel \(k\) and the distribution of inputs. Moreover, for specific choices of kernels and input distributions, the decay of these eigenvalues is exactly as \(L / i^\alpha\), for the \(i\)-th eigenvalue, as reviewed in section 2.3 of [8], with the following classical examples that will be used in experiments below:

• Periodic translation-invariant kernels on \(\mathcal{X} = [0,1]\): Using Fourier features \(\psi(x,v) = e^{2i\pi v}\) for \(v \in \mathbb{Z}\) random (with the appropriate distribution), then we obtain kernels of the form \(k(x,x’) = \mathbb{E}[ e^{2i\pi v(x-x’)}]\). For the uniform distribution (of inputs) on \(\mathcal{X}=[0,1]\), and a distribution for \(v\) such that \(\mathbb{P}( v = i) \propto |i|^{-2s}\), we obtain eigenvalue decays as \(1/m^{2s}\) (with the Fourier basis as eigenvectors), i.e., \(\alpha = 2s\), for \(s\) positive integer. The space of associated models is the Sobolev space of functions with integrable \(s\)-th order derivative (see [9, 5] for details).
• Infinitely-wide one-hidden layer neural networks: For \(\mathcal{X} \subset \mathbb{R}^m\), we consider \(\psi(x,v) = \sigma(v^\top x)\), for \(v \in \mathbb{R}^m\) a random vector (with uniform distribution on the sphere), and \(\sigma\) an activation function. This corresponds to a one-hidden layer neural network with random input weights, and where only the output layer is optimized. On the unit \(\ell_2\)-sphere and using the \(s\)-th power of the rectified linear unit, we obtain \(\alpha = 1 + \frac{2s+1}{m-1}\), with an eigenbasis composed of spherical harmonics (see [10]).

Thus, with both a diverging number \(d\) of random features (so that we approach the limiting kernel function), and a diverging number \(n\) of observations (so that the eigenvalue decay of the covariance operator is reached), the model of decay for the unregularized part of the Hessian has the desired asymptotic behavior as \(L / i^\alpha\).

Label vector from Gaussian process. We assume that the function \(f\) such that \(y_i = f(x_i),\) \(i=1,\dots,n\), is sampled from a Gaussian process with covariance function / kernel \(q:\mathcal{X} \times \mathcal{X} \to \mathbb{R}\). Thus, if we denote \(Q \in \mathbb{R}^{n \times n}\) the corresponding kernel matrix, then \(y\) is Gaussian with covariance matrix \(Q\). The regularity of \(f\) depends on the regularity of the covariance function (see [17]).

There are thus two kernels and kernel matrices in our model: \(K\) for our inputs, and \(Q\) for our labels. Note that there is no “match” between model and labels if \(K = Q\); that is, if we sample a function from a Gaussian process with a certain covariance function it almost surely does not belong to the associated function space from this kernel function; this is well explained in [11] (and I personally find it surprising).

For our model to be asymptotically correct when \(n\) tends to infinity, we assume that the two kernel functions \(k\) and \(q\) have integral operators that lead to the same eigenfunctions, which implies that when \(n\) is large, the largest eigenvectors of \(K\) and \(Q\) are the same and that essentially, \(K\) and \(Q\) commute. This assumption is true for the two cases highlighted above and used in our experiments (Fourier basis for periodic kernels on \([0,1]\) and spherical harmonics for neural networks [10]).

If we denote the asymptotic eigenvalue equivalents as \(n L / i^\alpha\) for \(K\) and \(n M / i^\kappa\) for \(Q\), then, \(y\) is decomposed in this shared eigenbasis with components \(n^{1/2} M^{1/2} / i^{\kappa/2} \cdot z_i\), with \(z\) a standard Gaussian vector. This leads to, using equation \((7)\), $$\delta_i \sim \frac{\sqrt{n L / i^\alpha}}{n L / i^\alpha + n \lambda} n^{1/2} M^{1/2} / i^{\kappa/2} \cdot z_i \sim \frac{M^{1/2}/L^{1/2}}{i^{(\kappa-\alpha)/2}} \cdot \frac{1}{1+\frac{\lambda}{L} i^\alpha} z_i,$$ which is exactly our model in equation \((6)\), with \(\beta = \kappa \, – \alpha\) and \(\Delta = M^{1/2}/L^{1/2}\).

Note that this is only asymptotic when \(n\) goes to infinity, and obtained with rather informal arguments, but, as shown in experiments, it already gives good prediction of the actual performance for reasonable \(n\).

Adding noise. We could add noise to the labels, which corresponds to adding to \(\delta\) a component with \(\kappa=0\) and \(M= \frac{\sigma^2}{n}\). When \(n\) goes to infinity and \(\lambda\) is fixed, then the effect of the noise (unsurprisingly) goes away. We could also consider a dependence of \(\lambda\) in \(n\), but we ignore it here as we focus on optimization.

Experiments

We use the model above to test our asymptotic equivalents and compare them to actual performance. We first start with a situation, where all parameters \(\alpha, \beta, L, \Delta\) are known, before moving to a situation where there are not.

Translation-invariant kernels in \([0,1]\). In this context, we can exactly plant values of \(\alpha\) and \(\beta\), by taking kernel functions based on Bernoulli polynomials, where we have \(\alpha = 2s\) and \(\beta = 2t\), for integers \(s\), and \(t\) (see section 7.3.2 in [5]). Given that the kernel functions can be obtained in closed form, we can consider infinitely many random features by simply using \(\Phi\) as a square root of the kernel matrix. We use \(s=1\), and \(t = 1\) or \(t=2\), with the known values of \(L,M\). The two plots below show that even with \(n=512\) the model is quite accurate.

The first plot corresponds to an initial decay in \(1/k^{3/2}\), faster than the usual \(1/k\).

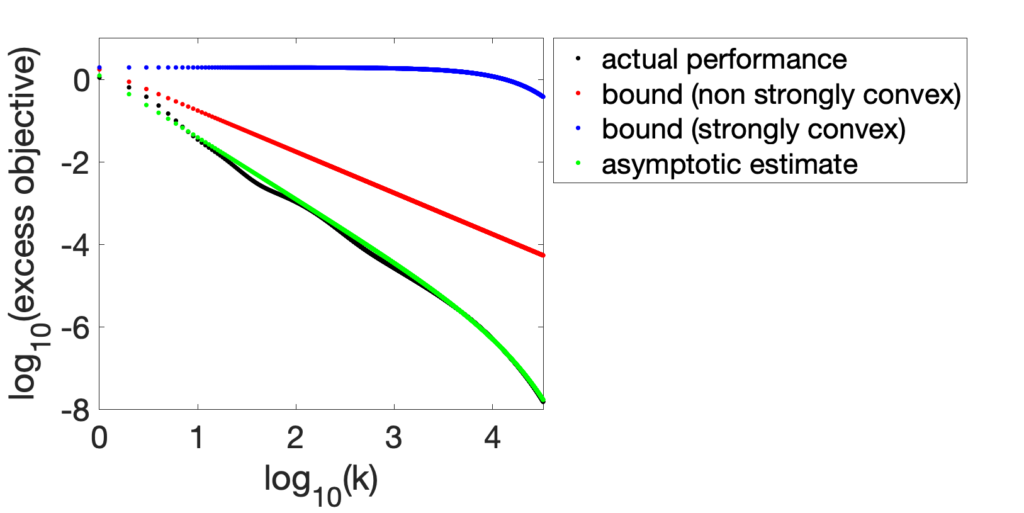
The second plot corresponds to an initial decay in \(1/k^{1/2}\), slower than the usual \(1/k\).

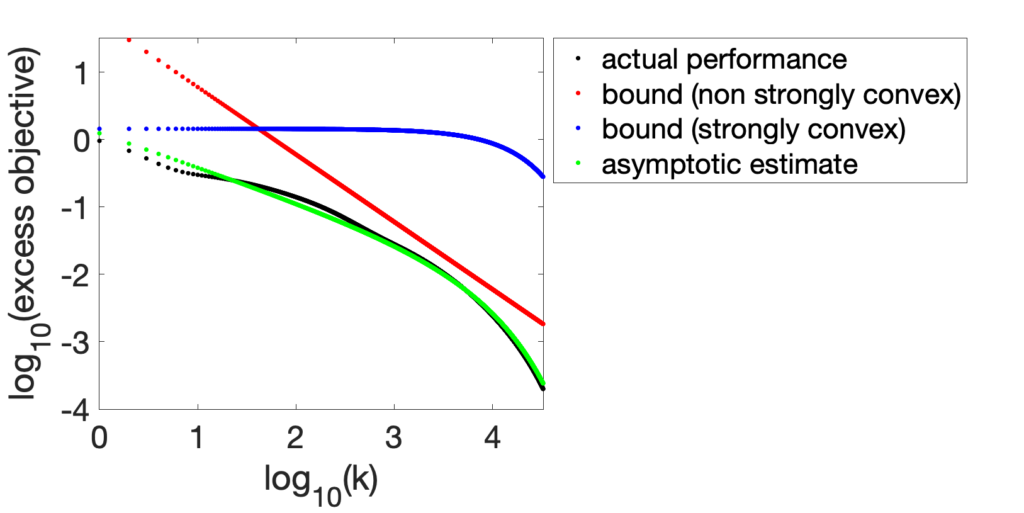
Neural networks with random features. We consider the same set up, but with now random features obtained by one-hidden layer neural network with sign activation function, with the two kernels \(k\) and \(q\) being equal. We use the same number \(d\) of random features as the number \(n\) of observations. We consider data on the unit sphere in \(\mathbb{R}^m\), for which we know that we have \(\alpha = 1 + \frac{1}{m-1}\), but no knowledge of the constant \(L\). To obtain it, we fit an affine function in log-log scale to the first \(n/4\) eigenvalues of the kernel matrices \(K\).

For reasonably large \(d\) (e.g., \(d=64\) below), the estimation of model parameters works well, and the asymptotic estimate is close to the actual performance, while for larger \(d\), the estimation is not as good, but while it qualitatively reflects the behavior. In particular, we can see a rate in \(1/k\) being too optimistic. Note also the weird behavior where the non-strongly convex bound starts way off and then almost touches the actual performance; this is explained at the end of the blog.

Acceleration

Because we have asymptotic bounds, we can compare performance of two different algorithms. We now consider a recursion that stores two iterates \(\theta_{k-1}\) and \(\theta_{k-2}\) and compute for \(k \geqslant 1\), \(\theta_k\) as $$\theta_k = \eta_{k-1} – \gamma F'(\eta_{k-1}) \ \mbox{ with } \ \eta_{k-1} = \theta_{k-1} + \Big(1 \, – \frac{2}{k} \Big) ( \theta_{k-1} – \theta_{k-2}).$$ This iteration is started at \(k=1\) with the convention \(\theta_{-1} = \theta_0\). This is a form of Nesterov acceleration [12], thoroughly studied in [13], where Lemma 3 shows that for \(k\geqslant 1\), $$F(\theta_k) \, – F_\ast = \frac{1}{2 \gamma} \sum_{i=1}^d \delta_i^2 \frac{ \sin^2 ( k \omega_i) }{ k^2 } ( 1- \gamma h_i)^{k+1}, $$ where the angle \(\omega_i \in [0,\pi/2]\) is defined through \(\sin \omega_i = \sqrt{ \gamma h_i }\).

As for gradient descent, with our assumptions we obtain, with \(\gamma = 1/L\), a similar integral equivalent: $$F(\theta_k) \, – F_\ast \sim \frac{L}{2} \int_1^{+\infty} \!\! \frac{\Delta^2}{t^\beta} \frac{ \sin^2 ( k \omega_t ) }{ k^2 } \Big( 1- \frac{1}{t^\alpha} \Big)^{k+1} dt $$ where the angle \(\omega_t \in [0,\pi/2]\) is defined through \(\sin \omega_t = \sqrt{ 1/ t^\alpha}\). We can then show that the oscillatory term will lead to a term \(1/2\) (by writing \(\sin^2 ( k \omega_t ) = \frac{1}{2}( 1 – \cos (2 k \omega_t ))\)), and get the equivalent $$F(\theta_k) \, – F_\ast \sim \frac{L \Delta^2}{4\alpha k^2 } \int_0^{1} u^{\frac{\beta- 1}{\alpha} – 1} e^{-u (k+1)} du, $$ which is then equivalent to, by Laplace’s method, $$F(\theta_k) \, – F_\ast \sim \alpha \frac{ L \Delta^2}{4 } \frac{\Gamma( \frac{\beta- 1}{\alpha})}{k^{\frac{\beta- 1}{\alpha}+2}}.$$ We thus obtain the same scaling law as for non-accelerated gradient descent but with an extra factor of \(1/k\), which is indeed always faster than gradient descent.

Note that the asymptotic equivalent requires that \(\frac{\beta- 1}{\alpha} > 0\), which excludes a comparison with gradient descent for \(\beta \leqslant 1\). A similar (more complicated) result holds as well in the strongly-convex case, and similar computations can be carried out for the heavy-ball method.

Going beyond

In this post, I provided a model of scaling laws specifically adapted to quadratic optimization problems minimized with (accelerated) gradient descent. An immediate worthwhile extension is stochastic gradient descent, which I will tackle in the next post, still using least-squares tools [14, 15], with similar scaling laws. Still in the convex domain, going beyond quadratics using tools from performance estimation problems (see [23] for a nice software package) remains an open problem. Even further (and even more an open problem), it would be great to obtain such theoretical scaling laws that match empirical performance for nonconvex optimization problems such as the minimization of all layers of deep neural networks.

Acknowledgements. I would like to thank Adrien Taylor, Raphaël Berthier, and Nicolas Flammarion for proofreading this blog post and making good clarifying suggestions.

References

[1] Larry Wasserman. All of Nonparametric Statistics. Springer Science & Business Media, 2006.
[2] Alexandre B. Tsybakov. Introduction to Nonparametric Estimation. Springer, 2009.
[3] Sebastian H. Seung, Haim Sompolinsky, and Naftali Tishby. Statistical mechanics of learning from examples. Physical Review A, 45(8):6056-6091, 1992.
[4] Marc Potters and Jean-Philippe Bouchaud. A First Course in Random Matrix Theory: for Physicists, Engineers and Data Scientists. Cambridge University Press, 2020.
[5] Francis Bach. Learning Theory from First Principles. MIT Press, 2024.
[6] Zhenyu Liao and Romain Couillet. The dynamics of learning: A random matrix approach. International Conference on Machine Learning, 2018.
[7] Richard B. Paris. The discrete analogue of Laplace’s method. Computers & Mathematics with Applications. 61(10):3024:3034, 2011.
[8] Francis Bach. On the equivalence between kernel quadrature rules and random feature expansions. Journal of Machine Learning Research, 18(21):1-38, 2017.
[9] Grace Wahba. Spline Models for Observational Data. Society for Industrial and Applied Mathematics, 1990.
[10] Francis Bach. Breaking the Curse of Dimensionality with Convex Neural Networks. Journal of Machine Learning Research, 18(19):1-53, 2017.
[11] Motonobu Kanagawa, Philipp Hennig, Dino Sejdinovic, and Bharath K. Sriperumbudur. Gaussian processes and kernel methods: A review on connections and equivalences. arXiv preprint arXiv:1807.02582, 2018.
[12] Yurii Nesterov. A method of solving a convex programming problem with convergence rate \(O(1/k^2)\). Soviet Mathematics Doklady, 27(2):372–376, 1983.
[13] Nicolas Flammarion and Francis Bach. From Averaging to Acceleration, There is Only a Step-size. International Conference on Learning Theory (COLT), 2015.
[14] Arie Feuer and Ehud Weinstein. Convergence analysis of LMS filters with uncorrelated Gaussian data. IEEE Transactions on Acoustics, Speech, and Signal Processing, 33(1):222-230, 1985.
[15] Alexandre Défossez and Francis Bach. Averaged least-mean-square: bias-variance trade-offs and optimal sampling distributions. International Conference on Artificial Intelligence and Statistics (AISTATS), 2015. 
[16] Alnur Ali, J. Zico Kolter, and Ryan J. Tibshirani. A continuous-time view of early stopping for least squares regression. International Conference on Artificial Intelligence and Statistics, 2019. 
[17] Christopher K. I. Williams and Carl Edward Rasmussen. Gaussian Processes for Machine Learning. MIT Press, 2006.
[18] Arkadi S. Nemirovsky. Information-based complexity of linear operator equations. Journal of Complexity, 8(2), 153-175, 1992.
[19] Aymeric Dieuleveut, Nicolas Flammarion, and Francis Bach. Harder, Better, Faster, Stronger Convergence Rates for Least-Squares Regression. Journal of Machine Learning Research, 18(101):1-51, 2017.
[20] Loucas Pillaud-Vivien, Alessandro Rudi, and Francis Bach. Statistical optimality of stochastic gradient descent on hard learning problems through multiple passes. In Advances in Neural Information Processing (NeurIPS), 2018.
[21] Raphaël Berthier, Francis Bach, and Pierre Gaillard. Tight Nonparametric Convergence Rates for Stochastic Gradient Descent under the Noiseless Linear Model. Advances in Neural Information Processing Systems (NeurIPS), 2020.
[22] Adrien B. Taylor, Julien M. Hendrickx, and François Glineur. Exact worst-case convergence rates of the proximal gradient method for composite convex minimization. Journal of Optimization Theory and Applications, 178: 455-476, 2018.
[23] Baptiste Goujaud, Céline Moucer, François Glineur, Julien M. Hendrickx, Adrien B. Taylor, Aymeric Dieuleveut. PEPit: computer-assisted worst-case analyses of first-order optimization methods in Python, Mathematical Programming Computation, 2024.
[24] Marcus Hutter. Learning curve theory. arXiv preprint arXiv:2102.04074, 2021.
[25] Andrea Caponnetto and Ernesto De Vito. Optimal rates for the regularized least-squares algorithm. Foundations of Computational Mathematics, 7(3):331–368, 2007.
[26] Jared Kaplan, Sam McCandlish, et al. Scaling laws for neural language models. arXiv preprint arXiv:2001.08361, 2020.
[27] Jordan Hoffmann, Sebastian Borgeaud, Arthur Mensch, et al. Training Compute-Optimal Large Language Models. Advances in Neural Information Processing (NeurIPS), 2022.
[28] Terence Tao. Topics in random matrix theory. American Mathematical Society, 2012.

Asymptotic expansion – strongly convex case

We aim to find an asymptotic equivalent to $$a_k = \frac{1}{2} \sum_{i=1}^\infty \frac{\Delta^2}{i^{\kappa – \alpha}} \frac{1}{( 1+\frac{\lambda}{L} i^\alpha)^2} ( \lambda + L i^{-\alpha}) ( 1- \gamma ( \lambda + L i^{-\alpha}) )^{2k}.$$ We can factorize the exponential term, thus leading to $$a_k = \frac{L \Delta^2 }{2} ( 1- \gamma \lambda)^{2k} \sum_{i=1}^\infty \frac{1}{i^{\kappa}} \frac{1}{ 1+\frac{\lambda}{L} i^\alpha} \Big( 1- \frac{\gamma L}{1-\gamma \lambda} \frac{1}{i^{\alpha}} \Big)^{2k}.$$ In order to use an asymptotic analysis with a single parameter (here \(k\)), we take \(\lambda = L \frac{\nu}{k}\), and, with the usual integral equivalent, we get $$a_k \sim \frac{L \Delta^2 }{2} ( 1 – \gamma L \frac{\nu}{k})^{2k} \int_1^\infty \frac{1}{t^{\kappa }} \frac{1}{ 1+\frac{\nu}{k}t^\alpha} \Big( 1- \frac{\gamma L }{t^{\alpha}} \Big)^{2k}dt.$$ With the change of variable \(u = 2k \gamma L /t^\alpha\), we get (also using the exponential equivalent, which is the core technique being Laplace’s method), $$a_k \sim \frac{L \Delta^2 }{2\alpha} e^{-2\nu \gamma L } \frac{1}{(2k\gamma L)^{\frac{\beta-1}{\alpha}+1}} \int_0^1 \frac{u}{u+{2 \gamma L \nu} } u^{\frac{\beta-1}{\alpha}} e^{-u} du.$$ We can now use the exponential integral function \(E_\omega\), which satisfies $$\int_0^{+\infty} \frac{e^{-u} u^{\omega-1}}{u+z} du = e^z E_\omega(z) \Gamma(\omega),$$ to get (using \( \nu \gamma L = \gamma \lambda k\)): $$a_k \sim \frac{L \Delta^2 }{2\alpha} \frac{\Gamma( \frac{\beta-1}{\alpha}+1)}{(2k\gamma L)^{\frac{\beta-1}{\alpha}+1}} \cdot \Big( \frac{\beta-1}{\alpha}+1\Big)E_{\frac{\beta-1}{\alpha}+2}(2\nu \gamma L),$$ which is equal to the non-strongly convex result obtained earlier times \(c( \nu \gamma L) = \big(\frac{\beta-1}{\alpha}+1\big)E_{\frac{\beta-1}{\alpha}+2}(2\nu \gamma L)\).

When \(z\) tends to zero, then \(c(z)\) tends to one (leading to the non-strongly convex result), while if \(z\) is tending to infinity, then it is equivalent to \(\big(\frac{\beta-1}{\alpha}+1\big) \frac{e^{-2z}}{2z}\), leading to exponential convergence. The overall behavior is essentially the same as \(e^{-2z}\).

Random minimizer

For \(\lambda=0\), we can consider a model \(\delta_i = \frac{\Delta}{i^{\beta/2}} z_i\), where \(z_i\) is such that \(\mathbb{E}[z_i^2]=1\) and \(\mathbb{E}[z_i^4] \) is finite. If we denote \(a_k\) the random performance, we have shown that \(\mathbb{E}[a_k] \sim \frac{\mbox{cst} }{k^{ \frac{\beta-1}{\alpha}+1}}\), while we can also show with the exact same techniques (Laplace’s method) that $$ \mathbb{E}[a_k^2] \sim \frac{\mbox{cst} }{k^{ 2 \frac{\beta-1}{\alpha}+2 + \frac{1}{\alpha}}} \propto \mbox{cst} \big(\mathbb{E}[a_k] \big)^2 \cdot \frac{1}{k^{1/\alpha}}.$$ By Chebyshev’s inequality, this implies that our equivalents are true in probability.

“Weird” behavior explained

In the last plot (neural network simulation), we see a weird phenomenon where the non-strongly convex upper bound becomes almost tight at a certain point, when the early rate \(1/k^\omega\) is such that \(\omega = \frac{\beta-1}{\alpha}+1 \in (0,1)\).

Here is an explanation: the traditional bound is proportional to \(\| \delta\|_2^2\), which has the following equivalent (still using Laplace’s method), when \(\lambda = L \nu / k\): $$\| \delta\|_2^2 \sim \Delta^2 \sum_{i=1}^{+\infty} \frac{1}{i^\beta} \frac{1}{(1 + \nu i^\alpha / k)^2} \sim \Delta^2 \int_{1}^{+\infty} \frac{1}{t^\beta} \frac{dt}{(1 + \nu t^\alpha / k)^2}. $$ By the change of variable \(u = \nu t^\alpha / k\), we get $$\| \delta\|_2^2 \sim \Delta^2\int_0^{+\infty} \frac{k}{\nu \alpha} \big( \frac{\nu}{ku} \big)^\omega \frac{du}{(1+u)^2} = \Delta^2\frac{\nu^{\omega-1}}{k ^{\omega-1} \alpha} \frac{\pi \omega}{\sin (\pi \omega) }.$$ Thus, the non-strongly convex bound from equation \((3)\) has equivalent $$ \frac{L \Delta^2 }{4e }\frac{\nu^{\omega-1}}{k ^{\omega} \alpha} \frac{\pi \omega}{\sin (\pi \omega) },$$ while our asymptotic result is $$ \frac{L \Delta^2 }{2\alpha} \frac{\Gamma( \omega +1)}{(2k)^{\omega}} \cdot E_{\omega+1}(2\nu).$$ When \(\omega\) tends to zero, then the ratio between the two bounds tends to $$\frac{1}{2e \nu E_1(2\nu)} \geqslant \frac{1}{e \max_{u >0 } u E_1(u) } \approx 1.3069 > 1.$$ The curves do not touch but end up indeed very close for a certain value of \(\nu\) (which correspond to \(k\) being a constant times \(1/\lambda\), which we observe).