Last month, we saw that self-concordance is a key property in optimization, to use local quadratic approximations in the sharpest possible way. In particular it was an affine-invariant quantity leading to a simple and elegant analysis of Newton method. The key assumption was a link between third and second-order derivatives, which took the following form for one-dimensional functions, $$|f^{\prime\prime\prime}(x)| \leqslant 2 f^{\prime\prime}(x)^{3/2}.$$ Alas, some of the most classical smooth functions appearing in machine learning are not self-concordant with this particular link between derivatives. The main example is the logistic loss, which is widely used across machine learning.
Indeed, if we take this logistic loss function \(f(x) = \log ( 1 + \exp(-x))\), it satisfies $$ f^\prime(x) = \frac{ -\exp(-x)}{1+\exp(-x)} =\ – \frac{1}{1+\exp(x)} = \ – \sigma(-x),$$ where \(\sigma\) is the usual sigmoid function defined as \(\sigma(x) = \frac{1}{1+\exp(-x)}\), and which is increasing from \(0\) to \(1\). We then have \(f^{\prime\prime}(x) = \sigma(x) ( 1- \sigma(x) )\) and \(f^{\prime \prime \prime}(x) = \sigma(x) ( 1- \sigma(x) )( 1 – 2 \sigma(x) )\) leading to $$|f^{\prime\prime\prime}(x)| \leqslant f^{\prime\prime}(x).$$ See below for plots of the logistic loss (left) and its derivatives (right).
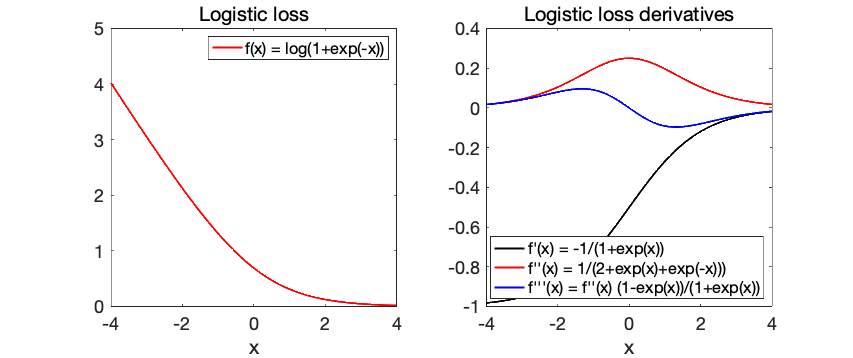
There is thus a link between third and second-order derivatives, but without the power \(3/2\). Does this difference really matter? In this post, I will show how some properties from classical self-concordance can be extended to this slightly different notion. We will then present applications to stochastic gradient descent as well as the statistical analysis of generalized linear models, and in particular logistic regression.
I will describe applications to Newton method for large-scale logistic regression [8] in later posts (you read well: Newton method for large-scale machine learning can be useful, in particular for severely ill-conditioned problems).
\(\nu\)-self-concordance
A function \(f: C \subset \mathbb{R} \to \mathbb{R}\) is said \(\nu\)-self-concordant on the open interval \(C\) if and only if it is convex, three-times differentiable on \(C\), and there exists \(R > 0\), such that $$\tag{1}\forall x \in C, \ |f^{\prime\prime\prime}(x)| \leqslant R f^{\prime\prime}(x)^{\nu\: \! /2}.$$
Note the difference with classical self-concordance (which corresponds to \(\nu=3\) and \(R=2\)). All positive powers are possible (see [1]), but we will focus primarily on \(\nu=2\), for which most of the properties below were derived in [2].
Note that the definition above in one dimension is still “affine-invariant” if the constant \(R\) is allowed to change (that is, if it is true for \(f\), it is true for \(x \mapsto f(ax)\) for any \(a\)). However, unless \(\nu = 3\), this will not be true in higher dimension, and therefore, the analysis of Newton method will be more complicated.
For a convex function defined on a convex subset \(C\) of \(\mathbb{R}\), we need the same property along all rays, or equivalently, if \(f^{\prime\prime\prime}(x)[h,h^\prime,h^{\prime\prime}]= \sum_{i,j,k=1}^d h_i h_j^\prime h^{\prime\prime}_k \frac{\partial^3 f}{\partial x_i \partial x_j \partial x_k}(x)\) is the third-order tensor (with three different arguments, as needed below) and \(f^{\prime\prime}(x)[h,h] = \sum_{i,j=1}^d h_i h_j \frac{\partial^2 f}{\partial x_i \partial x_j}(x)\) the symmetric second-order one, then there exists \(R\) such that $$\tag{2} \forall x \in C, \ \forall h \in \mathbb{R}^d , \ |f^{\prime\prime\prime}(x)[h,h^\prime,h^{\prime}]| \leqslant R \| h\| \cdot f^{\prime\prime}(x)[h^\prime,h^{\prime}],$$ where \(\| h\|\) is the standard Euclidean norm of \(h\). Note here the difference with classical self-concordance where we could consider the symmetric third-order tensor (that is, no need for \(h^\prime\) and \(h^{\prime\prime}\)), and only the Euclidean norm based on the Hessian \(f^{\prime\prime}(x)\) was used.
Examples. One can check that if \(f\) and \(g\) are \(2\)-self-concordant, then so is their average \(\frac{1}{2} ( f+g ) \) with the same constant \(R\) (this is one key advantage over \(3\)-self-concordance). Moreover, if \(f\) is \(2\)-self-concordant with constant \(R\), then \(g(x) = f(Ax)\) is also \(2\)-self concordant, with constant \(R \| A\|_{\rm op}\).
Classical examples are all linear and quadratic functions (with constant \(R = 0\)), the exponential function and the logistic loss \(f(x) = \log(1+\exp(-x))\), both with constant \(R=1\). This extends to the “log-sum-exp” function \(f(x) = \log\big( \sum_{i=1}^d \exp(x_i)\big)\), which is \(2\)-self-concordant with constant \(R = \sqrt{2}\). More generally, as shown at the end of the post, any log-partition function of the form $$ f(x) = \log \Big( \int_\mathcal{A} \exp( \varphi(a)^\top x) d\mu(a) \Big) $$ arising from generalized linear models with bounded features, will be \(2\)-self-concordant, with constant the diameter of the set of features. Thus, self-concordance applies to all generalized linear models with the canonical link function. This includes softmax regression (for multiple classses), conditional random fields, and of course logistic regression which I will focus on below.
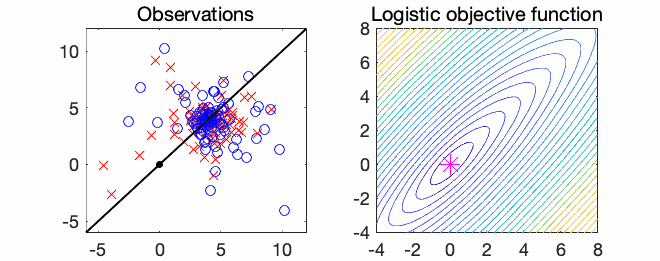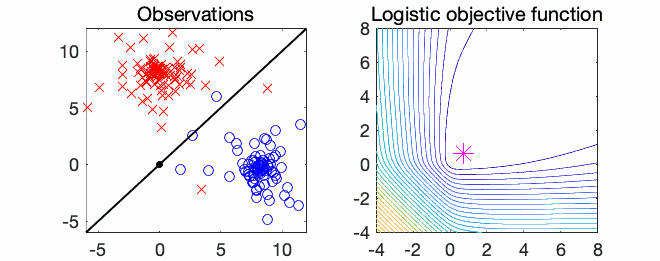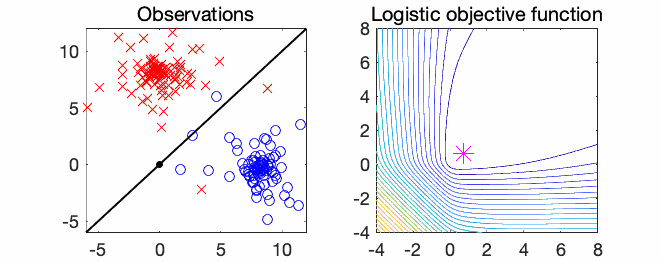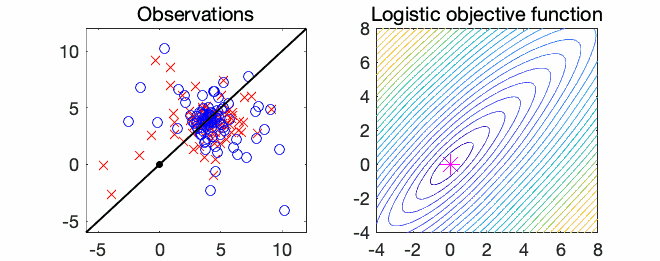
Logistic regression. The most classical example is thus logistic regression, with $$f(x) = \frac{1}{n} \sum_{i=1}^n \log(1 + \exp( – x^\top a_i b_i ) ),$$ for observations \((a_i,b_i) \in \mathbb{R}^d \times \{-1,1\}\). See an example below in \(d=2\) dimensions.
Properties in one dimension. Mimicking what was done last month, a nice reformulation of Eq. (1) (which is one-dimensional) is $$ \big| \frac{d}{dx} \big( \! \log( f^{\prime\prime}(x)) \big) \big| = \big| f^{\prime\prime\prime}(x) f^{\prime \prime}(x)^{-1} \big| \leqslant R,$$ which allows to define upper and lower bounds on \(f^{\prime \prime}(x)\) by integration, as, for \(x > 0\), $$ – Rx \leqslant \log( f^{\prime\prime}(x)) \, – \log(f^{\prime\prime}(0)) \leqslant Rx,$$ which can be transformed into (by isolating \(f^{\prime\prime}(x)\)): $$ \tag{3} f^{\prime\prime}(0) \exp(\ – R x ) \leqslant f^{\prime\prime}(x) \leqslant f^{\prime\prime}(0) \exp( R x ).$$ We thus obtain global upper and lower bounds on \(f^{\prime\prime}(x)\).
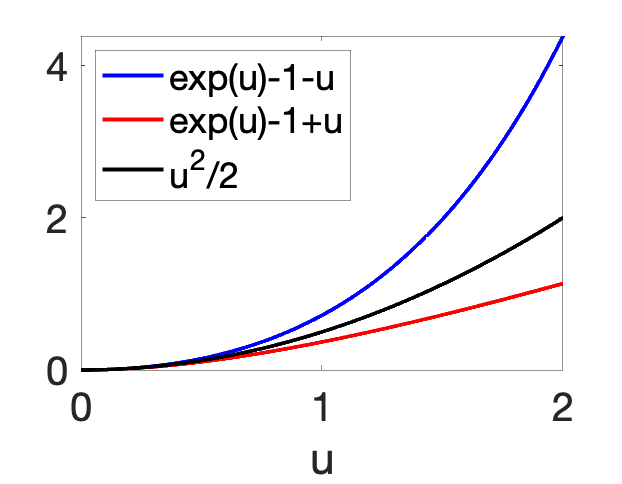
We can then integrate Eq. (3) twice between \(0\) and \(x\) to obtain lower and upper bounds on \(f^\prime\) and then \(f\): $$ f^{\prime\prime}(0) \frac{1-\exp( \ – R x )}{R} \leqslant f^\prime(x)-f^\prime(0) \leqslant f^{\prime\prime}(0) \frac{\exp( R x )\ – 1}{R},$$ and $$ \tag{4} \!\!\!\!\!\! f^{\prime\prime}(0) \frac{\exp( \ – R x ) + Rx \ – 1}{R^2}\leqslant f(x) \ – f(0) \ – f^\prime(0) x \leqslant f^{\prime\prime}(0) \frac{\exp( R x ) \ – Rx \ – 1}{R^2}.$$ We thus get a bound $$f(x) \ – f(0) \ – f^\prime(0) x \in f^{\prime\prime}(0) \frac{x^2}{2} \cdot [ \rho(-Rx), \rho(Rx) ],$$ with \(\displaystyle \rho(u) =\ \frac{\exp( u ) \ – u\ – 1}{u^2 / 2 } \sim 1 \) when \(u\to 0\), that is, the second-order expansion is tight at \(x =0\), but leads to global lower and upper bounds. These upper and lower Taylor expansions are illustrated below.
Properties in multiple dimensions. The properties above in Eq. (3) and (4) directly extend to multiple dimensions. For any \(x \in C\), then for any \(\Delta \in \mathbb{R}^d\), we have upper and lower bounds for the Hessian, the gradient (not presented below) and the functions value at \(x + \Delta\), that is, denoting by \(\| \cdot \|\) the standard Euclidean norm $$\tag{5}\exp(\ – R\|\Delta\|) f^{\prime \prime}(x) \preccurlyeq f^{\prime \prime}(x+\Delta) \preccurlyeq \exp( R\|\Delta\|) f^{\prime \prime}(x),$$ and $$\tag{6} \!\!\!\!\!\!\!\!\! \frac{ \Delta^\top f^{\prime \prime}(x) \Delta}{2} \rho(-R \|\Delta\|_2) \leqslant f(x+\Delta)\ -f(x) \ – f^\prime(x)^\top \Delta \leqslant \frac{ \Delta^\top f^{\prime \prime}(x) \Delta}{2} \rho(R \|\Delta\|_2).\! $$ These approximations are “second-order tight” at \(\Delta=0\), that is, the term in \(f^{\prime\prime}(x)\) in Taylor expansion around \(x\) is exact. These can be derived by considering \(g(t) = f(x+ t\Delta)\), which is \(2\)-self-concordant with constant \(R \|\Delta\|_2\), and applying the one-dimensional properties above in Eqs. (2) and (3) between \(0\) and \(1\).
Avoiding exponentially decaying constants. In this post, I will focus primarily on the use self-concordant functions in optimization (stochastic gradient descent in this post and Newton method in another post) as well as in statistics.
The main benefit of using self-concordance is to avoid exponential constants traditionally associated with the analysis of logistic regression. Indeed, for the logistic loss, the second-derivative at \(x\) is is equal to \(\sigma(x) ( 1 – \sigma(x) )\) and is equivalent to \(\exp(-|x|)\) when \(| x| \) is large. Thus, if we are willing to only apply the logistic loss to small values of \(|x|\), let’s say less than \(M\), then the logistic loss is strongly-convex with constant greater than \(\exp(-M)\). Therefore, we can apply many results in optimization and statistics that apply to such losses. However, all of these results will be impacted by the constant \(\exp(-M)\), which is strictly positive but can be very small. With self-concordance, the analysis will get rid of these annoying constants and replace them by eigenvalues of Hessian matrices at the optimum, which are typically much larger (note that in the worst case, the exponential constants are unavoidable [3]).
Adaptivity of stochastic gradient descent
I have not written about stochastic gradient descent for quite a while. Self-concordance gives me the occasion to talk about adaptivity.
It is well known that for smooth convex functions, gradient descent will converge exponentially fast if the function is also strongly-convex (essentially all eigenvalues of all Hessians being strictly positive). If the problem is ill-conditioned, then the exponential convergence rate turns into a rate of \(O(1/t)\) where \(t\) is the number of iterations. Gradient descent is adaptive as the exact same algorithm (with constant step-size or line-search) can be applied without the need to know the strong-convexity parameter. Moreover, if locally around the global optimum, the Hessians are better conditioned, gradient descent will also benefit from it. Therefore, gradient descent is great! What about stochastic gradient descent (SGD)?
It turns out that similar adaptivity exists for a well-defined version of SGD, and that self-concordance is one way to achieve simple non-asymptotic bounds (asymptotic bounds exist more generally [4]).
Logistic regression. We consider the logistic regression problem where we aim to minimize the expectation $$f(x) = \mathbb{E}_{a,b} \log( 1 + \exp(-b a^\top x) ) = \mathbb{E}_{a,b} g(x|a,b) ,$$ where \((a,b) \in \mathbb{R}^d \times \{-1,1\}\) is a pair of input \(a\) and output \(b\) (hopefully, the machine learning police will excuse my use of \(x\) as the parameter and not the input). We are given \(n\) independent and identically distributed observations \((a_1,b_1),\dots, (a_n,b_n)\) and we aim at finding the minimizer \(x_\ast\) of \(f\) (which is the logistic loss on unseen data), which we assume to exist. We assume that the feature norms \(\|a\|\) are almost surely bounded by \(R\).
Note here that we are not trying to minimize the empirical risk and by using a single pass, we obtain bounds on the generalization performance. This is one of the classical benefits of SGD.
Averaged stochastic gradient descent. We consider the stochastic gradient recursion: $$x_i = x_{i-1} – \gamma_i g^\prime(x_{i-1}|a_i,b_i),$$ for \(i=1,\dots,n\), with a single pass over the data. We also consider the average iterate \(\bar{x}_n = \frac{1}{n+1} \sum_{i=0}^{n} x_i\).
Standard results from the stochastic gradient descent literature [5, 6] show that if \(\gamma_i = \frac{1}{R^2 \sqrt{i}}\), then, up to universal (small) constants, $$ \mathbb{E} f(\bar{x}_i)\ – f(x_\ast) \leqslant (1 + R^2 \| x_0 – x_\ast\|^2) \frac{\log n}{\sqrt{n}}.$$ If in addition, the function \(f\) is \(\mu\)-strongly-convex, then with the step-size \(\gamma_i = \frac{1}{\mu i}\), up to universal (small) constants, $$ \mathbb{E} f(\bar{x}_i) \ – f(x_\ast) \leqslant \frac{R^2 \log n}{n\mu}.$$ The strongly convex result seems beneficial as we get a rate in \(O(( \log n) / n)\) instead of \(O(( \log n) / \sqrt{n})\), but, (1) it depends on \(\mu\), which can be very small in problems in high dimension \(d\), (2) it depends on this global strong-convexity constant \(\mu\), that is a lower bound on all Hessians, which is zero for logistic regression unless a projection step is used (and with exponentially small constant as explained above), and (3) the step-size has to be adapted.
Adaptivity. Wouldn’t it be great if these three problems could be solved at once? This is what I worked on a few years ago [7], where I showed that for constant step-size \(\gamma\) proportional to \(\frac{1}{R^2 \sqrt{n}}\) (thus dependent on the total number of gradient steps), we have. up to constants: $$ \mathbb{E} f(\bar{x}_i)\ – f(x_\ast) \leqslant (1 + R^2 \| x_0 – x_\ast\|^2) \frac{1}{\sqrt{n}},$$ and $$ \mathbb{E} f(\bar{x}_i)\ – f(x_\ast) \leqslant (1 + R^4 \| x_0 – x_\ast\|^4) \frac{R^2 }{\mu_\ast n},$$ where \(\mu_\ast\) is the smallest eigenvalue of the Hessian \(f^{\prime\prime}(x_\ast)\) at the optimum. The two bounds are always satisfied and one can be bigger than the other depending on \(n\) and the condition number \(R^2 / \mu_\ast\).
We thus get (almost) the best of all worlds! The proof relies strongly on self-concordance and applies to all generalized linear models. Note that (a) no new algorithm is proposed here, I am simply providing partial theoretical justifications why a classical algorithm works so well, (b) this is only an upper-bound on performance (more on this below).
Generalization bounds for generalized linear models
Beyond optimization, the use of self-concordant can make the non-asymptotic statistical analysis of logistic regression, and more generally all generalized linear models, sharper in the regularized unregularized setting [2, 10], with \(\ell_1\)-norm [10], or with non-parametric kernel-based models [2, 9]. The first benefit is to avoid exponential constants associated with usual strong-convexity arguments of the loss (which can also be achieved with other tools, see [11]). But there is another important benefit that requires some digression.
Asymptotic statistics is great… Supervised learning through empirical risk minimization is the workhorse of machine learning. It can be analyzed from different perspectives and with different tools. As shown in the great book by Aad Van der Vaart [12], asymptotics statistics is a very clean way of understanding the behavior of statistical estimators when the number of observations \(n\) goes to infinity.
Empirical risk minimization is indeed an example of M-estimation problems (estimators based on minimizing the empirical average of some loss functions), and it is known that under general conditions, the estimator has a known asymptotic mean and variance (with the traditional Fisher information matrices), which leads to an asymptotic equivalent of the unseen population risk (e.g., the “test error”). We recover the usual \(d/n\) bound for unregularized problems as well as dimension-independent results when using regularization with squared Euclidean norms (then with worse dependence in \(n\)).
Because we deal with limits, one can formally compare two methods by favoring the one with the smallest asymptotic risk. This is not possible when non-asymptotic upper bounds are available: the fact that they are true for all \(n\) is a strong benefit, but since they are only bounds, they don’t say anything about which method is best.
… But it is only asymptotic. Of course, these comparisons are only true in the limit of large \(n\), and, in particular for high-dimensional problems (e.g., data and/or parameters in large dimensions), we are unlikely to be in the asymptotic regime. So we cannot really rely only on letting \(n\) go to infinity. Moreover, these asymptotic limits typically depend on some information which is not available at training time. But does this mean that we have to throw away all asymptotic results?
Self-concordance to the rescue. Since many of the asymptotic results are obtained by second-order Taylor expansions, we need non-asymptotic ways of dealing with these expansions, which is exactly what self-concordance allows you to do (with some extra effort of course). Therefore the best of both worlds can be achieved with such tools; see, e.g., [9, 10], for examples of analysis, and [13, 14] for other tools that can achieve similar results. It is then possible to prove that some asymptotic expansions are valid non-asymptotically.
Conclusion
In this post I focused on two aspects of self-concordant analysis for logistic regression and its extensions, namely adaptivity of stochastic gradient descent and statistical generalization bounds.
In a later post, I will go back to Newton’s method, where the lack of affine invariance of \(2\)-self-concordance makes the analysis more complicated. However it will come with some interesting benefits for large-scale severely ill-conditioned problems [8]. You may wonder why we should bother with Newton method for large-scale machine learning when stochastic gradient descent, with or without variance reduction, seems largely enough. Stay tuned!
References
[1] Tianxiao Sun, and Quoc Tran-Dinh. Generalized self-concordant functions: a recipe for Newton-type methods. Mathematical Programming 178(1): 145-213, 2019.
[2] Francis Bach. Self-Concordant Analysis for Logistic Regression. Electronic Journal of Statistics, 4, 384-414, 2010.
[3] Elad Hazan, Tomer Koren, and Kfir Y. Levy. Logistic regression: Tight bounds for stochastic and online optimization. Proceedings of the International Conference on Learning Theory (COLT), 2014.
[4] Boris T. Polyak, and Anatoli B. Juditsky. Acceleration of stochastic approximation by averaging. SIAM journal on control and optimization, 30(4):838-855, 1992.
[5] Arkadi Nemirovski, Anatoli Juditsky, Guanghui Lan, and Alexander Shapiro. Robust stochastic approximation approach to stochastic programming. SIAM Journal on optimization, 19(4), 1574-1609, 2009.
[6] Francis Bach, and Eric Moulines. Non-asymptotic analysis of stochastic approximation algorithms for machine learning. Advances in Neural Information Processing Systems (NIPS), 2011.
[7] Francis Bach. Adaptivity of averaged stochastic gradient descent to local strong convexity for logistic regression. Journal of Machine Learning Research, 15(Feb):595−627, 2014.
[8] Ulysse Marteau-Ferey, Francis Bach, Alessandro Rudi. Globally convergent Newton methods for ill-conditioned generalized self-concordant Losses. Advances in Neural Information Processing Systems (NeurIPS), 2019.
[9] Ulysse Marteau-Ferey, Dmitrii Ostrovskii, Francis Bach, Alessandro Rudi. Beyond Least-Squares: Fast Rates for Regularized Empirical Risk Minimization through Self-Concordance. Proceedings of the International Conference on Learning Theory (COLT), 2019
[10] Dmitrii Ostrovskii, Francis Bach. Finite-sample Analysis of M-estimators using Self-concordance. Electronic Journal of Statistics, 15(1):326-391, 2021.
[11] Sham Kakade, Ohad Shamir, Karthik Sridharan, and Ambuj Tewari. Learning exponential families in high-dimensions: Strong convexity and sparsity. In Proceedings of the international conference on artificial intelligence and statistics (AISTATS), 2010.
[12] Aad W. Van der Vaart. Asymptotic Statistics. Cambridge University Press, 2000.
[13] Vladimir Spokoiny. Parametric estimation. Finite sample theory. The Annals of Statistics, 40(6), 2877-2909, 2012.
[14] Tomer Koren, and Kfir Y. Levy. Fast Rates for Exp-concave Empirical Risk Minimization. Advances in Neural Information Processing Systems (NIPS), 2015.
Self-concordance for generalized linear models
We consider a probability distribution on some set \(\mathcal{A}\), with density $$\exp\big( \varphi(a)^\top x) \ – f(x) \big)$$ with respect to the positive measure \(d\mu\), with \(f(x)\) the log-partition function, defined so that the total mass is one, that is, $$ f(x) = \log \Big( \int_\mathcal{A} \exp( \varphi(a)^\top x) d\mu(a) \Big). $$ We assume the feature vector \(\varphi(a)\) and the parameter \(x\) are in \(\mathbb{R}^d\).
The theory of exponential families tells us that the function \(f(x)\) is the “cumulant generating” function. That is, the cumulants of \(\varphi(a)\) for the probability distribution defined by \(x\), are exactly the derivatives of \(f\) taken at \(x\). More precisely, for the usual mean and covariance matrix, we get $$ \mathbb{E}_{a|x} \varphi(a) = f^\prime (x),$$ $$ \mathbb{E}_{a|x} \big(\varphi(a) \ – f^\prime (x)\big) \otimes \big(\varphi(a) \ – f^\prime (x)\big) = f^{\prime\prime}(x).$$ For the third order cumulant, we get: $$ \mathbb{E}_{a|x} \big(\varphi(a)\ – f^\prime (x)\big)\otimes \big(\varphi(a)\ – f^\prime (x)\big) \otimes \big(\varphi(a) \ – f^\prime (x)\big) = f^{\prime\prime\prime}(x).$$ Thus, for any \(h \in \mathbb{R}^d\), \(\big(\varphi(a) \ – f^\prime (x)\big)^\top h \leqslant \| h\| D\), where \(D\) is the diameter of the set \(\{ \varphi(a), \ a \in \mathcal{A} \}\), which leads to the desired \(2\)-self-concordance property.