Sums-of-squares for dummies: a view from the Fourier domain

In these last two years, I have been studying intensively sum-of-squares relaxations for optimization, learning a lot from many great research papers [1, 2], review papers [3], books [4, 5, 6, 7, 8], and even websites.

Much of the literature focuses on polynomials as the de facto starting point. While this leads to deep connections between many fields within mathematics, and many applications in various areas (optimal control, data science, etc.), the need for arguably non-natural hierarchies (at least for beginners) sometimes makes the exposition hard to follow at first, and notations a tiny bit cumbersome.

I think that one reason is the aim for generality of the approaches. If you want to minimize potentially arbitrary continuous functions on a set defined by arbitrary equality or inequality constraints, there is not much choice if you want a unique generic mathematical framework that can approximate all of these problems. But if you are willing to optimize an arbitrary continuous function only on a “simple” set, then things considerably simplify: most results have explicit reasonably simple proofs, and you can even prove the exponential convergence of the SOS hierarchy! The main goal of this post is to present such old and recent results.

One other aim is to highlight the classical dual view of optimization problems through the characterization of probability measures by their moments, which has many applications beyond optimization.

By simple sets, I mean the interval \([0,\! 1]\) as a toy example, but by taking tensor products, this extends to the hypercube \([0,\! 1]^n\), and with a bit more work, you can add the Boolean hypercube \(\{-1,1\}^n\) and Euclidean spheres (see below). The key property that we will need is the availability of a nice orthonormal basis of square integrable functions.

Minimization of quadratic forms

In order to cover all cases, I will consider a generic minimization problem, $$\min_{x \in \mathcal{X}} \ f(x),$$ where \(\mathcal{X}\) is a compact set, e.g., \([0,\! 1]^n\) or \(\{-1,+1\}^n\) (I will use \([0,\! 1]\) as a running example). I will also first assume that the function \(f: \mathcal{X} \to \mathbb{R}\) can be represented as a quadratic form in some complex vector-valued feature \(\varphi: \mathcal{X} \to \mathbb{C}^d\), that is, there exists a Hermitian matrix \(F \in \mathbb{C}^{d \times d}\) (i.e., such that \(F^\ast = F\), where \(F^\ast\) is the “conjugate-transpose” of the matrix \(F\)), such that $$\forall x \in \mathcal{X}, \ f(x) = \varphi(x)^\ast F \varphi(x) = \sum_{j,k=1}^d \varphi_j(x) \varphi_k(x)^\ast F_{jk}.$$ I will also assume that features are normalized, that is, \(\| \varphi(x)\| = 1\) for all \(x \in \mathcal{X}\). Thus, the constant function equal to one is represented by the identity matrix.

For our running example, with \(\mathcal{X} = [0,\! 1]\), we can consider the Fourier basis $$\varphi_\omega(x) = \frac{1}{\sqrt{2r+1}} e^{2i\pi \omega x}, \ \ \omega \in \{-r,-r+1,\dots,r-1,r\}, $$ and then the assumption on \(f\) is that it is a real-valued linear combination of complex exponentials \(x \mapsto e^{2i\pi \omega x}\), for \(\omega \in \{-2r,-2r+1,\dots,2r-1,2r\}\), and thus a trigonometric polynomial of degree \(2r\) (that is a real bivariate polynomial of degree \(2r\) in \(\cos(2\pi x)\) and \(\sin(2\pi x)\)).

We see immediately in this example, that the representation of \(f\) through \(F\) is not unique. This is due to the fact that in the real vector space of Hermitian matrices of dimension \(d\), the rank-one matrices \( \varphi(x) \varphi(x)^\ast\) may only occupy a specific linear subspace, which we denote \(\mathcal{V}\). For the specific case of univariate trigonometric polynomials, we have $$(\varphi(x) \varphi(x)^\ast)_{\omega\omega’} = \frac{1}{{2r+1}} e^{2i\pi (\omega\, -\, \omega’) x},$$ so that the set \(\mathcal{V}\) is exactly the set of Hermitian Toeplitz matrices (which are constant along all diagonals), and thus a strict subset of all Hermitian matrices.

We will often use the trace trick to represent a quadratic form as a linear form in \(\varphi(x) \varphi(x)^\ast\), that is, $$ \varphi(x)^\ast F \varphi(x) = {\rm tr} \big[ F \varphi(x) \varphi(x)^\ast \big].$$ The set of matrices \(F\) that represent the function \(f\) exactly is an affine subspace orthogonal to \(\mathcal{V}\), that is, of the form \(F + \mathcal{V}^\perp\), where \(\mathcal{V}^\perp\) is the orthogonal of \(\mathcal{V}\) in the set of Hermitian matrices equipped with the dot-product \((M,N) \mapsto {\rm tr}(MN)\). For our running example, \(\mathcal{V}\) has dimension \(4r+1\), and hence its orthogonal has dimension \((2r+1)^2-4r-1 = 4r^2\).

Two dual convex views

The minimization of \(f\) has two dual convex optimization formulations, which are both natural, and which both provide insights into the problems.

Maximizing lower bounds. The first view is simply maximizing a lower bound on \(f\), that is, $$\min_{x \in \mathcal{X}} f(x) = \max_{c \in \mathbb{R}} \ c \ \mbox{ such that }\ \forall x \in \mathcal{X}, f(x)\, – c \geqslant 0.$$ The optimal \(c\) is then \(\min_{x \in \mathcal{X}} f(x)\). See an illustration below.

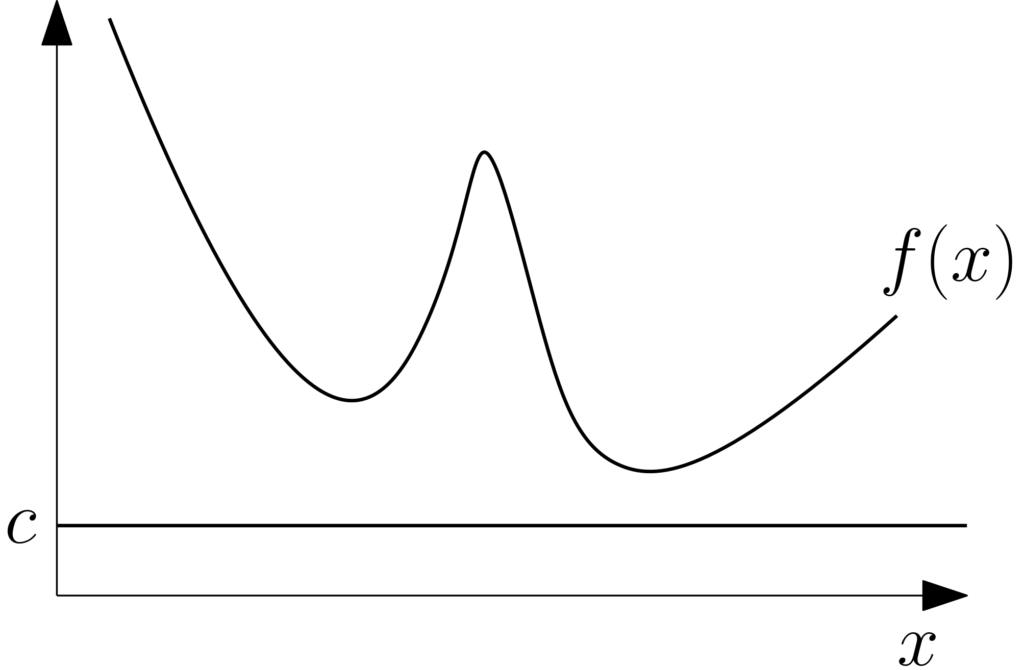
As mentioned in an earlier post, all optimization problems are thus convex! The hard computational task here is to represent efficiently non-negative functions to handle the (convex) constraint that \(f – c\) is non-negative.

Mininimizing expectations. The second view is looking for a probability measure \(\mu\) on \(\mathcal{X}\) with minimal expectation \(\int_\mathcal{X} \! f(x) d\mu(x)\). Denoting \(\mathcal{P}(\mathcal{X})\) the set of probability distributions on \(\mathcal{X}\), we have: $$\min_{x \in \mathcal{X}} f(x) = \min_{ \mu \in \mathcal{P}(\mathcal{X})} \int_\mathcal{X} f(x) d\mu(x),$$ and the minimizer is any probability measure supported on the minimizers of \(f\).

When \(f\) can be represented by a quadratic form, then the objective function becomes \(\displaystyle {\rm tr} \Big[ F\! \int_\mathcal{X} \varphi(x)\varphi(x)^\ast d\mu(x) \Big]\), which is linear in the moment matrix $$\Sigma = \int_\mathcal{X} \varphi(x)\varphi(x)^\ast d\mu(x).$$ The hard computational task is to represent efficiently the set of allowed moment matrices, which happens to be the closure of the convex hull \(\mathcal{K}\) of all \( \varphi(x) \varphi(x)^\ast\), \(x \in \mathcal{X}\) (remember that \(\mathcal{V}\) defined above is its linear span and thus contains \(\mathcal{K}\)). See an illustration below.

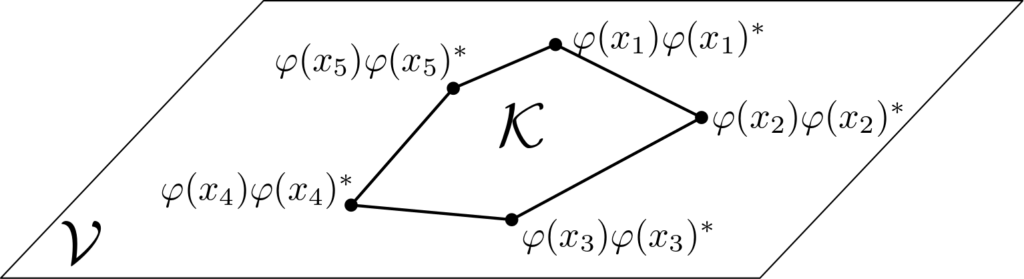
A key computational task will be to find outer approximations of \(\mathcal{K}\) based in particular on the knowledge of \(\mathcal{V}\).

Equivalence by convex duality. The two views are equivalent as one can see \(\mu\) as the Lagrange multiplier for the constraint \(\forall x \in \mathcal{X}, f(x)\, – c \geqslant 0\), which has to be a finite positive measure [10]. The Lagrangian is $$\mathcal{L}(c,\mu) = c + \int_\mathcal{X} ( f(x) \, – c) d\mu(x),$$ and minimizing with respect to the primal variable \(c\) leads to the constraint \(\int_\mathcal{X} d\mu(x) = 1\), that is, \(\mu\) is a probability distribution. Note that the traditional complementary slackness condition imposes that the optimal measure \(\mu\) puts mass only on minimizers of \(f\).

Convex relaxation: the sum-of-squares (SOS) view

A natural idea to characterize non-negative functions represented as quadratic forms is to consider positive-semidefinite (PSD) Hermitian matrices, that is, Hermitian matrices with non-negative eigenvalues. Indeed, if \(g(x) = \varphi(x)^\ast G \varphi(x)\) with \(G \succcurlyeq 0\) (which is another notation for \(G\) PSD), then \(g(x) \geqslant 0\) for all \(x \in \mathcal{X}\). This leads to the relaxation: $$\tag{1} \max_{c \in \mathbb{R}, \ A \in \mathbb{C}^{d \times d}} \ c \ \mbox{ such that } \ \forall x \in \mathcal{X}, \ f(x) = c + \varphi(x)^\ast A \varphi(x), \ A \succcurlyeq 0,$$ which is always lower than the minimal value of \(f\) since we replace non-negativity of \(f-c\) by a stronger sufficient condition. This is called an SOS relaxation because when \(G \succcurlyeq 0\), we can write \(g(x) = \varphi(x)^\ast G \varphi(x)\) as the sum of the squares of the functions \(x \mapsto \lambda_i^{1/2} u_i^\ast \varphi(x)\), where \(\lambda_i\) is the \(i\)-th (non-negative real) eigenvalue of \(G\), and \(u_i \in \mathbb{C}^d\) the corresponding eigenvector.

We can write the equality constraint compactly as (using that features have unit norm): $$ \forall x \in \mathcal{X}, \ \varphi(x)^\ast [ F – c I – A ] \varphi(x) = 0 \ \ \Leftrightarrow \ \ F – c I – A \in \mathcal{V}^\perp.$$ Using a variable \(-Y\) for an element of \(\mathcal{V}^\perp\) and eliminating \(A\), we get a constraint \(F + Y \succcurlyeq cI \), leading to \(c\) being the lowest eigenvalue of \(F +Y\) at optimum. This leads to a particularly simple formula for the relaxation: $$\tag{2} \max_{Y \in \mathcal{V}^\perp} \ \lambda_{\min} ( F + Y ).$$

The relaxation is tight for all \(F\), if and only if all non-negative functions represented as quadratic forms are SOS. This is not the case in general, and the relaxation is thus not tight in general, except in a few cases like uni-dimensional trigonometric polynomials.

It is tempting to set \(Y = 0\), and consider \(\lambda_{\min}(F)\), which is directly a lower-bound on the minimal value of \(f\), because, since features have been assumed to have unit norm, $$\lambda_{\min}(F) \ =\ \min_{ \| z\|=1} z^\ast F z\ \leqslant\ \min_{x \in \mathcal{X}} \ \varphi(x)^\ast F \varphi(x).$$ This is the classical spectral relaxation, which is much simpler than the SOS relaxation and can already lead to interesting behaviors. Note that we can see problem \((2)\) as the spectral relaxation optimized over all matrices \(F + Y\) that define the same quadratic form in \(\varphi(x)\).

Before looking at the performance of such relaxations, let’s first look at the dual view.

Convex relaxation: the moment view

Given that the objective function is linear in \( \varphi(x) \varphi(x)^\ast\), a traditional approach is to find outer approximations of the convex set \(\mathcal{K}\). The least we can expect from an outer approximation is that the affine hull is preserved, that is, we want to make sure that a matrix \(\Sigma\) in our approximation satisfies \(\Sigma \in \mathcal{V}\) (that is, Toeplitz for the trigonometric polynomial case), and \({\rm tr }(\Sigma) = 1\) (coming from \({\rm tr}(\varphi(x)\varphi(x)^\ast) = \| \varphi(x)\|^2 = 1\)).

Another natural property of the matrices \( \varphi(x) \varphi(x)^\ast\) is that they are positive semi-definite (PSD). The moment relaxation will exactly be the combination of these two properties (affine hull + PSD), leading to the outer approximation $$\widehat{\mathcal{K}} = \big\{ \Sigma \in \mathcal{V}, \ {\rm tr}(\Sigma)=1, \ \Sigma \succcurlyeq 0 \big\},$$ and to the relaxation $$\tag{3} \min_{ \Sigma \in \mathbb{C}^{d \times d}} \ {\rm tr} [ F \Sigma ] \ \mbox{ such that } \ \Sigma \succcurlyeq 0, \ {\rm tr}( \Sigma) = 1, \ \Sigma \in \mathcal{V}.$$

Removing the constraint that \(\Sigma \in \mathcal{V}\), we obtain again the (weaker) spectral relaxation.

Note that the outer approximation of \(\mathcal{K}\) by \(\widehat{\mathcal{K}}\) has many applications beyond optimization (see, e.g., [4, 7]). We get a tight relaxation for all \(F\), if and only if \(\mathcal{K}= \widehat{\mathcal{K}}\), which happens only in a few cases.

Equivalence by convex duality

By introducing the same Lagrange multiplier \(\mu\) which is now a signed measure (since we have an equality constraint), we obtain the Lagrangian $$\mathcal{L}(c,A, \mu) = c + \int_\mathcal{X} \big( f(x) \, – c \, – \, \varphi(x)^\ast A \varphi(x)\big) d\mu(x),$$ and minimizing with respect to \(c\) leads to the constraint \(\int_\mathcal{X} d\mu(x) = 1\), while optimizing with respect to \(A\) leads to the constraint \( \int_\mathcal{X} \varphi(x)\varphi(x)^\ast d\mu(x) \succcurlyeq 0\), and we exactly get the moment relaxation by setting \(\Sigma = \int_\mathcal{X} \varphi(x)\varphi(x)^\ast d\mu(x)\). Another way of seeing it is that the two semidefinite programs \((2)\) and \((3)\) are dual to each other.

The two views are thus equivalent, and tightness of one is equivalent to the tightness of the other. We will see below that for our running example of univariate trigonometric polynomials, the relaxation is tight, before looking at the multivariate case, where the relaxation is not tight, but can be made as tight as desired. We will then allow infinite-dimensional feature maps by allowing infinitely many frequencies.

Let’s first mention a few “practicalities”: solving either \((2)\) or \((3)\) with efficient algorithms, and obtaining a candidate minimizer from a moment matrix \(\Sigma\).

Convex optimization algorithms. Standard interior point methods for semi-definite programming problems can be used for either \((2)\) or \((3)\). This will become slow when the dimension \(d\) of the feature map \(\varphi(x)\) gets large, as each iteration will be of complexity \(O(d^3)\). Moreover, encoding the vector space \(\mathcal{V}\) can be rather painful when \(\mathcal{X}\) has many dimensions. For efficient descriptions of \(\mathcal{V}\) based on sampling, see the kernel section below. For efficient algorithms based on smoothing the minimal eigenvalue, see the bottom of the post.

Recovering a minimizer. This is often referred to as “extraction” in the SOS literature [29], and a variety of techniques exist. Note also that randomized techniques which are classical in combinatorial optimization can also be considered [30].

Univariate trigonometric polynomials

We first start with the SOS view, by showing that all non-negative trigonometric polynomials are sums-of-squares, and here a single square.

Fejér-Riesz theorem [11, 12] (if you can read German). We consider a trigonometric polynomial of degree \(r\), that is, \(g(x) = \sum_{\omega = -r}^r c_\omega e^{2i\pi \omega x}\) with real non-negative values. This imposes that \(c_{-\omega} = c_\omega^\ast\). Then it is non-negative if and only if it can be written as the square modulus of a complex-valued trigonometric polynomial. The elementary proof based on roots of polynomials is shown at the end of the post.

We here get a single square, with an elementary proof. Note that this is a stronger result than being a sum of several squares. We can now look at the dual intepretation.

Positivity of Hermitian Toeplitz matrices. As mentioned earlier, our approximation set \(\widehat{\mathcal{K}}\) for \(\mathcal{K}\) is the set of PSD Toeplitz matrices of unit trace. We have a tight relaxation if we can show that for any such matrix \(\Sigma\), there exists a probability measure \(\mu\) on \([0,\! 1]\) such that $$ \Sigma_{\omega\omega’}= \int_{0}^1 e^{2 i \pi (\omega \, -\, \omega’)x} d\mu(x)$$ for all \(\omega,\omega’\). This is a classical result in Toeplitz matrix theory, from [13] (if you read German), well summarized in [14].

Comparison with spectral relaxation. Assume we are given a trigonometric polynomial of degree \(2r\), that is, \(f(x) = \sum_{\omega = -2r}^{2r} c_\omega e^{2i\pi \omega x}\). As mentioned earlier, there are many ways of representing it as a quadratic form \(\varphi(x)^\ast F \varphi(x)\) with \(\varphi(x)_\omega = e^{2i\pi \omega x}/\sqrt{2r+1}\) for \(\omega \in \{-r,\dots,r\}\). This will not change the SOS relaxation but will make a difference for the spectral relaxation. One standard one is to choose \(F\) to be a Toeplitz matrix. Since \(F_{\omega\omega’}\) should depend only on \(\omega-\omega’\), by counting the number of elements in each diagonal, we must have $$\tag{4} F_{\omega \omega’} = c_{\omega\, -\, \omega’} \frac{2r+1}{2r+1-|\omega\, -\, \omega’|}= c_{\omega\, -\, \omega’} \frac{1}{1-|\omega\, -\, \omega’|/(2r+1)}.$$

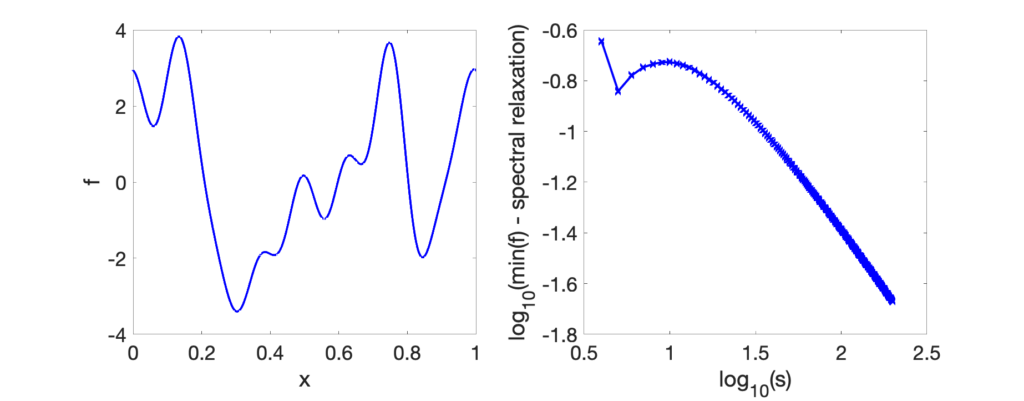
The spectral relaxation amounts to compute the lowest eigenvalue of a Toeplitz matrix, which is a well studied problem [9], in particular when the dimension of the matrix grows. In our context, this corresponds to considering a feature \(\varphi\) of size \(s\) larger than \(r\) (like we will do for multivariate polynomials below), representing the function \(f\) in this basis through a Toeplitz matrix \(F\) of size \((2s+1)\times(2s+1)\) with the same formula as \((4)\), and seeing how the spectral relaxation tends to the optimal value when \(s\) goes to infinity.

We first consider the Toeplitz matrices with values \(c_{\omega-\omega’}1_{|\omega-\omega’|\leqslant 2r}\) for \(|\omega|, |\omega’| \leqslant s\), which is, a band-diagonal Toeplitz matrix. it is shown in [31, Section 5.4] that the lowest eigenvalue of this Toeplitz matrix has the following asymptotic expansion \(f(x_\ast) + \frac{f^{\prime\prime}(x_\ast)}{32 s^2}\) where \(x_\ast \in [0,\! 1]\) is the minimizer of \(f\) (assumed to be unique). We thus get an upper approximation of \(O(1/s^2)\). By taking into account the multiplicative factor \(\frac{1}{1-|\omega-\omega’|/(2s+1)}\) from Eq. \((4)\), we get an overall factor of \(O(1/s)\), which is what we observe in practice (see simple experiment below).

The spectral relaxation is convergent, but much slower than the SOS relaxation (which is tight for \(r\geqslant s\)).

Consequences for regular polynomials on \([-1,1]\). Non-negative polynomials \(P\) on \([-1,1]\) can also be characterized, by looking at the non-negativity of \(f(x) = P(\cos 2 \pi x)\) for \(x \in [0,\! 1]\), which is equivalent to the existence of a complex trigonometric polynomial whose square modulus is exactly \(f\). Playing around with Chebyshev polynomials of the two kinds, one can show that \(P(y)\) then has to a sum of terms of the form \(Q(y)^2 + (1-y^2) R(y)^2\), where \(Q\) and \(R\) are polynomials, which is the classical SOS characterization of non-negative polynomials in \([-1,1]\) [15]. See all details and the extension to higher dimensions in [33].

Extension to multivariate trigonometric polynomials

We now consider multivariate trigonometric polynomials in dimension \(n\), on \([0,\! 1]^n\), which are polynomials in \(\cos 2\pi x_1, \sin 2\pi x_1, \dots, \cos 2\pi x_n, \sin 2 \pi x_n\). We first start with a counter-example to the equivalence between non-negativity and being a sum of squares.

Negative result (counter-example). Non-negative polynomials may not be sums-of-squares, as shown by this counter example based on Motzkin’s example [22]: $$M(1-\cos 2 \pi x_1,1-\cos 2\pi x_2, 1 – \cos 2 \pi x_3)$$ $$\mbox{ with } M(y_1,y_2,y_3) = y_1^2 y_2 + y_1 y_2^2 + y_3^3 \, – 3 y_1 y_2 y_3.$$ It is non-negative as (up to a factor of \(1/3\)) the difference between the arithmetic and geometric mean of \(y_1^2 y_2\), \(y_1 y_2^2\), and \(y_3^3\), and not a sum of squares. Note that to check that \(f\) is not a sum-of-squares of polynomials of a given degree, we can solve an SDP and look at the smallest \(c \geqslant 0\) such that \(f + c\) is a sum-of-squares, and check that the optimal \(c\) is strictly greater than zero (we here obtain \(c \approx 1.1 \times 10^{-4}\) for degree \(2\) polynomials). It is a bit more involved to show that there is no SOS polynomials of any degree (cancellation of terms are possible so the degree can be higher than the one of \(f\)), see [22].

So not all non-negative polynomials are sums-of-squares in dimension larger than 1. This is however not the end of the story, as we now describe.

Towards positive results. We consider a trigonometric polynomial, that is, a function \(f(x) = P(e^{2i\pi x_1},\dots,e^{2i\pi x_n})\) where \(P\) is a function of the form $$P(z) = \sum_{ \omega \in \mathbb{Z}^d} c_\omega z^\omega, $$ where only a finite number of \(c_\omega\)’s are not equal to zero (we use the notation \(z^\omega = \prod_{i=1}^n z_i^{\omega_i}\)). Like in the one-dimensional case, the function \(f\) is real-valued as soon as \(c_{-\omega} = c_\omega^\ast\) for all \(\omega \in \mathbb{Z}^n\). These are exactly multivariate (real-valued) trigonometric polynomials.

We now state a few results relating non-negativity and sums-of-squares, whose “elementary” proofs will either be sketched at the end of this post (below references) or available in [33].

Strictly positive polynomials are sums-of-squares. For any multivariate trigonometric polynomial \(f\) of the form above, if \(f\) is strictly positive on \([0,\! 1]^n\), then there exists a finite family of trigonometric polynomials \((g_i)_{i \in I}\) such that $$ \forall x \in [0,\! 1]^n, \ f(x) = \sum_{i \in I} |g_i(x)|^2.$$ This result dates back to [28], and has a reasonably simple proof based on Bochner’s theorem (see at the bottom of the post the proof from [23]).

There are two key deviations from the univariate case:

1. The degrees of the squares \(|g_i|^2\) can be larger than the degree of \(f\) and are not bounded a priori, thus, we need to try sums of squares of degrees larger than the degree of \(f\), thus creating a hierarchy of optimization problems of higher dimensions, whose optimal value will converge to the minimum of \(f\).
2. Only strictly positive polynomials can always be decomposed, implying we may not have finite convergence of the hierarchy in general.

It implies that SOS hierarchies will always converge to the true value, without giving any idea of the convergence rate. The next result provides such a result (but still quite pessimistic), without any assumption.

Adding an arbitrarily small constant to a non-negative trigonometric polynomial makes it an SOS of known degree. Given a multivariate trigonometric polynomial of degree less than \(2r\) with values in \([0,\! 1]\), \(f + c\) is a sum of squares of polynomials of degree less than \(s \geqslant r\) as soon as \(c \geqslant c^\ast(r,s)\) for some \(c^\ast(r,s)\). Moreover, when \(s \to +\infty\), we have recently shown in [33] that, asymptotically, \(c^\ast(r,s) \leqslant \frac{6 r^2 n}{s^2} \sum_{\omega \in \mathbb{Z}^n} | \hat{f}(\omega)|\). This immediately provides the convergence rate \(c^\ast(r,s)\) for the SOS relaxation of degree \(s\).

This results in an adaptation of [20] to \([0,\! 1]^n\) rather than the hypersphere, which makes the proof significantly faster (see [33] and the related results for regular polynomials on \([-1,1]^n\) in [34]). It provides a quantitative guarantee (even more explicit than for regular polynomials [26]): the approximation guarantee scales as \(s^{-2}\), with a feature dimension \(d = (2s+1)^n \sim s^n\), and thus with a feature of dimension \(d\), we get an error proportional to \(d^{-2/n}\), thus with a scaling in the underlying dimension \(n\) subject to the curse of dimensionality.

Comparison with spectral relaxation. Using the same reasoning as in dimension \(n=1\), we get instead a convergence rate in \(O(1/s)\) for the spectral algorithm. So we get convergence, at rate which is only slightly worse. However, the behavior in \(O(1/s)\) is empirically observed in practice in all cases, while the rate in \(O(1/s^2)\) for the SOS relaxation is pessimistic, and the convergence rate is much better in practice. Can we obtain tighter convergence rates?

Exponential convergence

In order to show exponential convergence when the degree \(s\) goes to infinity, we need to add an extra assumption regarding the behavior of the function \(f\) around its minimizer. Essentially, all global minimizers are isolated and the Hessian is invertible. This is often referred to as “strict-second-order minimizers”, and such assumptions have already been used to show finite convergence of the hierarchy, although with no bound on the required degree [35].

Leveraging our earlier work [21, 24], we recently showed in [33] with Alessandro Rudi that the convergence rate was exponential when the minimum is attained at isolated points with invertible Hessians. The proof is a bit involved, but rely on a crucial point. We deviate from previous work on polynomial hierarchies by a strong focus on smoothness properties of the optimization problems rather than its algebraic properties. More precisely, this allows us to use square roots and matrix square roots together with their differentiability properties (square roots typically lead to non-polynomial functions when taken on polynomials).

Optimization beyond trigonometric polynomials

When \(f\) is not a trigonometric polynomial, there are essentially two options: (1) approximate with a trigonometric polynomial and minimize the approximation with the SOS hierarchy, or (2) target directly the minimization of the original function through sampling. The second option is described in the next section (and was already the topic of an earlier blog post). We now describe the first option.

Approximation by truncated Fourier series. Depending on how the function is accessed, through function values or through values of its Fourier series, the approximation of a regular function \(f\) through a degree \(r\) polynomial is a well-studied problem. For simplicity, I only consider truncating the Fourier series obtained by keeping frequencies \(\omega\) such that \(\| \omega\|_\infty \leqslant r\). The error which is made depends on the regularity of the original function, that is, if \(f\) has all of its \((\beta + n)\)-th order derivatives that are bounded, then the truncation error is of order \(1/r^{\beta}\). Thus, to reach precision \(\varepsilon\), we need \(d \sim r^n \sim \varepsilon^{-n/\beta}\) basis functions. See an illustration below in two dimensions, where aim to approximate the function below.

The function is approximated by computing the Fourier series and keeping only frequencies \(\omega\) such that \(\| \omega \|_\infty \leqslant r\) for varying \(r\).

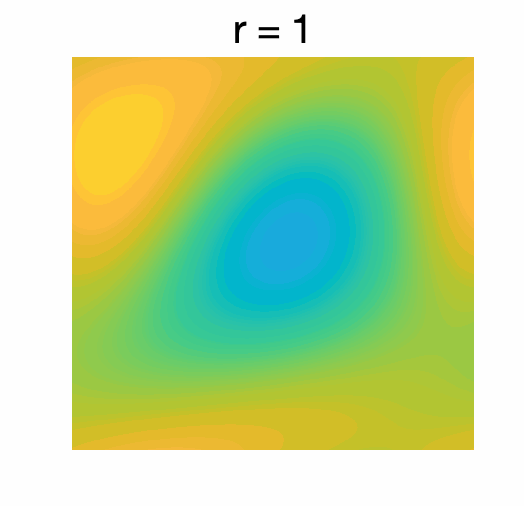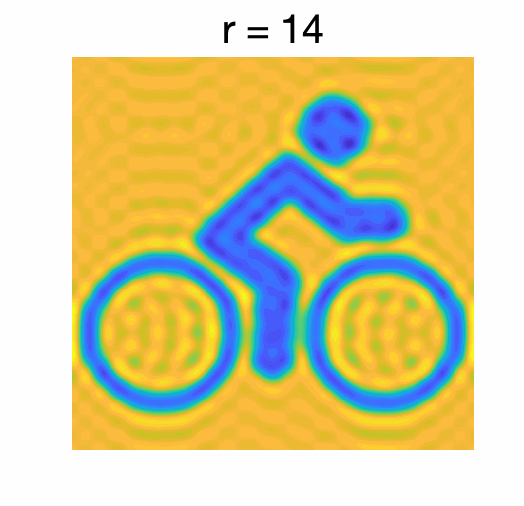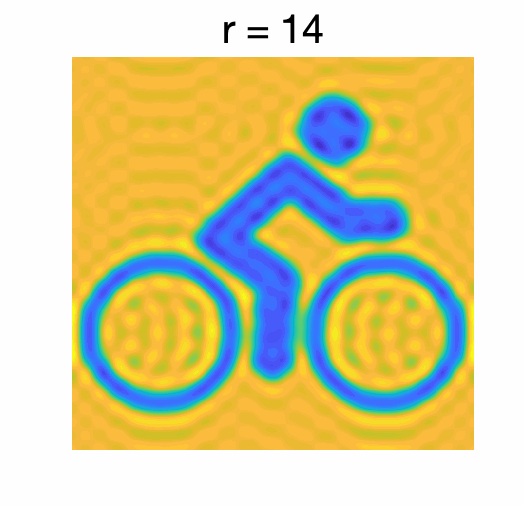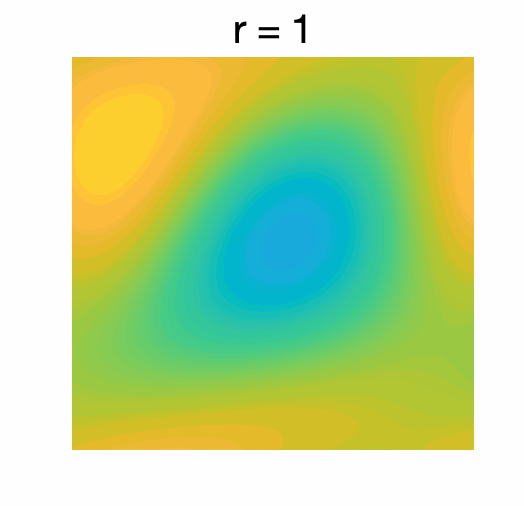
Extension to function value oracle

Now that the traditional “décor” of sum-of-squares optimization based on finite-dimensional expansions has been set, we can look at recent infinite-dimensional extensions based on positive definite kernels.

From knowing \(\mathcal{V}\) to exact sampling. In the formulation above, instead of using an explicit representation of \(f(x)\) as \(\varphi(x)^\ast F \varphi(x)\), and determine precisely \(\mathcal{V}\), an alternative is to use sufficiently many distinct points \(x_1,\dots,x_m \in \mathcal{X}\), and use the constraint: $$ \forall i \in \{1,\dots,m\}, \ f(x_i) -c = \varphi(x_i)^\ast A \varphi(x_i). $$ If the matrices \(\varphi(x_i) \varphi(x_i)^\ast\), \(i \in \{1,\dots,m\}\), span \(\mathcal{V}\), this is equivalent to the original formulation [25], and leads to formulations that are less cumbersome to code (multivariate Toeplitz matrices are an example). An extra advantage is to access \(f\) only through a function-value oracle (often called a zero-th order oracle). Note that we often need to take \(m\) larger than the dimension \(2d\) (the real dimension of \(\mathbb{C}^d\)), but always less than \(d^2\) (the real dimension of the set of Hermitian matrices).

Undersampling and regularization. A key insight from [21] is to consider situations where the number of samples \( m\) is not large enough, and add a regularizer \( -\lambda {\rm tr}(A)\), that is, $$ \sup_{c \in \mathbb{R}, \ A \succcurlyeq 0} c\, – \lambda {\rm tr}(A) \  \mbox{ such that } \ \forall i \in \{1,\dots,m\}, \ f(x_i) -c = \varphi(x_i)^\ast A \varphi(x_i).$$ The dual is then: $$ \inf_{\alpha \in \mathbb{R}^m} \sum_{i=1}^m \alpha_i f(x_i) \mbox{ such that } \sum_{i=1}^m \alpha_i = 1, \ \sum_{i=1}^m \alpha_i \varphi(x_i)\varphi(x_i)^\ast + \lambda I \succcurlyeq 0. $$

When \( m\) is large enough and \( \lambda\) is sufficiently small, this leads to a controlled approximation. This is particularly interesting when \(\varphi(x)\) is infinite-dimensional and such that the relaxation is tight, which we now look at.

Infinite-dimensional feature map. In the trigonometric polynomial example, we can consider $$\varphi(x)_\omega = \hat{q}(\omega)^{1/2} e^{2i \pi \omega^\top x},$$ with an extra weight function \(\hat{q}: \mathbb{Z}^n \to \mathbb{R}_+\), such that \(\sum_{\omega \in \mathbb{Z}^n} \hat{q}(\omega) = 1\), so that \(\| \varphi(x)\| = 1\) (we essentially get a probability distribution on \(\mathbb{Z}^n\)). Finite-dimensional embeddings correspond to \(\hat{q}\) having finite support, but we can now to apply the SOS technique in infinite dimensions, since \(\hat{q}\) may have infinitely many non-zero values.

Tightness. A key benefit of going infinite-dimensional is that the SOS relaxation is always tight as soon as \(\hat{q}(\omega) >0\) for all \(\omega \in \mathbb{Z}^d\). Indeed, the relaxation is the following optimization problem: $$\inf_{ \mu \ {\rm finite \ measure} } \int_{\mathcal{X}} f(x) d\mu(x) \ \mbox{ such that } \ \int_{\mathcal{X}} \varphi(x)\varphi(x)^\ast d\mu(x) \succcurlyeq 0, \ \int_\mathcal{X} d\mu(x) = 1.$$ Looking at all finite sub-matrices of \(\int_{\mathcal{X}} \varphi(x)\varphi(x)^\ast d\mu(x)\), we see that the function \(\omega \mapsto \int_{[0, 1]^n} e^{2i\pi \omega^\top x} d\mu(x)\) is positive definite, and thus by Bochner’s theorem, \(\mu\) has to be a probability measure.

We can now combine with “sampling + regularization” technique mentioned above, and only query the function at a finite number of points. As shown in [21, 24], with a proper choice of \(\lambda\), then we get a convergence rate of \(O(1/m^{-\beta/n})\) when \(f\) is \((\beta + 2+ n/2)\)-times differentiable. When \(f\) is infinitely-differentiable (like for functions with finite support), we can get exponential convergence in \(m\), but with a constant in from of the exponential that can be exponential in dimension. See more details in an earlier blog post and in [33].

Representer theorem. Another consequence is a “representer theorem”, that is, we can reduce the search to \(A = \sum_{i,j=1}^m C_{ij} \varphi(x_i)\varphi(x_j)^\ast\) with \( C \in \mathbb{R}^{m \times m}\) positive-semidefinite. Like for traditional kernel methods, the representer theorem is particularly interesting when \(d\) is infinite like above.

But this is already useful with finite-dimensional embeddings where the span \(\mathcal{V}\) is difficult to characterize. In this case, only the kernel has to be simple to compute; for example, for the usual finite support case, we have $$k(x,y) = \frac{1}{2r+1} \frac{ \sin (2r+1) \pi x }{\sin \pi x},$$ in one dimension (this extends to all dimensions). We can also get a closed form for \(\hat{q}(\omega) = \rho^{\|\omega\|_1}\).

Extension to Boolean hypercube

When \(\mathcal{X} = \{-1,1\}^n \), we can use feature vectors composed of Boolean Fourier components of increasing orders [16]. This corresponds to features of the form \(\varphi_A(x) = \prod_{i \in A} x_i \in \{-1,1\}\), where \(A\) is a subset of \(\{1,\dots,n\}\). They are all normalized.

If we consider a set \( \mathcal{A}\) of subsets of \( \{1,\dots,n\}\), then, the element indexed \((A,B)\) of \(\varphi(x) \varphi(x)^\ast\) only depends on the symmetric difference \(A \Delta B = ( A \backslash B) \cup ( B \backslash A)\). The relaxation is not tight in general, but if we see our moment matrix as a submatrix obtained from a sufficiently larger set of subsets, then we obtain a tight formulation (here we know that the hierarchy has to be finite [17, 18, 19]).

At the first layer (with \( \mathcal{A}\) composed of singletons), we get the traditional semi-definite programming relaxation of quadratic optimization problems on \(\{-1,1\}^n\) [30]. See this nice website for the many extensions. An interesting aspect is that tightness is not necessary in many applications.

Extension to hyperspheres

It is common to see the set \([0,\! 1]\) with periodic functions as the one-dimensional torus, that is, the quotient set \(\mathbb{R} / \mathbb{Z}\). Another classical interpretation is to see it as the unit circle in \(\mathbb{R}^2\), with the bijection \(x \mapsto (\cos 2\pi x, \sin 2 \pi x)\). The real Fourier basis functions \(x \mapsto \cos 2 \pi \omega x\) and \(x \mapsto \sin 2 \pi \omega x\) are then polynomials \(P(y_1,y_2)\) in \(y_1 = \cos 2\pi x\) and \(y_2 = \sin 2\pi x\). Not all polynomials are recovered, as one can check that we need to have \(\Delta P = \frac{\partial^2 P}{\partial y_1^2} + \frac{\partial^2 P}{\partial y_2^2}=0\), that is the Laplacian of \(P\) is zero, which is often referred to as being harmonic. This extends to hyperspheres in any dimension (see [20] for details), and also to Euclidean balls by adding a dimension.

Conclusion

In this blog post, I have tried to describe the basics of sums-of-squares optimization, hopefully from a simple perspective. The key was to reduce the scope to the minimization over simple sets with no complex constraints. This allowed us to present significantly improved convergence results from [33].

There is of course many more interesting ideas to cover, such as constrained optimisation, applications within signal processing [8], and extensions to the computation of log-partition functions [32], as well as important practical scalability issues to alleviate. Moreover, the SOS framework goes beyond optimization, either through other infinite-dimensional optimization problems or moment-based formulations (see many examples in [4, 7]). Many topics for future posts!

Acknowledgements. I would like to thank Alessandro Rudi for proofreading this blog post and making good clarifying suggestions.

 

References

[1] Jean-Bernard Lasserre. Global optimization with polynomials and the problem of moments. SIAM Journal on Optimization, 11(3):796–817, 2001.
[2] Pablo A. Parrilo. Semidefinite programming relaxations for semialgebraic problems. Mathematical Programming, 96(2):293–320, 2003.
[3] Monique Laurent. Sums of squares, moment matrices and optimization over polynomials. In Emerging applications of algebraic geometry. Springer, 157-270, 2009.
[4] Jean-Bernard Lasserre. Moments, positive polynomials and their applications. World Scientific, 2009.
[5] Grigoriy Blekherman, Pablo A. Parrilo, Rekha R. Thomas, editors. Semidefinite optimization and convex algebraic geometry. Society for Industrial and Applied Mathematics, 2012.
[6] Jean-Bernard Lasserre. An introduction to polynomial and semi-algebraic optimization. Cambridge University Press, 2015.
[7] Didier Henrion, Milan Korda, and Jean-Bernard Lasserre. The Moment-SOS Hierarchy: Lectures In Probability, Statistics, Computational Geometry, Control And Nonlinear PDEs. World Scientific, 2020.
[8] Bogdan Dumitrescu. Positive trigonometric polynomials and signal processing applications. Springer, 2007.
[9] Robert M. Gray. Toeplitz and circulant matrices: A review. Foundations and Trends in Communications and Information Theory 2(3): 155-239, 2006.
[10] Johannes Jahn. Introduction to the Theory of Nonlinear Optimization. Springer, 2020
[11] Leopold Fejér. Über trigonometrische Polynome. Journal für die reine und angewandte Mathematik. 146:55-82, 1916.
[12] Friedrich Riesz. Über ein Problem des Herrn Carathéodory. Journal für die reine und angewandte Mathematik. 146:83-87, 1916.
[13] C. Carathéodory and L. Fejér. Über den Zusammenhang der Extreme von harmonischen Funktionen mit ihren Koeffizienten und über den Picard-Landauschen Satz, Rendiconti del Circolo Matematico di Palermo, 32:218–239, 1911.
[14] Mihály Bakonyi, Ekaterina V. Lopushanskaya. Moment problems for real measures on the unit circle. Recent Advances in Operator Theory in Hilbert and Krein Spaces. Birkhäuser Basel, 49-60, 2009.
[15] Victoria Powers and Bruce Reznick. Polynomials that are positive on an interval. Transactions of the American Mathematical Society, 352(10):4677–4692, 2000.
[16] Ryan O’Donnell. Analysis of Boolean functions. Cambridge University Press, 2014.
[17] Jean-Bernard Lasserre. An explicit exact SDP relaxation for nonlinear 0–1 programs. In International Conference on Integer Programming and Combinatorial Optimization, pages 293–303. Springer, 2001.
[18] Monique Laurent. A comparison of the Sherali-Adams, Lovász-Schrijver, and Lasserre relaxations for 0–1 programming. Mathematics of Operations Research, 28(3):470–496, 2003.
[19] Lucas Slot and Monique Laurent. Sum-of-squares hierarchies for binary polynomial optimization. Mathematical Programming, pages 1–40, 2022.
[20] Kun Fang and Hamza Fawzi. The sum-of-squares hierarchy on the sphere and applications in quantum information theory. Mathematical Programming, 190(1):331–360, 2021.
[21] Alessandro Rudi, Ulysse Marteau-Ferey, Francis Bach. Finding Global Minima via Kernel Approximations. Technical report arXiv:2012.11978, 2020.
[22] Aron Naftalevich, and M. Schreiber. Trigonometric polynomials and sums of squares. In Number Theory. Springer, 225-238, 1985.
[23] Alexandre Megretski. Positivity of trigonometric polynomials. In International Conference on Decision and Control, 2003.
[24] Blake Woodworth, Francis Bach, Alessandro Rudi. Non-Convex Optimization with Certificates and Fast Rates Through Kernel Sums of Squares. In Proceedings of the Conference on Learning Theory, 2022.
[25] Diego Cifuentes, Pablo A. Parrilo. Sampling algebraic varieties for sum of squares programs. SIAM Journal on Optimization, 27(4): 2381-2404, 2017.
[26] Jean-Bernard Lasserre. A sum of squares approximation of nonnegative polynomials. SIAM Review, 49(4):651-669, 2007.
[27] Yurii Nesterov. Smoothing technique and its applications in semidefinite optimization. Mathematical Programming 110(2):245-259, 2007.
[28] Mihai Putinar. Sur la complexification du problème des moments. Comptes Rendus de l’Académie des Sciences, Série 1, Mathématique 314(10):743-745, 1992.
[29] Didier Henrion and Jean-Bernard Lasserre. Detecting global optimality and extracting solutions in GloptiPoly. In Positive polynomials in control, pages 293-310, 2005.
[30] Michel X. Goemans and David P. Williamson. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. Journal of the ACM, 42(6):1115–1145, 1995.
[31] Ulf Grenander, and Gabor Szegö. Toeplitz forms and their applications. Univ of California Press, 1958.
[32] Francis Bach. Sum-of-Squares Relaxations for Information Theory and Variational Inference. Technical report, arXiv:2206.13285, 2022.
[33] Francis Bach and Alessandro Rudi. Exponential convergence of sum-of-squares hierarchies for trigonometric polynomials. Technical report arXiv:2211.04889, 2022.
[34] Monique Laurent and Lucas Slot. An effective version of Schmüdgen’s Positivstellensatz for the hypercube. Optimization Letters, 2022.
[35] Jiawang Nie. Optimality conditions and finite convergence of Lasserre’s hierarchy. Mathematical Programming, 146(1):97–121, 2014

Proof of Fejér-Riesz theorem

We consider a trigonometric polynomial of degree \(r\), that is, \(g(x) = \sum_{\omega = -r}^r c_\omega e^{2i\pi \omega x}\) with real non-negative values. This imposes that \(c_{-\omega} = c_\omega^\ast\). We assume that \(c_r \neq 0\). We consider the rational function \(R(z) = \sum_{\omega = -r}^r c_\omega z^\omega\), so that \(g(x) = R(e^{2i\pi x})\). We can write \(R\) as \(R(z) = z^{-r} Q(z)\) for a polynomial \(Q\) of degree \(2r\). We can now examine the roots of \(R\). The identity \(c_{-\omega} = c_\omega^\ast\) implies that if \(z\) is a root of \(Q\), so is \(1/z^\ast\). Thus all roots which do not have unit modulus come in pairs \((z_b,1/z_b^\ast)\), for \(| z_b| < 1\), with \(b \in \{1,\dots,m\}\). We then have \(2r \, – 2m\) roots of unit modulus, denoted \(e^{2i\pi \rho_a}\), for \(a \in \{1,\dots,2r-2m\}\).

Thus, we can write the polynomial \(Q\) as: $$Q(z) = \kappa \prod_{a=1}^{2r-2m} ( z \, – e^{2i\pi \rho_a}) \prod_{b = 1}^m ( z \, – z_b)( z \, – 1/z_b^\ast), $$ for a certain \(\kappa \in \mathbb{C}\), leading to $$R(z) = z^{-r} Q(z) = \kappa’ z^{-r+m} \prod_{a=1}^{2r-2m} ( z \, – e^{2i\pi \rho_a}) \prod_{b =1}^m ( z \, – z_b)( z^{-1} \, – z_b^\ast),$$ for some \(\kappa’ \in \mathbb{C}\). For \(z = e^{2i\pi x}\), the second product is a positive number since \(z^{-1} = z^\ast\). Writing \( e^{2i\pi x} \, – e^{2i\pi \rho_a} = 2i e^{i\pi(x+\rho_a)} \sin \pi (x-\rho_a)\), we can see that in order to avoid a change of sign of \(\sin \pi (x-\rho_a)\) around some \(x\), each \(\rho_a\) must appear with even multiplicity. Thus, for \(z = e^{2i\pi x}\), the term \(z^{-r+m} \prod_{a=1}^{2r-2m} ( z \, – e^{2i\pi \rho_a})\) is equal to \(\prod_{a=1}^{r-m} (-4) e^{2 i\pi \rho_a} \sin^2 \pi (x-\rho_a)\), and thus, \(\kappa^{\prime\prime} = \kappa’ \prod_{a=1}^{r-m} (-4) e^{2 i\pi \rho_a}\) has to be a non-negative real number. Thus, overall, $$g(x) = R(e^{2i\pi x}) = \Big| \sqrt{\kappa^{\prime\prime}} \prod_{a=1}^r ( e^{2i\pi x} – e^{2i\pi \rho_a}) \prod_{b =1}^m ( e^{2i\pi x} – z_b) \Big|^2.$$

We here get a single square, with an elementary proof. Note that this is a stronger result than being a sum of several squares. We can now look at the dual intepretation.

First-order algorithms

In order to solve the problem in Eq. \((1)\), we can use standard smoothing [27], that is, replace \(\lambda_{\min}(F+Y)\) by \(\varepsilon \log {\rm tr } \exp((F+Y) / \varepsilon)\), and apply accelerated projected gradient descent, which requires to orthogonally project on \(\mathcal{V}^\perp\), or equivalently on \(\mathcal{V}^\perp\).

All strictly positive trigonometric polynomials are sums-of-squares

In order to provide an “elementary” proof of this result that dates back to [28], we follow [23] and proceed by contradiction, and assume that there is a strictly positive trigonometric polynomial \(R\) which is not a sum-of-squares. Since the set of SOS polynomials is a convex cone, by the Hahn-Banach theorem, there must exist a non identically zero linear form \(L\) which is non-negative on all SOS polynomials, and such that \(L(R) \leqslant 0\). In order to conclude, we will need to show that linear forms on trigonometric polynomials that are non-negative on SOS polynomials, can be written as $$\tag{4} L(P) = \int_{[0, 1]^n} P(e^{ 2i\pi x_1} ,\dots, e^{2i\pi x_n}) d\mu(x)$$ for a non-negative measure \(\mu\) on \([0,\! 1]^n\) (which is not uniformly equal to zero). This then leads to a contradiction, since it implies $$0 \geqslant L(R) \geqslant \min_{x \in [0, 1]^n} R(e^{ 2i\pi x_1} ,\dots, e^{2i\pi x_n}) \times \mu([0,\! 1]^n).$$

We now need to show that all bounded linear forms on trigonometric polynomials that are non-negative on SOS polynomials can be represented as in Eq. \((4)\).

Using Bochner’s theorem. We define a function \(g: \mathbb{Z}^n \to \mathbb{C}\) as \(g(\omega) = L( z^\omega)\). This function is positive definite, as, for any \(\omega_1,\dots,\omega_m \in \mathbb{Z}^n\) and any complex numbers \(\alpha_1,\dots,\alpha_m\), $$ \sum_{i,j=1}^m \alpha_i \alpha_j^\ast g(\omega_i – \omega_j) = L \Big( \Big| \sum_{i=1}^m \alpha_i z^{\omega_i} \Big|^2 \Big).$$ Thus by Bochner’s theorem, there exists a positive measure \(\mu\) on \([0,\! 1]^n\) such that $$g(\omega) = \int_{[0, 1]^n} e^{2i\pi \omega^\top x} d\mu(x),$$ which exactly leads to the desired result.