The “η-trick” reloaded: multiple kernel learning

In my previous post, I described various (potentially non-smooth) functions that have quadratic (and thus smooth) variational formulations, a possibility that I referred to as the η-trick. For example, in its simplest formulation, we have $ \displaystyle |w| = \min_{ \eta \geq 0} \frac{1}{2} \frac{w^2}{\eta} + \frac{1}{2} \eta$.

While it seems most often used for deriving simple optimization algorithms, it has other applications and interpretations in machine learning, in particular for “multiple kernel learning” (MKL), super-Gaussian distributions and convex relaxations of combinatorial penalties. In this post, I will cover the MKL part, which leads to a framework for learning discriminative representations from data.

We first take a detour through supervised learning with linear models based on features.

Learning “features” for “linear” predictions

Consider the typical supervised learning problem of estimating labels $y_i \in \mathbb{R}$ from some inputs $x_i$ in a input space $\mathcal{X}$, for $i = 1,\dots,n$. The input space $\mathcal{X}$ is left generic on purpose, and, both in theory and practice, inputs can have a wide variety of structures (e.g., images, sequences, graphs, web pages, text documents, logs, etc.).

In order to deal with such potentially non-vectorial inputs, a feature map $\varphi: \mathcal{X} \to \mathbb{R}^d$ is often used, and then linear models consider prediction functions of the form $f(x) = w^\top \varphi(x)$, where $w \in \mathbb{R}^d$ is a weight vector. The terminology “linear” refers to linearity in the parameters $w$, and not linearity in the inputs $x$; indeed, $\varphi$ may be non-linear, and the notion can even have no meaning if $\mathcal{X}$ is not a vector space (note that when $\mathcal{X} = \mathbb{R}^d$, and $\varphi(x) = x$, which is common in many applications, we have in this particular situation predictions that are linear in the inputs). Given the feature map $\varphi$, the first task is to learn the parameter vector $w \in \mathbb{R}^d$.

Using the square loss for simplicity (but everything extends to convex loss functions such as the logistic loss), training is usually done by minimizing with respect to $w$ the so-called regularized empirical risk $$ \frac{1}{2n} \sum_{i=1}^n \big(y_i – w^\top \varphi(x_i) \big)^2 + \frac{\lambda}{2} \| w\|_2^2,$$ where the $\ell_2$-norm-regularization is standard to avoid overfitting and makes the problem numerically well-behaved. While for general convex loss functions, we would get a convex optimization problem, here, with the square loss, it is even simpler as we can get a solution in closed form (see below).

While explicit fixed feature maps $\varphi : \mathcal{X} \to \mathbb{R}^d$ have always been successfully used, learning these feature maps directly from data is an important task in machine learning. Given some parameterization $\varphi_\eta(x)$ (with parameters $\eta$), one then minimizes the objective function $$ \frac{1}{2n} \sum_{i=1}^n \big(y_i – w^\top \varphi_\eta(x_i) \big)^2 + \frac{\lambda}{2} \| w \|_2^2,$$ both with respect to the weight vector $w$ and the feature parameters $\eta$ (the only change from the equation above is the replacement of $\varphi(x_i)$ by $\varphi_\eta(x_i)$). Regardless of the particular parametrization of $\varphi_\eta$, the optimization problem is convex in $w$, but typically is not convex in $\eta$ (and even more rarely jointly convex).

This framework includes (but is not limited to) neural networks, where $w$ is the set of output weights and $\eta$ corresponds to all other neuron weights, and $\varphi_\eta(x)$ is the value of the last hidden layer; see an example below.

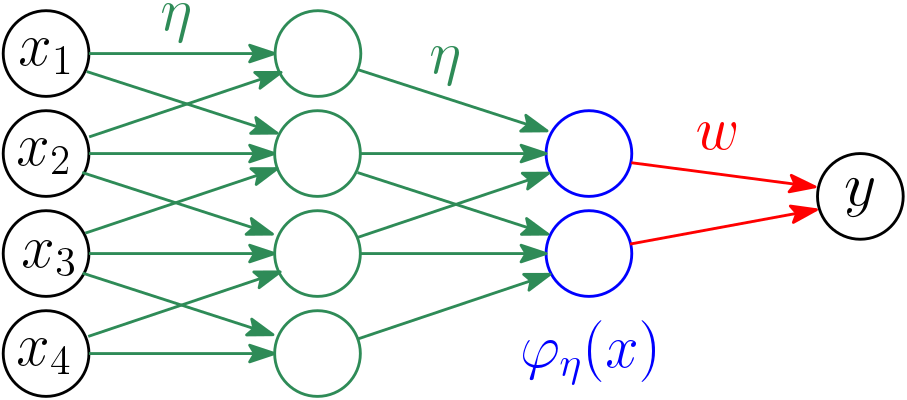
Neural networks with two hidden layers. The input weights $\eta$ (in green) define a function $x \mapsto \varphi_\eta(x)$, which is the last hidden layer (in blue), which can be linearly combined with output weights $w$ (in red), leading to the output $y$.

The most direct approach is to estimate $(\eta,w)$ through joint gradient descent techniques. For neural networks, the problem is not jointly convex in $(\eta,w)$, but remains convex in $w$; thus, even if $\eta$ is not optimally estimated, the optimization in $w$ by gradient descent, which is robust (since the objective function is convex), can still lead to a good prediction function $x \mapsto w^\top \varphi_\eta(x)$ (in particular when the size of the feature vector $d$ is large). In other words (and in a quite intuitive/hand-wavy way), being very precise in the feature vector $\varphi_\eta$ (which we cannot guarantee) is not as important as being precise in optimizing $w$ (which we can). A key empirical property of (deep) neural networks is that, with the proper initialization and stochastic gradient descent algorithms, the feature parameters $\eta$ can be learned with sufficient precision and great adaptivity to the final task (of predicting the labels). The theory about this now well-known empirical behavior is starting to emerge (a topic for another post).

Another approach to learn parameters, which comes with theoretical guarantees because it relies on a jointly convex problem when using appropriate parameterizations, is to first minimize with respect to $w$ (again, which is easy because of convexity), and optimize the resulting function with respect to the feature map $\varphi_\eta$. It turns out that there is a nice connection with kernel methods, as I now show.

Optimizing the weight vector $w$ and the kernel trick

We consider a generic feature map $\varphi_\eta: \mathcal{X} \to \mathbb{R}^d$, and we denote by $\Phi \in \mathbb{R}^{n \times d}$ the concatenation of all $n$ feature vectors $\varphi_\eta(x_i)$, $i=1,\dots,n$ (since we consider $\eta$ fixed in this section, we drop the dependence in $\eta$). the objective writes in compact form $$ \frac{1}{2n} \| y – \Phi w \|_2^2 + \frac{\lambda}{2} \| w\|_2^2.$$ Its gradient is equal to $\frac{1}{n} \Phi ^\top ( \Phi w – y ) + \lambda w$, and setting it to zero leads to the minimizer $w = ( \Phi ^\top \Phi + n \lambda I)^{-1} \Phi^\top y \in \mathbb{R}^d$.

We can then use the matrix inversion lemma, to obtain $w = \Phi^\top ( \Phi \Phi ^\top + n \lambda I)^{-1} y$. By doing so we went from the empirical (non-centered) covariance matrix $\frac{1}{n} \Phi ^\top \Phi \in \mathbb{R}^{d \times d}$ of the features, to the kernel matrix $K = \Phi \Phi^\top \in \mathbb{R}^{n \times n}$. The notation $\alpha = ( \Phi \Phi^\top + n \lambda I)^{-1} y = ( K + n \lambda I)^{-1} y \in \mathbb{R}^n$ is often used, so that $w = \Phi^\top \alpha = \sum_{i=1}^n \alpha_i \varphi_\eta(x_i)$, that is, $w$ is a linear combination of the input features and the weights in this combination can be computed by only accessing the input features through the kernel matrix, which is composed of dot-products $\varphi_\eta(x_i)^\top \varphi_\eta(x_j)$. This is exactly the kernel trick and (an explicit version of) the representer theorem.

The kernel trick allows to work with large feature spaces, i.e., feature maps $\varphi$ with potentially high (and sometimes infinite) output dimension $d$, with a computational cost which is independent of $d$, if the kernel $k(x,x’) = \varphi_\eta(x)^\top \varphi_\eta(x’)$ can be evaluated cheaply. Such kernels have been designed in the last twenty years for most of the common data types that I mentioned above (e.g., images, sequences, graphs, web pages, text documents, logs, etc.). See, e.g., the two reference books [1] and [2], as well as the nice teaching slides of Jean-Philippe Vert.

Note that kernel methods unfortunately come naturally with a running time with a quadratic dependence in $n$ (as this is the cost of computing the kernel matrix), unless specific techniques are used (Nyström / column sampling or random features) to have a running-time which is subquadratic in $n$ (these will be topics for future posts).

Convexity of the optimized objective

Now that we can compute the minimizer of the optimization problem above in closed form $w = ( \Phi^\top \Phi+ n \lambda I)^{-1} \Phi^\top y$, we can evaluate the optimal value of the objective $$ \frac{1}{2n} \| y – \Phi w \|_2^2 + \frac{\lambda}{2} \| w\|_2^2 = \frac{1}{2n} y^\top y \ – \frac{1}{n} y^\top \Phi w + \frac{1}{2n} w^\top ( \Phi^\top \Phi + n \lambda I) w . $$ This leads to after replacing $w$ by its value, $$ \frac{1}{2n} y^\top y \ – \frac{1}{2n} y^\top \Phi ( \Phi^\top \Phi+ n \lambda I)^{-1} \Phi^\top y = \frac{1}{2n} y^\top \big( I – \Phi ( \Phi^\top \Phi+ n \lambda I)^{-1} \Phi^\top\big) y.$$ Using the matrix inversion lemma again, the optimized objective is equal to $$\frac{1}{2n} y^\top \big( I – ( \Phi \Phi^\top + n \lambda I)^{-1} \Phi \Phi^\top\big) y = \frac{1}{2n} y^\top \big( I – ( K + n \lambda I)^{-1} K \big) y = \frac{\lambda}{2} y^\top ( K + n \lambda I)^{-1} y. $$

The features only enter this optimal value as a function $R(K)$ of the kernel matrix $K = \Phi \Phi^\top \in \mathbb{R}^{n \times n}$. This function happens to be convex, which can be seen here from the explicit expression of $R(K)$ and a bit of knowledge in convex analysis (see the classical Boyd and Vandenberghe book, example 3.4). This is true beyond the square loss and this can nicely be obtained by Lagrange duality (see [3]).

As I now present, this convexity is the source of approaches to learn the kernel matrix (and hence implicitly the feature vectors) directly from data.

Multiple kernel learning (MKL)

Given that the set of kernel matrices is a convex cone, a natural parameterization is through a conic combination $K(\eta) = \sum_{j=1}^m \eta_j K^j$ of base kernel matrices $K^1,\dots,K^m$, with $\eta \in \mathbb{R}^m$ being a vector of positive weights. The typical application scenario is as follows: for a given type of data (e.g., images or biological sequences), several kernel functions $k^1,\dots,k^m : \mathcal{X} \times \mathcal{X} \to \mathbb{R}$ exist in the literature, based on different principles and types of information. Combining them allows to benefit from the predictive power of all of them. This framework is referred to as multiple kernel learning.

Typically, a regularization constraint on the trace of the kernel matrix $K(\eta)$ is used as the trace of the kernel matrix is known to be a good quantity to control generalization to unseen data (see [3]); this leads to a (positive) linear constraint on the vector $\eta$.

It turns out that there is a nice relationship with sparsity-inducing norms, which is obtained through the η-trick. We first reinterpret the problem as follows: we consider the feature maps $\varphi^j: \mathcal{X} \to \mathbb{R}^{d_j}$ associated with each kernel $k^j$, $j=1,\dots,m$, so that $K^j_{a,b} = \varphi^j(x_a)^\top \varphi^j(x_b)$ for all $a,b \in {1,\dots,n}$. We can then consider the weighted concatenated feature map $$\varphi_\eta(x) = ( \eta_1^{1/2} \varphi^1(x), \dots, \eta_m^{1/2} \varphi^m(x)) \in \mathbb{R}^{d_1+\dots+d_m},$$ for which the kernel $\varphi_\eta(x)^\top \varphi_\eta(x’) $ is equal to $\sum_{j=1}^m \eta_j k^j(x,x’)$. See a representation below.

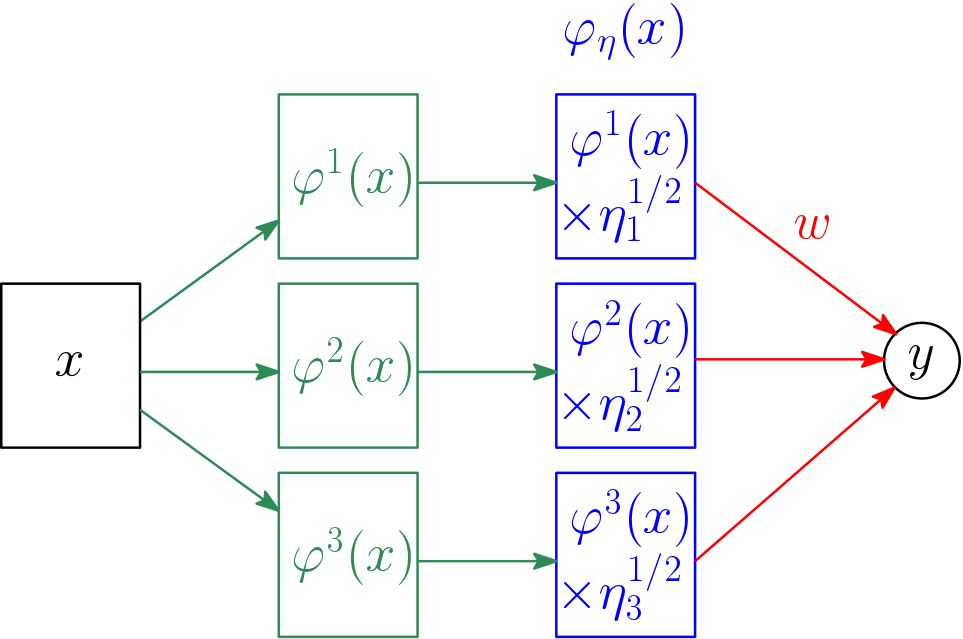
Multiple kernel learning with three blocks of features (in green), multiplied by the kernel parameters $\eta_1,\eta_2,\eta_3$ to obtain the weighted concatenated feature vector $\varphi_\eta(x)$ (in blue), composed of three blocks. Note that all blocks are typically multi-dimensional. These last blue blocks are linearly combined with weights $w$ (in red), leading to the output $y$.

This provides a link between weighted sums of kernel matrices and specifically parameterized feature maps: we can indeed see the problem either as estimating a specific feature vector $\varphi_\eta$, or as estimating a conic combination of matrices. The key benefit of this formulation is that it is jointly convex in $(w,\eta)$, and thus provably “easy” to optimize.

The η-trick provides an interesting link with sparsity-inducing norms.

Equivalence with group Lasso

We consider as above $m$ block of features and we denote by $\Phi^j \in \mathbb{R}^{n \times d_j}$ the design matrix for the block $j \in \{1,\dots,m\}$. The (squared) group Lasso problem aims at estimating a linear combination of each block of variables with a regularization term that selects whole blocks (instead of individual variables regardless of the block structures if an $\ell_1$-norm was used): $$ \min_{ v_1 \in \mathbb{R}^{d_1}, \dots, \ v_m \in \mathbb{R}^{d_m}} \frac{1}{2n} \| y – \Phi^1 v_1 – \cdots – \Phi^m v_m \|_2^2 + \frac{\lambda}{2} \Big( \| v_1\|_2 + \cdots + \| v_m\|_2 \Big)^2.$$

We can apply the η-trick to obtain the equivalent problem: $$ \min_{ v_1 \in \mathbb{R}^{d_1}, \dots, \ v_m \in \mathbb{R}^{d_m}} \min_{ \eta \in \Delta_m} \frac{1}{2n} \| y – \Phi^1 v_1 – \cdots – \Phi^m v_m \|_2^2 + \frac{\lambda}{2} \Big( \frac{\| v_1\|_2^2}{\eta_1} + \cdots + \frac{ \| v_m\|_2^2}{\eta_m} \Big),$$ where $\Delta_m$ is the simplex in $\mathbb{R}^m$. Using the change of variable $w_j = \eta_j^{-1/2} v_j$, we exactly get the minimization of $$ \frac{1}{2n} \| y – \Phi_\eta {w} \|^2 + \frac{\lambda}{2} \| {w} \|_2^2,$$ where $\Phi_\eta \in \mathbb{R}^{n \times (d_1+\cdots+d_m)}$ is the design matrix associated with the concatenated weighted features $\varphi_\eta(x_i)$, $i=1,\dots,n$.

Applying our results above, we can minimize with respect to ${w}$ in closed form as ${w} = ( \Phi_\eta^\top \Phi_\eta + n \lambda I)^{-1} \Phi_\eta^\top y$, and the resulting minimization problem in $\eta$ becomes $$ \min_{\eta \in \Delta_m} \frac{\lambda}{2} y^\top \big( K(\eta) + n \lambda I \big)^{-1} y,$$ where $K(\eta) = \sum_{j=1}^m \eta_j \Phi^j (\Phi^j)^\top \in \mathbb{R}^{n \times n}$ is a kernel matrix which is a convex combination of the $m$ kernel matrices $K^j = \Phi^j (\Phi^j)^\top$ corresponding to each block of input variables.

Thus, the group Lasso is equivalent to optimizing over kernel matrices of the form $K(\eta)$ the convex function $R: K \mapsto \frac{\lambda}{2} y^\top ( K + n \lambda I )^{-1} y$, which happens to be exactly the minimal value of the kernel ridge regression problem, that is, the regularized training error after training that we have presented above (note here that in order to have the constraint that $\eta$ is on the simplex, that is, $\eta_1+\cdots + \eta_m = 1$, we can simply impose that all kernel matrices, including $K(\eta)$, have the same trace, which is standard in practice).

NB: This equivalence between group Lasso and MKL was first proved by Gert Lanckriet, Michael Jordan and myself [4], using convex duality and a less intuitive argument, while Alain Rakotomamonjy, Stéphane Canu, Yves Grandvalet and myself [5] used the η-trick as described above (if you know about earlier references, please let me know).

Consequences and extensions

The equivalence between MKL and group Lasso has several interesting consequences.

Learning weights or using uniform weights: through the η-trick, we can thus see that minimizing the regularized training error with respect to the kernel matrix is in fact the solution of a sparsity-inducing formulation. Thus it should only be used when such behavior is expected, i.e., learning from a large set of kernel matrices $K^j$, and selecting only a few of them (for theoretical guarantees, see [6]). If all kernel matrices are well-selected by the practitioner, a uniform sum typically suffices. In particular, note that for our feature weighting parametrization, the space of functions $x \mapsto w^\top \varphi_\eta(x)$ when $w$ varies is always the same as soon as all components of $\eta$ are strictly positive, and thus using learned or uniform weights should correspond to a prior knowledge that one has about the particular set of kernel matrices.
Algorithms for MKL / group Lasso: Since the optimization problem is jointly convex in $(w,\eta)$, the global optimum can be found with arbitrary precision, with a variety of algorithms, working with kernels or not; see [7, section 1.5].

This equivalence has several interesting extensions beyond plain sparsity or group sparsity.

Beyond conic combinations: Other parameterizations of kernel matrices can be used, some of them related to the extension of the η-trick which I mention in my previous post. For example, when using $K(\Lambda) = \Phi \Lambda \Phi^\top$ where $\Lambda$ is a symmetric positive semidefinite matrix, we obtain an equivalence with trace norm regularization [8].
Different constraints on η‘s: The trace penalty leads to a linear constraint on top of positivity. Other constraints can be used, such as $\ell_p$-norms for $p \geq 1$ [9], or constraints that induce specific behaviors on the selection of blocks of variables [7, section 3.4], e.g., block $\Phi^1$ always has to be selected before block $\Phi^2$.

Learning features or kernels?

In conclusion, we have seen two main ways of estimating data representations directly from data, which seem different: learning an explicit feature representation (often called an “embedding”) $\varphi_\eta(x)$ or the corresponding kernel $\varphi_\eta(x)^\top \varphi_\eta(x’)$, where features are only implicit. When using these representations through linear models (which is the standard way), using one or the other makes no difference in predictive performance, but usually it does on algorithms required to learn on these features, which may need one representation or the others.

For stochastic gradient based algorithms, using explicit $d$-dimensional representations leads to algorithms whose running-time complexity is proportional to $nd$, which, when $d$ is small, can be advantageous over the complexity in $O(n^2)$ associated with just computing the $n \times n$ kernel matrix. Therefore, explicit features numerically seem beneficial at first, but, specific techniques can be used (Nyström / column sampling or random features) to obtain a similar running time (again, to be explained in a future post). Thus, once appropriately done, going for features or kernels does not make a huge difference.

The parametrization of the feature vector $\varphi_\eta(x)$ or the associated kernel makes however a key difference. To obtain a jointly convex representation in $(w,\eta)$, we need a representation in terms of kernels which is linear in $\eta$, which is a significant modelling limitation: only feature reweighting is possible, which is already useful in presence of many such features. However, when non-linear feature building is required, more complex parametrizations are needed. Empirically, although leading to jointly non-convex problems, they have been used efficiently and successfully in a wide variety of neural networks. Providing theoretical guarantees and guidelines on how to achieve such non-linear feature learning is an active area of research.

References

[1] Bernhard Schölkopf et Alexander Smola. Learning with kernels, MIT Press, 2002.
[2] Nello Cristianini and John Shawe-Taylor. Kernel Methods for Pattern Analysis, Cambridge University Press, 2004.
[3] Gert R. Lanckriet, Nello Cristianini, Peter Bartlett, Laurent El Ghaoui, and Michael I. Jordan. Learning the kernel matrix with semidefinite programming. Journal of Machine learning research, 5:27-72, 2004.
[4] Francis Bach, Gert R. G. Lanckriet, Michael I. Jordan. Multiple Kernel Learning, Conic Duality, and the SMO Algorithm. Proceedings of the International Conference on Machine Learning (ICML), 2004.
[5] Alain Rakotomamonjy, Francis Bach, Stéphane Canu, and Yves Grandvalet. SimpleMKL. Journal of Machine Learning Research, 9:2491-2521, 2008.
[6] Francis Bach. Consistency of the group Lasso and multiple kernel learning. Journal of Machine Learning Research, 9:1179-1225, 2008.
[7] Francis Bach, Rodolphe Jenatton, Julien Mairal, Guillaume Obozinski. Optimization with sparsity-inducing penalties. Foundations and Trends in Machine Learning, 4(1):1-106, 2012.
[8] Andreas Argyriou, Theodoros Evgeniou, and Massimiliano Pontil. Multi-task feature learning. Advances in Neural Information Processing Systems (NIPS), 2007.
[9] Marius Kloft, Ulf Brefeld, Sören Sonnenburg, Alexander Zien. $\ell_p$-Norm Multiple Kernel Learning. Journal of Machine Learning Research, 12:953−997, 2011.