Playing with positive definite matrices – II: entropy edition

Symmetric positive semi-definite (PSD) matrices come up in a variety of places in machine learning, statistics, and optimization, and more generally in most domains of applied mathematics. When estimating or optimizing over the set of such matrices, several geometries can be used. The most direct one is to consider PSD matrices as a convex set in the vector space of all symmetric matrices and thus to inherit the Euclidean geometry. Like for the positive orthant (which corresponds to diagonal PSD matrices), this is not natural for a variety of reasons. In this post we will consider Bregman divergences to define our notion of geometry.

A first natural and common geometry is to consider PSD matrices as covariance matrices (or their inverses, often referred to a precision or concentration matrices). They can thus be seen as parameters of zero-mean Gaussian random vectors, and classical notions from information theory, such as the Kullback-Leibler divergence, can be brought to bear to define a specific geometry. This happens to be equivalent to using the negative log determinant to define the Bregman divergence, and leads to the usual Stein divergence $$ – \log \det A + \log \det B \ – {\rm tr}[ – B^{\, -1} ( A \, – B) ] = -\log \det (AB^{\, -1}) + {\rm tr}( A B^{\, -1}) \ – d, $$ which is the Kullback Leibler divergence between two Gaussian random vectors with zero means and covariance matrices \(B\) and \(A\).

In this blog post, we consider a different but related matrix function, which will be \(A \mapsto {\rm tr } [ A \log A]\) instead of \(– {\rm tr} [ \log A ]\). This will have stronger links with the Shannon entropy of discrete random variables [1]. In particular, we will be able to extend two classical notions related to discrete entropy:

• The entropy function \(H(p) = \ – \sum_{i=1}^d p_i \log p_i\), defined on the simplex \(\Delta \subset \mathbb{R}^d\) (vectors with non-negative components that sum to one), is concave, while the associated Bregman divergence, here the usual Kullback-Leibler (KL) divergence, is $$ \sum_{i=1}^d p_i \log \frac{p_i}{q_i}. $$ It is jointly convex in the vectors \(p\) and \(q\) (see this nice article [6] for other jointly convex Bregman divergences). Note that the joint convexity is here a direct application of classical results regarding the convexity of the perspective of a convex function [10, section 3.2.6].
• The Fenchel-Legendre conjugate of \(-H\) (with the simplex as domain) is $$\sup_{p \in \Delta} \ \ p^\top z\ – \sum_{i=1}^d p_i \log p_i = \log \Big( \sum_{i=1}^d \exp(z_i) \Big).$$ With the positive orthant as the domain, we have $$\sup_{p \in \mathbb{R}_+^d }\ \ p^\top z \ – \sum_{i=1}^d p_i \log p_i = \sum_{i=1}^d \exp(z_i-1) .$$ This has many consequences in probabilistic modelling, notably the duality between maximum likelihood and maximum entropy [1, 7].

The extension to matrices will have several interesting consequences:

• This defines a Bregman divergence that has interesting applications to mirror descent and smoothing techniques in optimization.
• The non-trivial joint convexity of the associated Bregman divergence will lead to elegant methods for deriving concentration inequalities for symmetric matrices [2].
• Application to covariance operators in infinite-dimensional spaces will lead to a whole range of information-theoretic results [5], but this is for next month!

Von Neumann entropy and relative entropy

Given a positive semi-definite symmetric matrix \(A \in \mathcal{S}_d\), the von Neumann entropy is defined as $$H(A) =\ – {\rm tr} [ A \log A],$$ as the trace of the matrix function \(– A \log A\), or equivalently as \(– \sum_{i=1}^d \! \lambda_i \log \lambda_i\) where \(\lambda_1,\dots,\lambda_d \geqslant 0\) are the \(d\) eigenvalues of \(A\) (note that we can have a zero eigenvalue and still be finite).

From last month blog post, we get that \(H\) is concave. We can then naturally define on the spectrahedron (set of positive semi-definite matrices with unit trace), the relative entropy, which is the Bregman divergence associated with the function \(A \mapsto {\rm tr} [ A \log A]\), whose gradient is \(\log A + I \), leading to: $$D(A\| B) = {\rm tr} [ A \log A ] \, – {\rm tr} [ B \log B] \, – {\rm tr} \big[ ( A \, – B) ( \log B + I ) \big],$$ which is equal to $$ D(A\| B) = {\rm tr} \big[ A ( \log A \, – \log B ) \big] – {\rm tr}(A) + {\rm tr}(B).$$ This time we have to be careful to avoid infinite values: it is finite if and only if the null space of \(B\) is included in the one of \(A\), or, equivalently if \(B^{\, -1/2} A^{1/2} B^{\, -1/2}\) is finite. Note that when \(A\) and \(B\) have unit traces, the term in \(– {\rm tr}(A) + {\rm tr}(B)\) goes away.

As a Bregman divergence of a strictly convex function, \(D(A\|B)\) is non-negative and equal to zero if and only if \(A = B\).

When \(A = {\rm Diag}(p)\) and \(B = {\rm Diag}(q)\) are diagonal, we get $$D(A\| B) = \sum_{i=1}^d \Big\{ p_i \log \frac{p_i}{q_i} \, – p_i + q_i \Big\},$$ and we recover the traditional relative entropy.

Please refrain from writing \(D(A\| B) = {\rm tr} \big[ A \log ( A B^{\,-1} ) \big] – {\rm tr}(A) + {\rm tr}(B)\), which is not true unless \(A\) and \(B\) commute. See however below how using Kronecker products can make a similar equality always true.

A geometry on matrices

The von Neumann relative entropy (also referred to as matrix KL divergence) defines a new notion of geometry, which is different from the Euclidean geometry based on the squared Frobenius norm \(\| A – B \|_{\rm F}^2 = {\rm tr} [ ( A -B)^2]\). Below, we plot and compare balls for these various geometries. We first consider Euclidean balls, defined as $$\mbox{ Euclidean : } \ \big\{ B \in \mathcal{S}_d, \| A – B \|_{\rm F}^2 \leqslant r \big\},$$ as well as the two KL balls (one for each side of the KL divergence): $$ \mbox{ Left KL : } \ \big\{ B \in \mathcal{S}_d, D(B\|A) \leqslant r \big\},$$ $$\mbox{ Right KL : } \big\{ B \in \mathcal{S}_d, D(A\|B) \leqslant r \big\}.$$

Diagonal matrices with unit trace (isomorphic to the simplex). We consider diagonal matrices \(A = {\rm Diag}(p)\) with \(p\) in the simplex. We compare the three balls below (in yellow), with \(r = 1/16\) for the three of them.

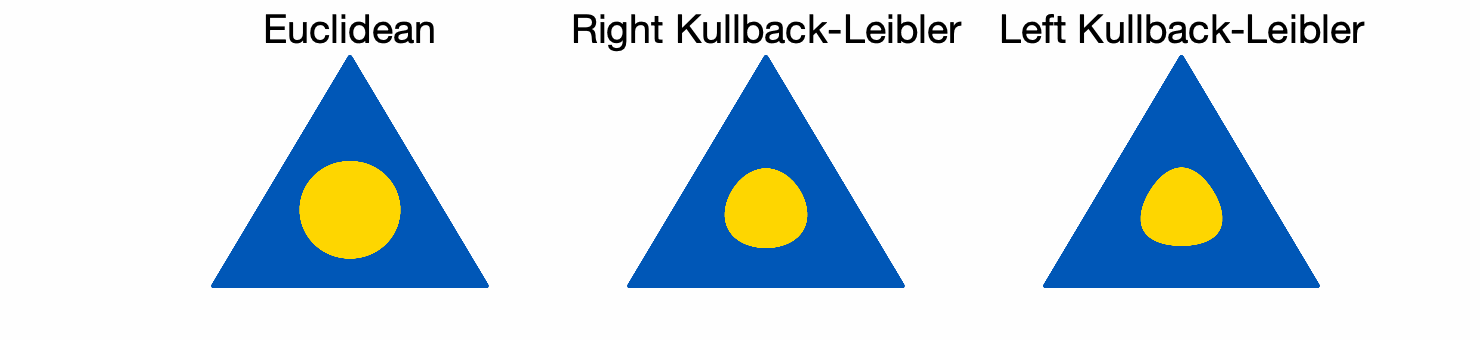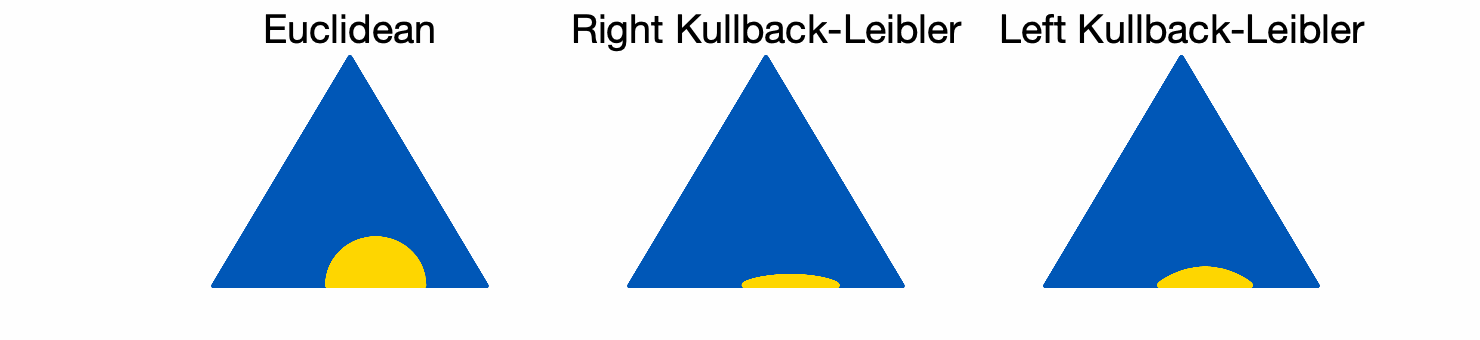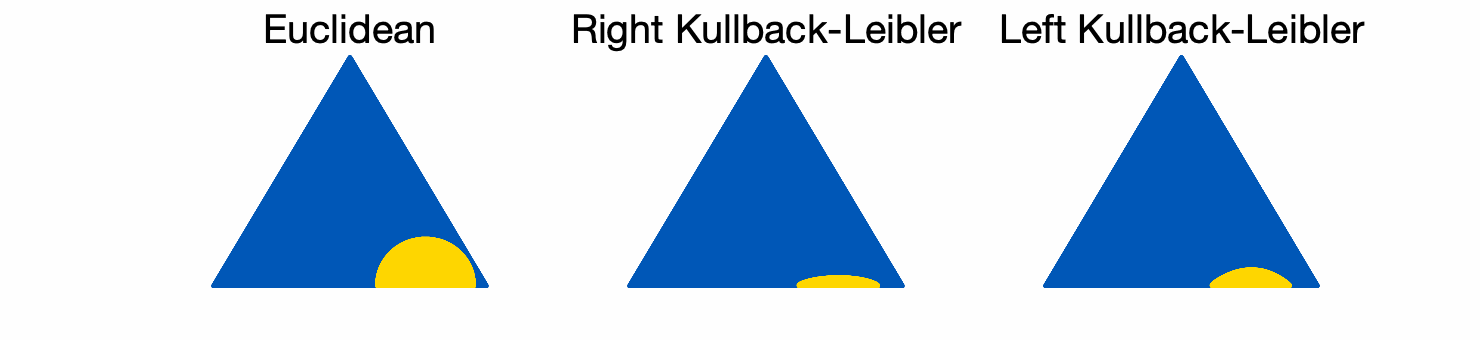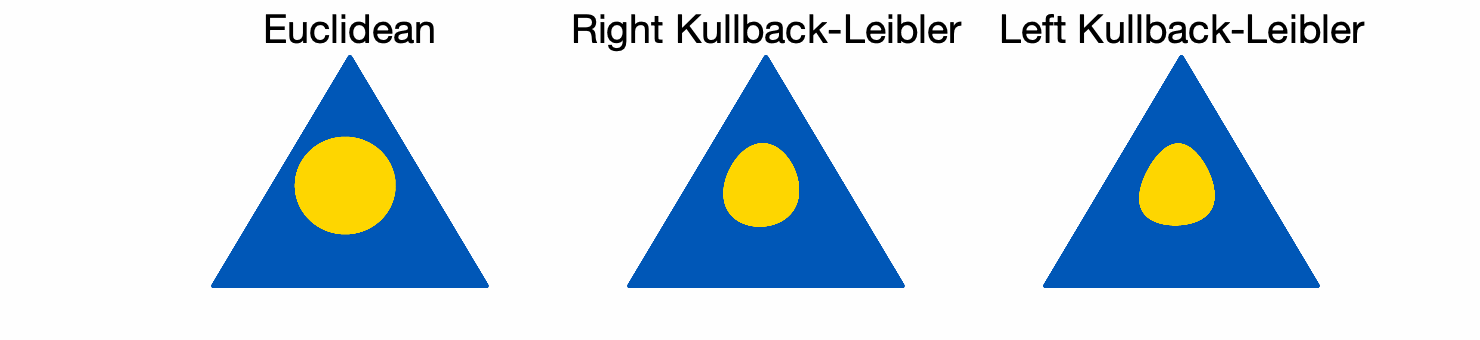
While the Euclidean balls have the same shapes at all positions, the KL balls adapt their shapes to their centers.

Unit trace PSD matrices in dimension two (isomorphic to the Euclidean ball). We consider matrices \(A = \Big( \begin{array}{cc} x & y \\[-.15cm] y & \!\!\!1-x\!\end{array} \Big)\) with the PSD constraint being equivalent to \(y^2 \leqslant x(1-x)\), that is, \((x,y)\) is in the disk of center \((\frac{1}{2},0)\) and radius \(\frac{1}{2}\). We compare the three balls below (in yellow), with \(r = \frac{1}{32}\) for the Euclidean ball, and \(r =\frac{1}{16}\) for the KL balls, with a similar difference between geometries.

Pinsker inequality

In order to use the relative entropy within mirror descent, we need an extension of the Pinsker inequality $$\sum_{i=1}^d p_i \log \frac{p_i}{q_i} \geqslant \frac{1}{2} \Big(\sum_{i=1}^d | p_i – q_i| \Big)^2,$$ which is, in optimization terms, the \(1\)-strong-concavity of the entropy with respect to the \(\ell_1\)-norm. It turns out that the natural extension is true, that is, for PSD matrices with unit trace, $$D(A\| B) = {\rm tr} \big[ A ( \log A\, – \log B ) \big] \geqslant \frac{1}{2} \| A \ – B \|_\ast^2,$$ where \(\| \cdot \|_\ast\) denotes the trace norm, a.k.a. the nuclear norm, that is, the \(\ell_1\)-norm of eigenvalues. See [3] for a nice and simple proof.

This allows to use the relative entropy when optimizing over the spectrahedron using mirror descent [11]. Note that the diameter \(\sup_{A} {\rm tr} [ A \log A] \ – \inf_{A} {\rm tr} [ A \log A] \) over PSD matrices with unit trace is equal to \(\log d\). Using duality, the relative entropy can also be used for smoothing the maximal eigenvalue of a matrix [12].

Joint convexity of matrix relative entropy

While the convexity with respect to \(A\) is straightforward, the relative entropy \(D(A \| B)\) is also jointly convex in \((A,B)\), which is crucial in the developments below. There exist several proofs, but one is particularly elegant [4] and will use the matrix-monotonicity that I presented in the last post.

Kronecker products. We need to make a clever use of Kronecker products. Given two matrices \(A\) and \(B\) of any sizes, \(A \otimes B\) is the matrix defined by blocks \(A_{ij} B\), thus of size the products of the number of rows and columns of \(A\) and \(B\). In the derivations below, both \(A\) and \(B\) will be of size \(d \times d\), and thus \(A \otimes B\) is then of size \(d^2 \times d^2\).

Kronecker products have very nice properties (they would probably deserve their own post!), such as (when dimensions are compatible), \((A \otimes B) ( C\otimes D) = (AC) \otimes (BD)\) or \((A \otimes B)^{\, -1} = A^{-1} \otimes B^{\, -1}\). What we will leverage is their use in characterizing linear operations on matrices. For a rectangular matrix \(X \in \mathbb{R}^{d_1 \times d_2}\), \({\rm vec}(X) \in \mathbb{R}^{d_1 d_2 \times 1}\) denotes the vectorization of \(X\) obtained by stacking all columns of \(X\) one after the other in a single column vector. Then, we have $$ (B^\top \otimes A){\rm vec}(X) = {\rm vec}(AXB)$$ for any \(A, X, B\) with compatible dimensions.

Reformulation of relative entropy. We can now use Kronecker products to get: $$ {\rm tr} [A \log A] = {\rm tr}[ A^{1/2}( \log A) A^{1/2} ] = {\rm vec}(A^{1/2})^\top [ I \otimes \log A ] {\rm vec}(A^{1/2}),$$ and $$ {\rm tr} [A \log B] = {\rm tr} [ A^{1/2}( \log B) A^{1/2} ] = {\rm vec}(A^{1/2})^\top [ \log B \otimes I ] {\rm vec}(A^{1/2}),$$ leading to $$D(A\|B) = {\rm vec}(A^{1/2})^\top \big[ I \otimes \log A \ – \log B \otimes I \big] {\rm vec}(A^{1/2}) \, – {\rm tr}(A) + {\rm tr}(B).$$ The key element is then to use the identity for PSD matrices $$\log(C \otimes D) = \log C \otimes I + I \otimes \log D$$ (which can be shown using the fact that eigenvalue decomposition of a Kronecker product of symmetric matrices can be obtained from the decompositions of the factors), leading to $$D(A\|B) = {\rm vec}(A^{1/2})^\top \big[ \log ( I \otimes A) \ – \log (B \otimes I) \big] {\rm vec}(A^{1/2})\, – {\rm tr}(A) + {\rm tr}(B).$$ It seems we have not achieved much, but now, the matrices \( I \otimes A\) and \(B \otimes I\) commute! Therefore, we can now write $$D(A\|B) = {\rm vec}(A^{1/2})^\top \Big[ \log \big( ( I \otimes A) (B \otimes I)^{-1} \big) \Big] {\rm vec}(A^{1/2})- {\rm tr}(A) + {\rm tr}(B).$$ This can then be rewritten as $$D(A\|B) =\, – {\rm vec}(A^{1/2})^\top \big[ \log ( B \otimes A^{-1}) \big] {\rm vec}(A^{1/2}) \, – {\rm tr}(A) + {\rm tr}(B).$$

Using matrix-convexity. We can now use the matrix-convexity of \(\lambda \mapsto \ – \log \lambda\), and the representation from last post as $$ -\log \lambda = 1-\lambda + (\lambda-1)^2 \int_0^{+\infty} \!\!\frac{1}{\lambda +u} \frac{du}{(1+u)^2},$$ leading to $$D(A\|B) = \int_0^{+\infty} {\rm vec}(A^{1/2})^\top \Big[ ( B\otimes A^{-1} – I)^2 (B\otimes A^{-1} + u I)^{-1} \Big] {\rm vec}(A^{1/2}) \frac{du}{(1+u)^2},$$ and then, by using \(( B\otimes A^{-1} – I) ( I \otimes A^{1/2}) {\rm vec}(A^{1/2}) = {\rm vec}(B-A)\), $$D(A\|B) = \int_0^{+\infty} {\rm vec}(A-B)^\top (B\otimes I+ u I \otimes A)^{-1} {\rm vec}(A-B) \frac{du}{(1+u)^2}.$$ We can then use the joint convexity of the function \((C,D) \mapsto {\rm tr} \big[ C^\top D^{-1} C \big] \) to get the joint convexity of \(D(A\|B)\).

This extends to all matrix-convex functions beyond the logarithm, such as \(\lambda \mapsto (\lambda-1)^2\), \(\lambda \mapsto 1 \, – \lambda^{1/2}\) or \(\displaystyle \lambda \mapsto \frac{1}{\lambda}(\lambda-1)^2\), leading to other \(f\)-divergences between matrices. See [5, Appendix A.4] for details.

Lieb concavity theorems

Now that \((A,B) \mapsto D(A\|B)\) is jointly convex on all PSD matrices (not only unit trace), for any fixed symmetric matrix \(M\), the function $$ \varphi: B \mapsto \sup_{ A \succcurlyeq 0} \ {\rm tr}(AM) + {\rm tr}(A) \ – D(A\|B), $$ as the partial maximization (with respect to \(B\)) of a jointly concave function of \((A,B)\), is concave. We can maximize in closed form with respect to \(A\) by computing the gradient \(M \ – \log A + \log B\), leading to \(A = \exp( M + \log B)\), and $$\varphi(B) = {\rm tr} \exp ( M + \log B),$$ which defines a concave function. This is one version of the classical Lieb concavity theorems [8].

As a consequence, we can obtain the “subadditivity of the matrix cumulant generative function”. That is, for any random independent symmetric matrices \(X_1,\dots,X_n\) of the same sizes, $$ \mathbb{E} \Big[ {\rm tr} \exp \big( \sum_{i=1}^n X_i \big) \Big] \leqslant {\rm tr} \exp \big( \sum_{i=1}^n \log \big( \mathbb{E} [ \exp( X_i ) ] \big),$$ which can be shown by recursion using Jensen’s inequality for the function \(\varphi\) above with a well-chosen matrix \(M\). See [2] for details.

We are now ready to consider concentration inequalities for random matrices.

Application to concentration inequalities

We consider random independent random matrices \(X_1,\dots,X_n\) such that \(\mathbb{E} [ X_i ] = 0\) for all \(i \in \{1,\dots,n\}\). Let \(S = \frac{1}{n} \sum_{i=1}^n \! X_i\) (which has zero mean). Our goal is to provide upper bounds on \(\mathbb{E} \big[ \lambda_{\max}(S) \big]\) and \(\mathbb{P} \big[ \lambda_{\max}(S) \geqslant t \big]\). We follow the outstanding work and presentation of Joel Tropp [2]: using the proper matrix tools presented above, we can get for matrix-valued random variables the almost exact same proofs of the usual concentration inequalities for real-valued random variables, such as Hoeffding, Bernstein, Azuma, or Mac-Diarmid inequalities.

Expectation. We have, for any \(u > 0\), by homogeneity of the largest eigenvalue: $$ \mathbb{E} \big[ \lambda_{\max}(S) \big] = \frac{1}{u} \mathbb{E} \big[ \lambda_{\max}(uS) \big] = \frac{1}{u} \mathbb{E} \big[ \log \exp ( \lambda_{\max}(uS) ) \big].$$ We can then use Jensen’s inequality for the logarithm to get (together with the fact the largest eigenvalue of the exponential is the exponential of the largest eigenvalue): $$ \mathbb{E} \big[ \lambda_{\max}(S) \big] \leqslant \frac{1}{u} \log \mathbb{E} \big[ \exp ( \lambda_{\max}(uS) ) \big]=\frac{1}{u} \log \mathbb{E} \big[ ( \lambda_{\max}( \exp ( uS) ) \big], $$ and finally that for a PSD matrix the trace is larger than the largest eigenvalue, to get $$ \mathbb{E} \big[ \lambda_{\max}(S) \big] \leqslant \frac{1}{u} \log \mathbb{E} \big[ {\rm tr} \exp ( uS ) \big].$$ Experts in concentration inequalities have probably recognized the usual argument to bound the expectation of the maximum of \(d\) random real-valued (non necessarily independent) variables \(X_1,\dots,X_d\), as $$ \mathbb{E} \big[ \max \{Y_1,\dots,Y_d\} \big] \leqslant \frac{1}{u} \log \mathbb{E} \big[ \exp(uY_1)+ \cdots + \exp(u Y_d) \big].$$

Tail bound. We have, using Markov’s inequality, for any \(u > 0\): $$\mathbb{P} \big[ \lambda_{\max}(S) \geqslant t \big] = \mathbb{P} \big[ \exp(\lambda_{\max}(uS)) \geqslant \exp(ut) \big] \leqslant e^{-ut} \mathbb{E} \big[ \exp ( \lambda_{\max}(uS) ) \big],$$ thus leading to $$\mathbb{P} \big[ \lambda_{\max}(S) \geqslant t \big] \leqslant e^{-ut} \mathbb{E} \big[ {\rm tr} \exp ( uS ) \big].$$ The same experts have recognized $$ \mathbb{P} \big[ \max \{Y_1,\dots,Y_d\} \geqslant t \big] \leqslant e^{-ut} \mathbb{E} \big[ \exp(uY_1)+ \cdots + \exp(u Y_d) \big].$$

We can now consider random matrices such that \(a I \preccurlyeq X_i \preccurlyeq b I\) almost surely for all \(i=1,\dots,n\) (and still with zero mean). We first need a lemma whose proof is given at the end of the post, with the exact same proof as for the uni-dimensional case.

Lemma. If \(\mathbb{E} [ X ] = 0\) and \(a I \preccurlyeq X \preccurlyeq b I\) almost surely, then for all \(u > 0\), $$ \mathbb{E} \big[ \exp( u X) \big] \preccurlyeq \exp\big( \frac{u^2}{8}(b-a)^2 \big) I.$$

Together with the consequence of Lieb’s result presented above and the matrix-monotonicity of the logarithm, we get: $$ \mathbb{E} \big[ {\rm tr} \exp ( uS ) \big] \leqslant {\rm tr} \exp \Big( n \big( \frac{u^2}{8n^2}(b-a)^2 I \big) \Big) = d \exp \big( \frac{u^2}{8n}(b-a)^2 \big).$$ We can then get immediately, by optimizing with respect to \(u\) (with optimal value \(u=4 n t /(b-a)^2\)), $$\mathbb{P} \big[ \lambda_{\max}(S) \geqslant t \big] \leqslant d \exp\big( – \frac{2 n t^2 }{(b-a)^2} \big),$$ and, with optimal value \(u= {2 \sqrt{2 n \log d }}/ { (b-a) }\): $$ \mathbb{E} \big[ \lambda_{\max}(S) \big] \leqslant \frac{b-a}{\sqrt{2n}} \sqrt{ \log d}.$$

Note that these are the exact same results as when \(d=1\)!

Extensions. As nicely detailed in [2], there are extensions to all classical concentration inequalities. Moreover, this can be applied to rectangular matrices, where the largest eigenvalue is replaced by the largest singular value. Finally, for those who like to work in infinite dimensions and cannot bear the explicit dependence in dimension, it is possible to derive results that depend only on a well-defined notion of “intrinsic dimension” (the associated results can then be used for the study of kernel methods, see [13, chapter 9]).

Conclusion

Now that we know everything about the matrix relative entropy and its convexity properties, we will explore next month a new link between eigenvalues of covariance operators and the regular Shannon entropy of the generating probability distribution [5], thus mixing my favorite recent mathematical topic with my probably all-time favorite one: positive definite kernels!

References

[1] Thomas M. Cover and Joy A. Thomas. Elements of Information Theory. John Wiley & Sons, 1999.
[2] Joel A. Tropp. An introduction to matrix concentration inequalities. Foundations and Trends in Machine Learning, 8(1-2):1–230, 2015.
[3] Yao-Liang Yu. The strong convexity of von Neumann’s entropy. Unpublished note, 2013.
[4] Mary Beth Ruskai. Another short and elementary proof of strong subadditivity of quantum entropy. Reports on Mathematical Physics, 60(1):1–12, 2007.
[5] Francis Bach. Information Theory with Kernel Methods. Technical Report, arXiv-2202.08545, 2022.
[6] Heinz H. Bauschke, and Jonathan M. Borwein. Joint and separate convexity of the Bregman distance. Studies in Computational Mathematics, 8:23-36, 2001.
[7] Martin J. Wainwright and Michael I. Jordan. Graphical Models, Exponential Families, and Variational Inference. Foundations and Trends in Machine Learning, 1 (1–2):1–305, 2008.
[8] Elliott H. Lieb. Convex trace functions and the Wigner-Yanase-Dyson conjecture.
Advances in Mathematics, 11(3):267–288, 1973.
[9] Stéphane Boucheron, Gabor Lugosi, and Pascal Massart. Concentration Inequalities: A Nonasymptotic Theory of Independence. Oxford University Press, 2013.
[10] Stephen Boyd, Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004.
[11] Anatoli Juditsky, Arkadi Nemirovski. First order methods for nonsmooth convex large-scale optimization, i: general purpose methods. Optimization for Machine Learning, 121-148, 2012.
[12] Yurii Nesterov. Smoothing technique and its applications in Semidefinite Optimization. Mathematical Programming, 110(2):245-259, 2007.
[13] Francis Bach. Learning Theory From First Principles. Book draft, 2021.

Proof of lemma on matrix cumulant generating functions

Lemma. If \(\mathbb{E} [ X ] = 0\) and \(a I \preccurlyeq X \preccurlyeq b I\) almost surely, then for all \(u > 0\), $$ \mathbb{E} \big[ \exp( u X) \big] \preccurlyeq \exp\big( \frac{u^2}{8}(b-a)^2 I \big) = \exp\big( \frac{u^2}{8}(b-a)^2 \big) I .$$ Note that we have \(a \leqslant 0 \leqslant b\).

Proof. We follow the standard proof [9] for real-valued random variables, simply transferred to the matrix case. On the interval \([a,b]\), by convexity of the exponential function $$ \exp(u\lambda) \leqslant \exp(ub) \frac{\lambda-a}{b-a} + \exp(ua) \frac{b \, – \lambda}{b-a}.$$ Thus (check why we can do this), almost surely: $$ \exp(uX) \preccurlyeq \exp(ub) \frac{X-a I }{b-a} + \exp(ua) \frac{bI – X}{b-a},$$ leading to \(\displaystyle \mathbb{E} [ \exp(uX) ] \preccurlyeq \frac{b \exp(ua)\ – a \exp(ub)}{b-a} I\). We can then show that \(\displaystyle \frac{b \exp(ua)\ – a \exp(ub)}{b-a} \leqslant \exp \Big( \frac{u^2}{8}(b-a)^2 \Big)\) to conclude the proof. We thus need to show that \(\displaystyle \psi(u) = \log \Big( \frac{b \exp(ua)\ – a \exp(ub)}{b-a} \Big) \leqslant \frac{u^2}{8}(b-a)^2\) for all \(u \geqslant 0\). We can simply express \(\psi(u)\) as a rescaled logistic function as $$\psi(u) = ua + \log \frac{b}{b-a} + \log\Big[ 1 + \exp\Big( u(b-a) + \log\frac{-a}{b-a} \Big) \Big].$$ We have \(\psi(0) = 0\), and $$\psi'(u) = \frac{ba \exp(ua)\ – ab \exp(ub)}{b \exp(ua)\ – a \exp(ub)}, $$ thus \(\psi'(0) = 0\), and through the link with the logistic function, the second-order derivarive is less than \((b-a)^2 / 4\). This leads to the desired result by Taylor’s formula.